Explication détaillée de la technologie de planification des décisions de conduite autonome

Avec le développement rapide de la technologie d'apprentissage par renforcement profond, de plus en plus d'équipes de recherche ont commencé à l'appliquer à la planification décisionnelle de conduite autonome, en intégrant des modules de prise de décision comportementale et de planification de mouvement pour apprendre directement les trajectoires de conduite.

Le module de planification décisionnelle en conduite autonome est l'un des indicateurs de base pour mesurer et évaluer les capacités de conduite autonome. Sa tâche principale est d'analyser l'environnement actuel après avoir reçu diverses informations sensorielles des capteurs, puis de contrôler le module de contrôle sous-jacent. ordres. Un module de planification décisionnelle typique peut être divisé en trois niveaux : planification du chemin global, prise de décision comportementale et planification des mouvements.

01 Introduction

Dans un système de conduite autonome complet, si le module de perception est comparé aux yeux et aux oreilles humains, alors la planification décisionnelle est le cerveau de la conduite autonome. Après avoir reçu diverses informations sensorielles du capteur, le cerveau analyse l'environnement actuel puis émet des instructions au module de contrôle sous-jacent. Ce processus constitue la tâche principale du module de prise de décision et de planification. Dans le même temps, la complexité des scénarios que le module de planification décisionnelle peut gérer est également l’un des indicateurs clés pour mesurer et évaluer les capacités de conduite autonome [1].

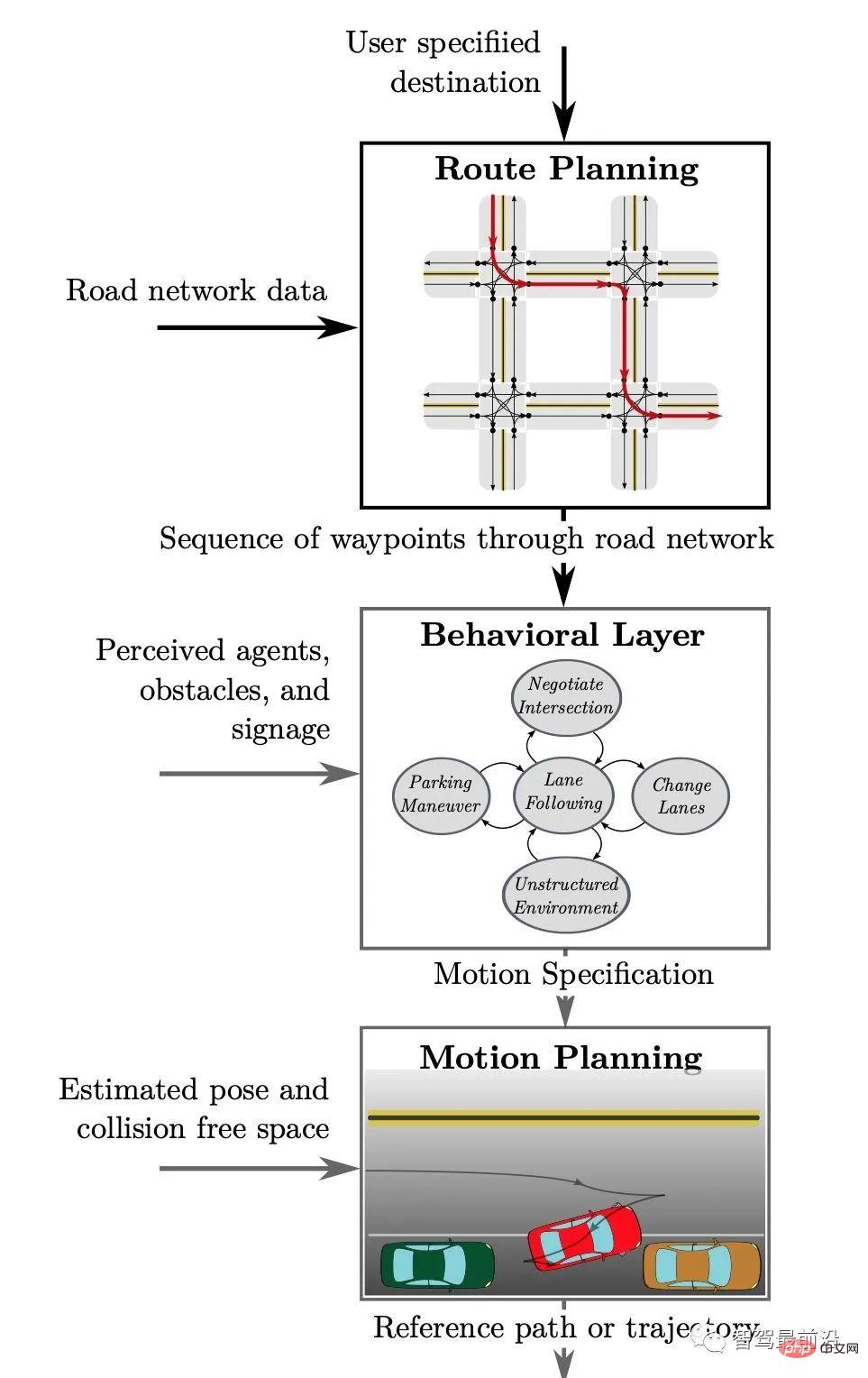
Figure 1. La structure hiérarchique du module de planification décisionnelle dans le système de conduite autonome, citée dans [2]

Comme le montre la figure 1, un module de planification décisionnelle typique peut être divisé en trois niveaux .

Parmi eux, après avoir reçu une destination de conduite donnée, la planification d'itinéraire globale (Route Planning) combine les informations cartographiques pour générer un itinéraire global comme référence pour la planification d'itinéraire spécifique ultérieure.

Couche comportementale) Après avoir reçu le chemin global, combinez ; les informations environnementales obtenues à partir du module de perception (y compris les autres véhicules et piétons, les obstacles et les informations sur les règles de circulation sur la route) pour prendre des décisions comportementales spécifiques (comme choisir de changer de voie pour dépasser ou suivre

Enfin, la planification des mouvements) ; La couche prévoit de générer une trajectoire qui satisfait des contraintes spécifiques (telles que les propres contraintes dynamiques du véhicule, l'évitement des collisions, le confort des passagers, etc.) sur la base de décisions comportementales spécifiques. Cette trajectoire sert d'entrée au module de contrôle pour déterminer le chemin de déplacement final du véhicule.

Cet article présentera respectivement les principales fonctions et les algorithmes communs de chaque couche, et comparera les avantages et les inconvénients de divers algorithmes et scénarios applicables.

02 Planification globale du chemin (Planification d'itinéraire)

La planification globale du chemin fait référence à la sélection d'un chemin optimal via la recherche après avoir donné la position actuelle du véhicule et la cible finale. Le « optimal » inclut ici le chemin le plus court ou l'heure d'arrivée. Conditions les plus rapides et autres. Ce processus est similaire à la fonction « navigation » que nous utilisons souvent dans nos vies. La différence est que la carte de haute précision utilisée dans la conduite autonome est différente de nos cartes communes. La carte de haute précision contient plus d'informations sur chaque voie. information. Les algorithmes courants de planification de chemin global incluent les algorithmes de Dijkstra et A, ainsi que diverses améliorations basées sur ces deux algorithmes. L'algorithme de Dijkstra [3] et l'algorithme A* [4] sont également les deux algorithmes de recherche les plus largement utilisés dans de nombreux problèmes de planification.

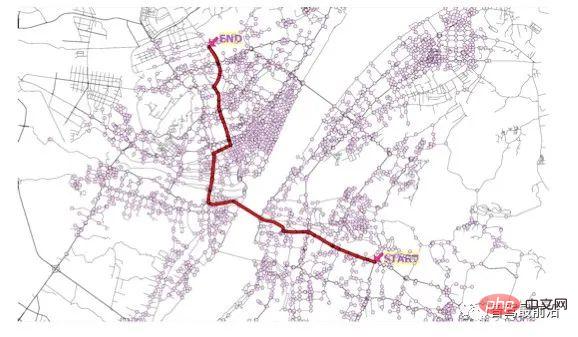
Figure 2. Schéma de la planification globale du chemin

1. Algorithme de Dijkstra

L'algorithme de Dijkstra a été proposé par l'informaticien Edsger W. Dijkstra en 1956 pour trouver le chemin le plus court entre les nœuds d'un graphique. Dans l'algorithme de Dijkstra, le coût total de déplacement de chaque nœud depuis le point de départ doit être calculé. Dans le même temps, une structure de file d’attente prioritaire est également nécessaire. Tous les nœuds à parcourir seront triés en fonction du coût lorsqu'ils seront placés dans la file d'attente prioritaire. Pendant l'exécution de l'algorithme, le nœud ayant le coût le plus faible est sélectionné à chaque fois dans la file d'attente prioritaire comme prochain nœud traversé. jusqu'à ce que vous atteigniez la fin.

L'avantage de l'algorithme de Dijkstra est que le chemin donné est optimal ; l'inconvénient est que la complexité du temps de calcul est relativement élevée (O(N2)), car il explore les environs sans direction claire.

2. Algorithme A*

Afin de résoudre le problème d'efficacité de recherche de l'algorithme de Dijkstra, en 1968, l'algorithme A a été publié par Peter Hart, Nils Nilsson et Bertram Raphael du Stanford Research Institute. Sa principale amélioration est d'utiliser. une fonction heuristique pour guider le processus de recherche. Plus précisément, l'algorithme A calcule la priorité de chaque nœud grâce à la fonction suivante :

f(n)=g(n)+h(n)

où :

• f(n) est la priorité globale du nœud n. Lorsque nous sélectionnons le prochain nœud à parcourir, nous sélectionnons toujours le nœud avec la priorité globale la plus élevée (valeur minimale).
• g(n) est le coût du nœud n à partir du point de départ.
• h(n) est le coût estimé du nœud n à partir du point final, qui est la fonction heuristique de l'algorithme A*.

03 Couche comportementale

Après avoir déterminé la trajectoire globale, le véhicule autonome doit prendre des décisions comportementales appropriées en fonction des conditions routières spécifiques, des règles de circulation, des autres véhicules et des piétons.

Ce processus est confronté à trois problèmes principaux :

Premièrement, les scènes de conduite réelles sont en constante évolution, comment les couvrir ?

Deuxièmement, la scène de conduite réelle est un environnement de prise de décision multi-agents. Le comportement de chaque participant, y compris le véhicule principal, aura un impact sur les autres participants de l'environnement, nous devons donc prédire le comportement des autres participants.

Enfin, il est impossible pour les véhicules autonomes d'atteindre une perception à 100 % des informations environnementales. Par exemple, il existe de nombreuses situations dangereuses possibles qui sont bloquées par des obstacles.

Sur la base des points ci-dessus, dans la couche décisionnelle relative au comportement de conduite autonome, ce que nous devons résoudre est le problème de planification de l'incertitude perceptuelle dans l'environnement complexe de la prise de décision multi-agents. On peut dire que ce problème est l'un des principaux goulots d'étranglement dans la réalisation véritable d'une technologie de conduite autonome de niveau L4 et L5. Ces dernières années, avec le développement rapide de l'apprentissage par renforcement profond et d'autres domaines, de nouvelles idées et de nouvelles idées ont été apportées pour résoudre ce problème. problème.

Les modèles de la couche de prise de décision comportementale sont divisés en quatre catégories et présentés ci-dessous [5] :

1. Modèle de machine à états finis

Le modèle de prise de décision initial des véhicules autonomes est le modèle de machine à états finis. [6] Le véhicule est basé sur la sélection de comportements de conduite appropriés dans l'environnement actuel, tels que le stationnement, le changement de voie, le dépassement, l'évitement, la conduite lente, etc. Le modèle de machine à états décrit différents états de conduite et les relations de transfert entre les états en construisant un graphique connecté orienté limité, qui génère ainsi, en fonction de la transition de l'état de conduite, des actions de conduite de manière réactive.

Le modèle de machine à états finis est actuellement le modèle de prise de décision comportementale le plus répandu dans le domaine de la conduite autonome en raison de sa simplicité et de sa facilité de mise en œuvre. Cependant, ce type de modèle ignore la dynamique et l'incertitude de l'environnement. lorsque la scène de conduite présente de nombreuses caractéristiques, la division et la gestion de l'État sont relativement lourdes, conviennent principalement à des scénarios simples et sont difficiles à effectuer des tâches de prise de décision comportementale dans des environnements routiers urbains présentant de riches caractéristiques structurelles.

2. Modèle d'arbre de décision

Le modèle d'arbre de décision/comportement [7] est similaire au modèle de machine à états, il sélectionne également différentes actions de conduite de manière réactive via les valeurs d'attribut de l'état de conduite actuel, mais. la différence est que ce type de modèle Le statut de conduite et la logique de contrôle sont solidifiés dans une structure arborescente, et la recherche de stratégie de conduite est effectuée via un mécanisme de « sondage » descendant. Ce type de modèle de prise de décision a une logique de contrôle visuel et les nœuds de contrôle peuvent être réutilisés, mais il doit définir le réseau de prise de décision hors ligne pour chaque scénario de conduite. Lorsque l'espace d'état et l'espace de comportement sont grands, la logique de contrôle le fera. être plus complexe. De plus, ce type de modèle est également incapable de prendre en compte les facteurs d’incertitude existant dans l’environnement du trafic.

3. Modèle de raisonnement et de prise de décision basé sur la connaissance

Le modèle de raisonnement et de prise de décision basé sur la connaissance imite le processus de prise de décision comportementale des conducteurs humains par la relation cartographique des « caractéristiques de la scène-actions de conduite ». Ce type de modèle stocke les connaissances de conduite dans les connaissances. Dans une bibliothèque ou un réseau de neurones, les connaissances de conduite sont ici principalement représentées par la relation de mappage entre les règles, les cas ou les caractéristiques de la scène et les actions de conduite. Ensuite, les actions de conduite sont déduites de la base de connaissances ou de la structure du réseau formé via le mécanisme de « requête ».

Ce type de modèle comprend principalement : un système de raisonnement basé sur des règles [8], un système de raisonnement basé sur des cas [9] et un modèle de cartographie basé sur un réseau neuronal [10].

Ce type de modèle repose fortement sur les connaissances de conduite préalables et les données de formation, et nécessite une organisation, une gestion et une mise à jour minutieuses des connaissances de conduite. Bien que le modèle de cartographie basé sur les réseaux neuronaux puisse économiser le processus d'annotation des données et d'intégration des connaissances, il existe. il existe toujours les lacunes suivantes :

• Son mécanisme basé sur les "données" le rend fortement dépendant des données de formation, et les données de formation doivent être suffisantes [11]
• La relation de cartographie est solidifiée dans la structure du réseau et son interprétabilité est médiocre ;
• Il existe un problème de « boîte noire », une mauvaise transparence, une mauvaise traçabilité des problèmes qui surviennent dans le système réel et il est difficile de trouver la cause profonde du problème.

4. Modèle de prise de décision basé sur la valeur

Selon la théorie de l'utilité maximale, l'idée de base du modèle de prise de décision basé sur l'utilité/la valeur est de sélectionner la stratégie/action de conduite optimale parmi plusieurs alternatives basées sur les critères de sélection[ 12].

Afin d'évaluer la qualité de chaque action de conduite, ce type de modèle définit une fonction d'utilité (utilité) ou de valeur (valeur) pour évaluer quantitativement le degré dans lequel la stratégie de conduite répond à l'objectif de la tâche de conduite en fonction de certains attributs de critères. tâches de conduite autonome Plus précisément, ces attributs de critère peuvent être la sécurité, le confort, l'efficacité de conduite, etc., et l'utilité et la valeur peuvent être déterminées par un seul attribut ou plusieurs attributs.

Furda et Vlacic de l'Université Griffith en Australie ont proposé une méthode de prise de décision multicritère pour sélectionner l'action de conduite optimale parmi l'ensemble d'actions candidates [13] de l'Université nationale de Singapour ont proposé une prise de décision comportementale ; modèle basé sur POMDP [14], pour résoudre les situations où il existe une incertitude perçue ; Wei J et d'autres de l'Université Carnegie Mellon ont proposé un modèle de prise de décision comportementale basé sur PCB (Prediction and-Cost-function Based) [15], qui se concentre sur la manière de construire une fonction de coût appropriée pour guider la prédiction de l'environnement afin de résoudre le problème de prise de décision dans des environnements complexes impliquant plusieurs agents, de nombreux modèles basés sur la théorie des jeux sont également utilisés par les chercheurs pour raisonner sur la comportement interactif entre les véhicules [16], [17 ] De plus, en raison de ses avantages dans l'extraction de caractéristiques, la technologie d'apprentissage par renforcement profond a également commencé à être largement utilisée pour compléter la génération d'actions de conduite optimales [18].

04 Planification de mouvement

Après avoir déterminé le comportement de conduite spécifique, ce que nous devons faire est de transformer le "comportement" en une "trajectoire" de conduite plus spécifique, afin que nous puissions enfin générer une série de contrôles spécifiques sur le signal du véhicule pour réaliser la conduite du véhicule selon l'objectif prévu. Ce processus est appelé planification de mouvement. Le concept de planification de mouvement a une longue histoire de recherche dans le domaine de la robotique. D'un point de vue mathématique, nous pouvons le considérer comme le problème d'optimisation suivant :

Planification de chemin (Path Planning)

.

Figure 3. Définition de la planification de chemin

Dans de nombreux scénarios représentés par des robots, nous pouvons considérer l'environnement environnant comme déterministe. Dans ce cas, ce qu'on appelle la planification de chemin fait référence à la recherche d'une cartographie σ:[0,1]➞Χ qui satisfait certaines contraintes dans un espace d'état donné Χ. Ces contraintes incluent :

• point de départ déterminé L'état initial et le. zone où se trouve le point cible
• Éviter les collisions
• Contraintes différentielles sur le chemin (par exemple, dans des problèmes réels, la courbure du chemin ne peut pas être trop petite, correspondant aux contraintes de sa dérivée seconde)

La fonctionnelle objective de le problème d'optimisation Il est défini comme J(σ) et sa signification spécifique peut être exprimée sous forme de normes de mesure telles que la longueur du trajet et la complexité du contrôle.

Cependant, dans le problème de la conduite automatique, l'environnement autour du véhicule change constamment de manière dynamique, donc une simple planification de trajet ne peut pas donner une solution qui soit toujours valable pendant le processus de conduite, nous devons donc ajouter une dimension - le temps T, la planification correspondante Le problème est souvent appelé planification de trajectoire.

Planification de trajectoire

Figure 4. Définition de la planification de trajectoire

L'augmentation de la dimension temporelle apporte d'énormes défis au problème de planification. Par exemple, pour un robot se déplaçant dans un environnement 2D, abstrait sous la forme d’un seul point, les obstacles de l’environnement sont approximés sous forme de polygones. Le problème de planification de trajectoire peut être résolu en temps polynomial, tandis que le problème de planification de trajectoire qui ajoute la dimension temporelle s'est avéré être un problème NP-difficile.

Dans le scénario actuel de la conduite autonome, qu'il s'agisse du véhicule lui-même ou de son environnement, l'établissement d'un modèle plus précis signifie des contraintes plus complexes sur le problème d'optimisation, et cela signifie également que la solution est plus difficile. Par conséquent, les algorithmes réellement utilisés sont basés sur le principe d’une approximation de la scène réelle et recherchent un équilibre optimal entre la précision du modèle et l’efficacité de la solution.

Ce qui suit présente plusieurs types courants d'algorithmes de planification de mouvement actuellement dans le domaine de la conduite autonome. Dans la pratique, c'est souvent la combinaison de plusieurs types d'idées qui permet finalement d'obtenir de meilleurs résultats de planification et de satisfaire davantage de scénarios différents.

1. Algorithme de planification basé sur la recherche

Résoudre les problèmes de planification de mouvement via la recherche est l'une des idées les plus simples. L'idée de base est de discrétiser l'espace d'état dans un graphique d'une certaine manière, puis d'utiliser divers algorithmes de recherche heuristiques. recherche de solutions réalisables voire de solutions optimales.​​

Dans le processus de discrétisation de l'espace d'état, il convient de veiller à ce que la grille finale ait la plus grande zone de couverture et ne se répète pas. Comme le montre la figure 5, la grille de gauche est générée par trois comportements : aller tout droit, tourner à gauche de 90° et tourner à droite de 90° et si vous choisissez trois comportements : aller tout droit, tourner à gauche de 89° et tourner à droite de 89° ; °, vous ne pourrez pas Générer une structure de grille couvrant toute la zone.

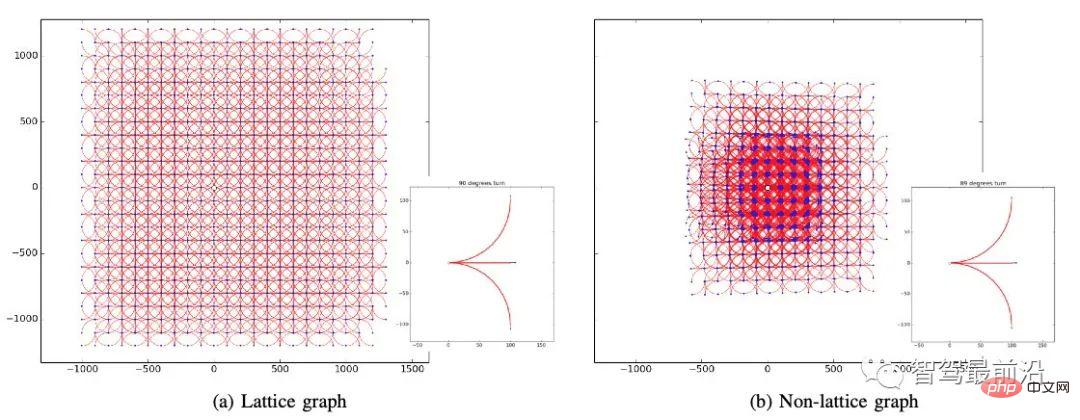
Figure 5. Construction d'un graphe raster, cité dans [2]

Après avoir rastérisé l'espace d'état, nous pouvons utiliser les algorithmes de recherche Dijkstra et A* déjà introduits ci-dessus pour terminer la planification finale. Cependant, dans les environnements complexes réels, il existe de nombreuses grilles et l'environnement change dynamiquement au fil du temps, ce qui entraînera un trop grand nombre de nœuds de recherche. Par conséquent, une variété d'algorithmes améliorés ont été développés pour traiter différents scénarios spécifiques :

1) Hybride. L'algorithme A*, basé sur l'algorithme A*, considère le problème de direction maximale du véhicule, par exemple en limitant la direction de direction maximale du véhicule sur la trajectoire calculée à pas plus de 5°. Les scénarios d'application actuels de cet algorithme incluent les demi-tours de voiture (la voiture Junior utilisée par Stanford pour participer au défi DARPA a utilisé cet algorithme pour effectuer un demi-tour), le stationnement et d'autres scénarios nécessitant un contrôle élevé du volant.

2) Algorithmes D* et D*Lite, recherchez à l'avance du point final au point de départ, utilisez l'algorithme de Dijkstra pour stocker la longueur de chemin la plus courte k du point cible à chaque point du réseau routier, et le chemin réel la valeur de longueur du nœud au point cible h, dans le cas initial k == h, et le nœud précédent de chaque nœud est stocké pour garantir que le lien peut être suivi.

Une fois le calcul terminé, un chemin optimal à ce moment-là est obtenu. Lorsque la voiture se dirige vers un certain nœud, le capteur détecte que le nœud est infranchissable (il y a des obstacles), puis la valeur h de certains points pertinents dans les informations stockées sur le réseau routier est modifiée (augmentée) et un point voisin est sélectionné qui satisfait toujours au problème h==k, c'est-à-dire que le point sur le chemin optimal est toujours le point suivant.

Ensuite, marchez jusqu'au bout. Ce type d'algorithme est adapté à la navigation et à la planification de trajectoires dans des environnements inconnus, et est largement utilisé dans divers robots mobiles et véhicules autonomes actuels, tels que les rovers martiens « Opportunity » et « Spirit ».

2. L'algorithme de planification basé sur l'échantillonnage

approxime le problème d'origine en un problème d'optimisation de séquence discrète en échantillonnant l'espace d'états continu. Cette idée est également l'algorithme le plus largement utilisé en informatique. Dans les problèmes de planification de mouvement, les algorithmes de base basés sur l'échantillonnage incluent les algorithmes Probabilistic Roadmap (PRM) et Rapid Search Random Tree (RRT).

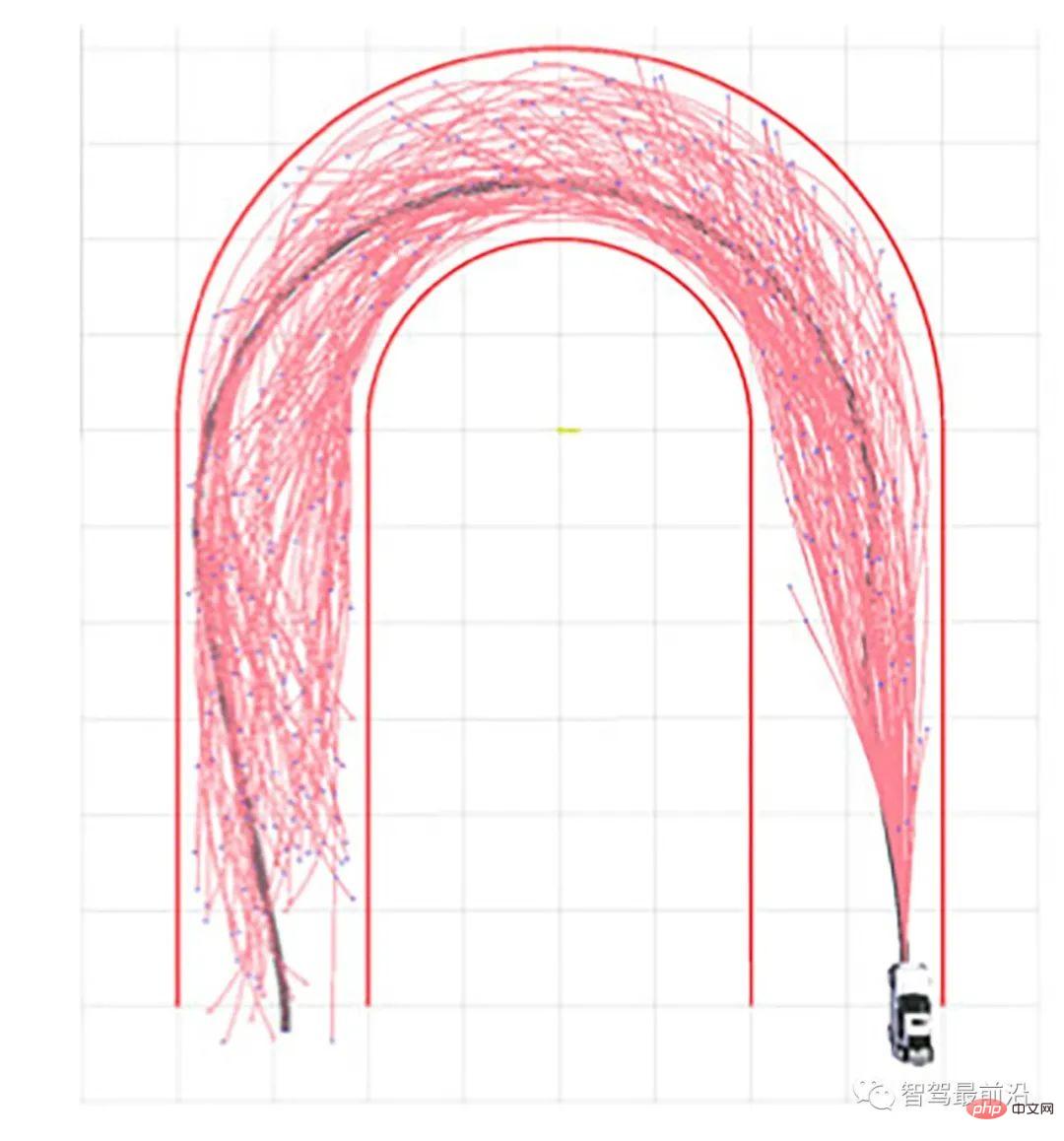
Figure 6. Planification d'une trajectoire de virage en forme de U à l'aide de l'algorithme RRT, cité dans [19]

1) Algorithme de base : Feuille de route probabiliste (PRM)

• Étape de prétraitement : l'espace d'état n points sont uniformément et échantillonné de manière aléatoire dans la zone de sécurité au sein du réseau, et chaque point d'échantillonnage est connecté à des points d'échantillonnage adjacents à une certaine distance, et les trajectoires qui entrent en collision avec des obstacles sont rejetées, et un graphique connecté est finalement obtenu.
• Phase de requête : pour une paire donnée d'états initial et cible, connectez-les au graphe déjà construit, puis utilisez l'algorithme de recherche pour trouver une trajectoire qui répond aux exigences.

Il est facile de voir qu'une fois qu'un PRM est construit, il peut être utilisé pour résoudre des problèmes de planification de mouvement dans différents états initiaux et cibles, mais cette fonctionnalité n'est pas nécessaire pour la planification de mouvement de conduite autonome. De plus, le PRM nécessite des connexions précises entre les états, ce qui est très difficile pour les problèmes de planification de mouvement avec des contraintes différentielles complexes.

2) Algorithme de base : Arbre aléatoire de recherche rapide (RRT)

• Initialisation de l'arbre : Initialise l'ensemble de nœuds et l'ensemble de bords de l'arbre. L'ensemble de nœuds contient uniquement l'état initial et l'ensemble de bords est vide. .
• Croissance de l'arbre : échantillonnez aléatoirement l'espace d'états. Lorsque le point d'échantillonnage se trouve dans la zone sûre de l'espace d'états, sélectionnez le nœud le plus proche du point d'échantillonnage dans l'arbre actuel et développez (ou connectez-le) au point d'échantillonnage. . Si la trajectoire générée n'entre pas en collision avec des obstacles, la trajectoire est ajoutée à l'ensemble de bords de l'arbre et le point final de la trajectoire est ajouté à l'ensemble de nœuds de l'arbre.

RRT est une méthode de recherche d'échantillonnage incrémentielle qui ne nécessite la définition d'aucun paramètre de résolution. Dans le cas extrême, l'arbre de recherche couvrira de manière dense tout l'espace. À ce stade, l'arbre de recherche est composé de nombreuses courbes ou chemins plus courts pour atteindre l'objectif de remplir tout l'espace.

3) Divers algorithmes améliorés

D'après la description de l'algorithme de base ci-dessus, nous pouvons comprendre que l'échantillonnage de l'espace d'état peut garantir une solution réalisable reliant le point de départ et le point final, mais puisque le processus d'échantillonnage est effectué sur l'ensemble de l'espace Échantillonnage uniforme, l'efficacité est donc très faible ; une solution en temps réel ne peut pas être obtenue dans des scénarios complexes. De plus, le résultat final de la planification ne peut pas garantir que la solution réalisable obtenue est la solution optimale ; En réponse à ces inconvénients, une variété d'algorithmes améliorés ont été proposés et appliqués aux problèmes de conduite autonome :

• Amélioration de l'efficacité --échantillonnage inégal

- RRT-Connect : construisez simultanément deux arbres à partir de l'état initial et de la cible Dans cet état, lorsque deux arbres poussent ensemble, une solution réalisable est trouvée.

- Heuristique (hRRT) : utilisez une fonction heuristique pour augmenter la probabilité que les nœuds à faibles coûts d'expansion soient échantillonnés.

- Combiné avec le modèle du conducteur : combiné avec le modèle d'attention visuelle du conducteur pour un échantillonnage biaisé, les informations sur les caractéristiques visuelles sont utilisées pour guider la planification des mouvements, afin que la trajectoire planifiée soit plus cohérente avec le comportement de conduite humain.

- Construire une nouvelle métrique RG-RRT (accessability guidée RT) : la métrique de distance euclidienne conventionnelle ne peut pas vraiment refléter la distance entre les configurations ou les états. RG-RRT calcule l'ensemble d'accessibilité des nœuds dans l'arborescence. la distance jusqu'à un nœud est supérieure à la distance accessible entre le point d'échantillonnage et le nœud, le nœud peut être sélectionné pour une expansion.

- Ajouter une pénalité d'obstacle (RC-RRT, EG-RRT, ADD-RRT, etc.) : Réduisez la probabilité que les nœuds proches des obstacles soient étendus.

• Amélioration en temps réel

- à tout moment, RRT construit d'abord rapidement un RRT, obtient une solution réalisable et enregistre son coût. Ensuite, l'algorithme continuera l'échantillonnage, mais insérera uniquement les nœuds dans l'arborescence qui sont bénéfiques pour réduire le coût. de la solution réalisable, obtenant ainsi progressivement de meilleures solutions réalisables.

- La replanification décompose l'ensemble de la tâche de planification en un certain nombre de séquences de sous-tâches de même durée et planifie la tâche suivante tout en exécutant la tâche en cours.

• Amélioration de l'optimalité

- PRM*, RRG, RRT* : selon la théorie des graphes géométriques aléatoires (échantillonnage aléatoire de m points dans l'espace d'état et connexion des points avec une distance inférieure à r(n), il forme Random graphiques géométriques) ont été améliorés sur les algorithmes PRM et RRT standards, et les algorithmes PRM*, RRG et RRT* avec des propriétés asymptotiques optimales ont été obtenus

3 Méthode d'optimisation directe

Dans la plupart des cas, elle ne prend pas en compte les changements d'altitude. , le problème de planification de trajectoire de la conduite autonome est un problème d'optimisation contrainte tridimensionnelle (espace 2D + temps T). Par conséquent, nous pouvons utiliser une stratégie de découplage pour décomposer le problème d'origine en plusieurs problèmes de faible dimension, réduisant ainsi considérablement le problème de. résoudre le problème.

1) Système de coordonnées Frenet

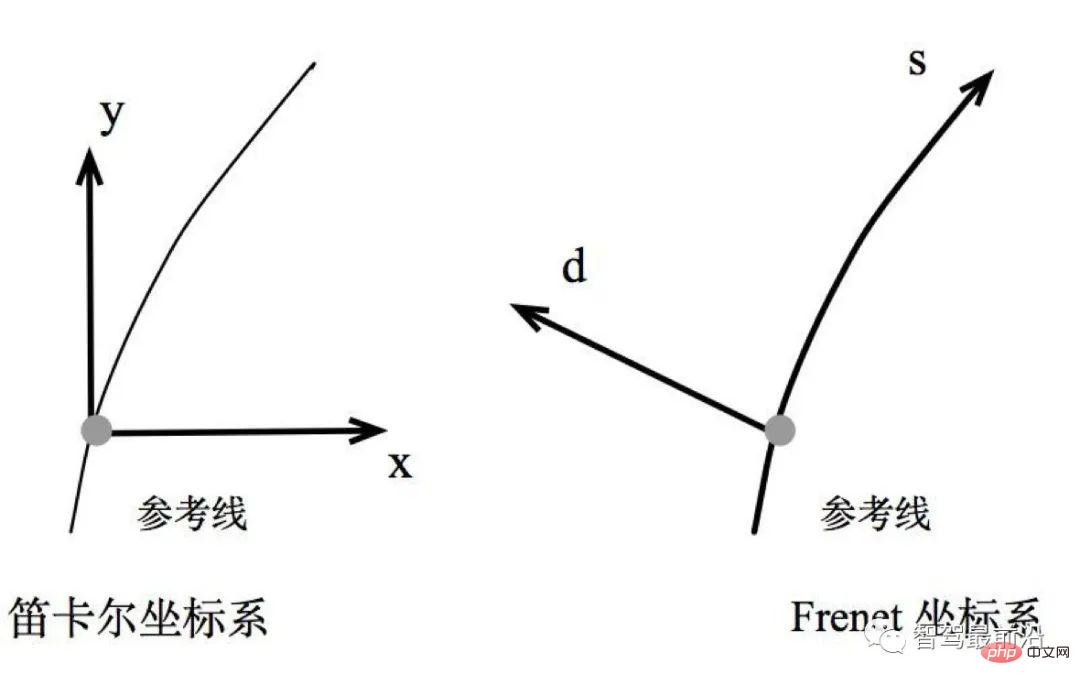
Figure 7. Système de coordonnées Frenet

Étant donné que les routes du monde réel sont courbes, afin de simplifier l'expression des paramètres de la résolution des problèmes d'optimisation, Frenet est généralement utilisé dans système de coordonnées de conduite autonome.

Dans le système de coordonnées Frenet, nous utilisons la ligne médiane de la route comme ligne de référence, et utilisons le vecteur tangent t et le vecteur normal n de la ligne de référence pour établir un système de coordonnées, comme le montre l'image de droite, qui prend le véhicule lui-même comme origine et l'axe de coordonnées perpendiculaires l'un à l'autre, il est divisé en direction s (c'est-à-dire la direction le long de la ligne de référence, généralement appelée longitudinale, longitudinale) et direction d (ou direction L, c'est-à-dire , la direction normale actuelle de la ligne de référence, appelée transversale, latérale). Par rapport au système de coordonnées cartésiennes (image de gauche), le système de coordonnées Frenet simplifie considérablement le problème.

Parce que lorsque nous conduisons sur route, nous pouvons toujours trouver facilement la ligne de référence de la route (c'est-à-dire la ligne médiane de la route), alors la position basée sur la ligne de référence peut simplement être exprimée en utilisant la distance longitudinale S (c'est-à-dire , dans la direction de la route) et la distance latérale L (c'est-à-dire la distance par rapport à la ligne de référence).

2) Méthode de découplage chemin-vitesse

Dans le système de coordonnées Frenet, la méthode de découplage chemin-vitesse optimise respectivement le chemin et la vitesse. L'optimisation du chemin prend principalement en compte les obstacles statiques et génère un chemin de référence statique grâce à une planification dynamique (. dimension SL), puis en fonction du chemin généré, envisager la planification de la vitesse (dimension ST). Ce processus peut être itéré en continu, permettant des mises à jour en temps réel de la trajectoire. Le planificateur EM utilisé dans la plateforme de conduite autonome open source Apollo de Baidu est basé sur une solution similaire. Cette solution présente une grande flexibilité et peut être appliquée universellement à de nombreux scénarios.

De plus, vous pouvez également choisir différentes méthodes de découplage, telles que la planification séparée de la trajectoire longitudinale (dimension ST) et de la trajectoire transversale (dimension LT). Cependant, il convient de souligner que la solution obtenue grâce à la méthode de découplage peut ne pas être optimale, que cet algorithme n'est pas complet et qu'une solution réalisable peut ne pas être trouvée dans certains environnements complexes.

4. Méthode de construction de courbe paramétrique

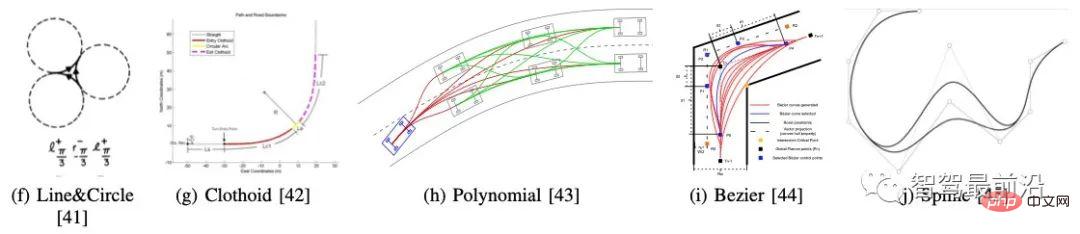
Figure 8. Méthode de construction de courbe paramétrique courante, citée dans [19]

Le point de départ de la méthode de construction de courbe paramétrique sont les contraintes du véhicule lui-même, y compris la cinématique Il existe des contraintes sur la dynamique, de sorte que la trajectoire généralement planifiée doit avoir une courbure continue. Ce type de méthode considère les obstacles en fonction du point de départ et du point cible, et donne un chemin fluide en construisant une famille de courbes conformes aux contraintes du véhicule.

Comme le montre la figure 8, les courbes courantes incluent la courbe de Dubins (constituée de lignes droites et d'arcs, qui est la famille de courbes la plus courte d'un modèle de véhicule simple, le modèle de Dubin dans un espace bidimensionnel), la courbe Clothoïde, la courbe polynomiale et la courbe de Bézier. , cannelures, etc. Il est difficile d'appliquer simplement la méthode de construction de courbes paramétriques pour répondre à des scénarios complexes réels. Par conséquent, de plus en plus de systèmes de conduite autonome la combinent désormais avec d'autres méthodes pour lisser les trajectoires planifiées et générées afin de satisfaire les contraintes cinématiques et dynamiques du véhicule.

5. Méthode du champ de potentiel artificiel

La méthode du champ potentiel artificiel s'inspire du champ électromagnétique en physique. On suppose que les obstacles et les positions cibles génèrent respectivement de la répulsion et de la gravité, de sorte que le chemin puisse être planifié le long de la descente la plus rapide du champ potentiel. Un problème clé dans ce type de méthode est de savoir comment sélectionner une fonction de champ potentiel appropriée. Par exemple, Stephen Waydo utilise des fonctions de flux pour une planification fluide des trajectoires [20], et Robert Daily propose une méthode de planification de trajectoire de champ potentiel harmonique sur les véhicules à grande vitesse. [21]. Dans des scénarios simples, la méthode du champ de potentiel artificiel a une efficacité de solution élevée, mais son plus gros problème est qu'elle peut tomber dans un minimum local. Dans ce cas, le chemin obtenu n'est pas optimal et le chemin peut même ne pas être trouvé.

05 Complexité de l'algorithme (Complexité)

Dans les problèmes de planification, en plus de considérer sa complexité temporelle et spatiale, l'évaluation d'un algorithme doit également déterminer s'il est complet et optimal. Prendre du recul Ensuite, déterminer s'il est probabiliste. exhaustivité et optimalité asymptotique. Ce n'est que sur la base de la compréhension de ces propriétés que nous pouvons concevoir et appliquer différents algorithmes pour différents scénarios réels, afin d'atteindre le meilleur équilibre entre complexité du modèle et efficacité optimale.

1) Complétude : S'il existe une solution de chemin entre le point de départ et le point cible, alors la solution doit être obtenue. Si la solution ne peut pas être obtenue, cela doit signifier qu'il n'y a pas de solution

2) Complétude probabiliste ; ) : S'il existe une solution de chemin entre le point de départ et le point cible, tant que le temps de planification ou de recherche est suffisamment long, il sera sûr de trouver une solution de chemin

3) Optimalité : Le chemin prévu est à l'intérieur ; Il est optimal sur un certain indice d'évaluation (l'indice d'évaluation est généralement la longueur du chemin)

4) Optimalité asymptotique : le chemin obtenu après un nombre limité d'itérations de planification est un chemin sous-optimal proche de l'optimal, et après à chaque itération, il se rapproche du chemin optimal, qui est un processus de convergence progressif

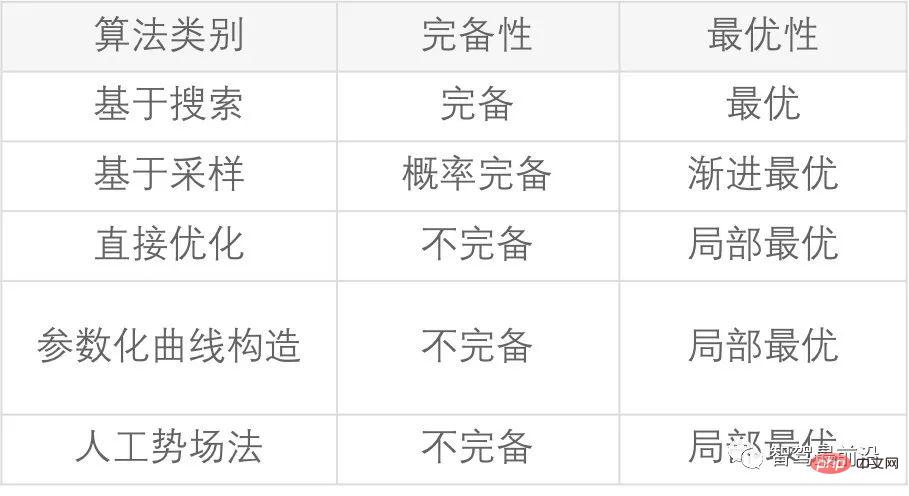
Tableau 1 Comparaison des algorithmes courants

06 Tendances de développement futures

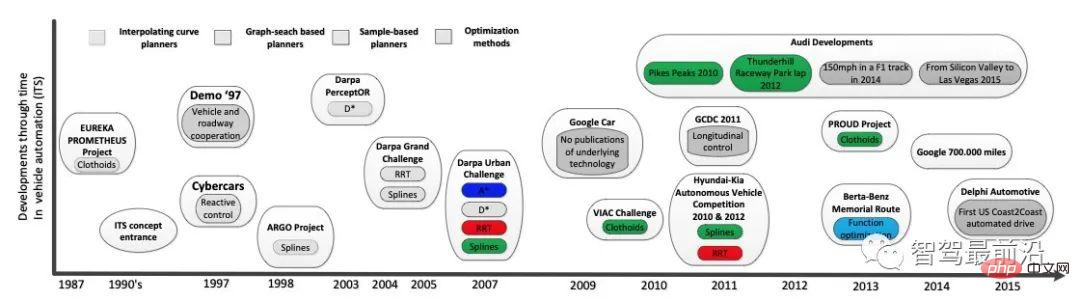
Figure 9. Chronologie et processus de développement de la conduite autonome Mouvement important algorithme de planification, cité dans [19]

L'intérêt humain pour la conduite autonome remonte à 1925. Ces dernières années, le boom de la recherche sur la conduite autonome a commencé avec l'Agence américaine des projets de recherche avancée de défense (DARPA) qui a posé trois défis de conduite autonome. de 2004 à 2007 [22], comme le montre la figure 9. Par la suite, l’efficacité des différentes méthodes de planification décisionnelle mentionnées ci-dessus a été effectivement vérifiée. Dans le même temps, des solutions combinant les méthodes de planification de mouvement avec la théorie du contrôle, l'estimation des paramètres d'état, l'apprentissage automatique et d'autres méthodes multi-domaines continuent d'émerger, devenant une tendance de développement future :

1) Combinaison avec la dynamique du véhicule : évaluation des paramètres dynamiques. indicateurs avec une planification optimale, la planification dans la perspective d'un contrôle optimal est une méthode qui a été davantage utilisée ces dernières années. Dans ce processus, les facteurs dynamiques du véhicule peuvent être pleinement pris en compte et la trajectoire planifiée est plus raisonnable. Par exemple, utilisez la théorie du contrôle prédictif des modèles (Model Predictive Control). L'inconvénient est que plus il y a de contraintes sur le véhicule, plus il est difficile d'optimiser sa trajectoire, et plus il est difficile de réaliser un calcul en ligne et en temps réel.

2) Combiné avec l'estimation des paramètres d'état : l'estimation des paramètres d'état peut obtenir les paramètres du véhicule avec plus de précision, de sorte que l'estimateur d'état peut être ajouté au module de planification pour améliorer la qualité de la trajectoire en estimant l'état du véhicule en ligne et en le renvoyant au planificateur. Par exemple, différents types de sol entraîneront des modifications dans les caractéristiques de glissement du véhicule, affectant ainsi l'état du véhicule. En combinant les paramètres estimés, la trajectoire peut être replanifiée en temps réel et la planification en boucle fermée peut améliorer la sécurité de la trajectoire.

3) Combinaison avec l'apprentissage automatique : Avec le développement rapide de l'intelligence artificielle représentée par les réseaux de neurones, de nombreux problèmes de planification traditionnels ont également apporté de nouvelles solutions. Dans le domaine de la conduite autonome, ses tendances de développement incluent :

• Modèle de bout en bout : utilisez un réseau neuronal profond pour dériver le signal de commande du véhicule directement en fonction de l'état du véhicule et des informations sur l'environnement externe. Bien que le modèle de bout en bout actuel ne soit pas interprétable comme une « boîte noire », on pense qu'à mesure que les humains continuent d'approfondir leur compréhension des réseaux neuronaux profonds, cette méthode présente un fort potentiel de développement en raison de ses avantages exceptionnels en matière de simplicité et d'efficacité.
• Intégration de modules de prise de décision et de planification de mouvement
• Les véhicules autonomes prennent des décisions optimales dans des environnements complexes. Par conséquent, comme mentionné ci-dessus, avec le développement rapide de la technologie d'apprentissage par renforcement profond, De plus en plus d'équipes de recherche ont commencé à l'appliquer à la planification décisionnelle de conduite autonome, en intégrant des modules de prise de décision comportementale et de planification de mouvement pour apprendre directement les trajectoires de conduite. Afin de résoudre le problème de la difficulté à obtenir la fonction de récompense environnementale, il a également été proposé d'utiliser d'abord l'apprentissage par renforcement inverse (IRL) pour apprendre sur la base de démonstrations d'experts humains, puis d'utiliser l'apprentissage par renforcement pour apprendre la politique optimale.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!