Une brève introduction à la boîte à outils Geatpy de l'algorithme génétique Python

Cet article vous apporte des connaissances pertinentes sur Python. Il présente principalement l'utilisation de la boîte à outils Geatpy de l'algorithme génétique Python. J'espère que cela sera utile.

【Recommandation associée : Tutoriel vidéo Python3】

1. Qu'est-ce qu'un algorithme génétique ?

L'algorithme génétique est un type d'algorithme de recherche construit artificiellement en simulant le mécanisme de la génétique biologique et de la sélection naturelle. Dans une certaine mesure, l'algorithme génétique est une simulation mathématique du processus d'évolution biologique. Le processus de survie des populations biologiques suit généralement les principes darwiniens de l'évolution. Les individus de la population sont sélectionnés ou éliminés par nature en fonction de leur capacité à s'adapter à l'environnement. Les résultats du processus évolutif se reflètent dans la structure de l'individu. Son chromosome contient plusieurs gènes. La connexion correspondante entre phénotype et génotype reflète la relation logique entre les caractéristiques externes et le mécanisme interne de l'individu. S'adapter à l'environnement naturel par croisement et mutation entre individus. Les chromosomes biologiques sont représentés mathématiquement ou informatiquement comme une suite de nombres, encore appelés chromosomes, parfois aussi appelés individus ; l'adaptabilité se mesure par une valeur numérique correspondant à un chromosome ; la sélection ou l'élimination des chromosomes se fait en fonction du problème rencontré. ou minimum.

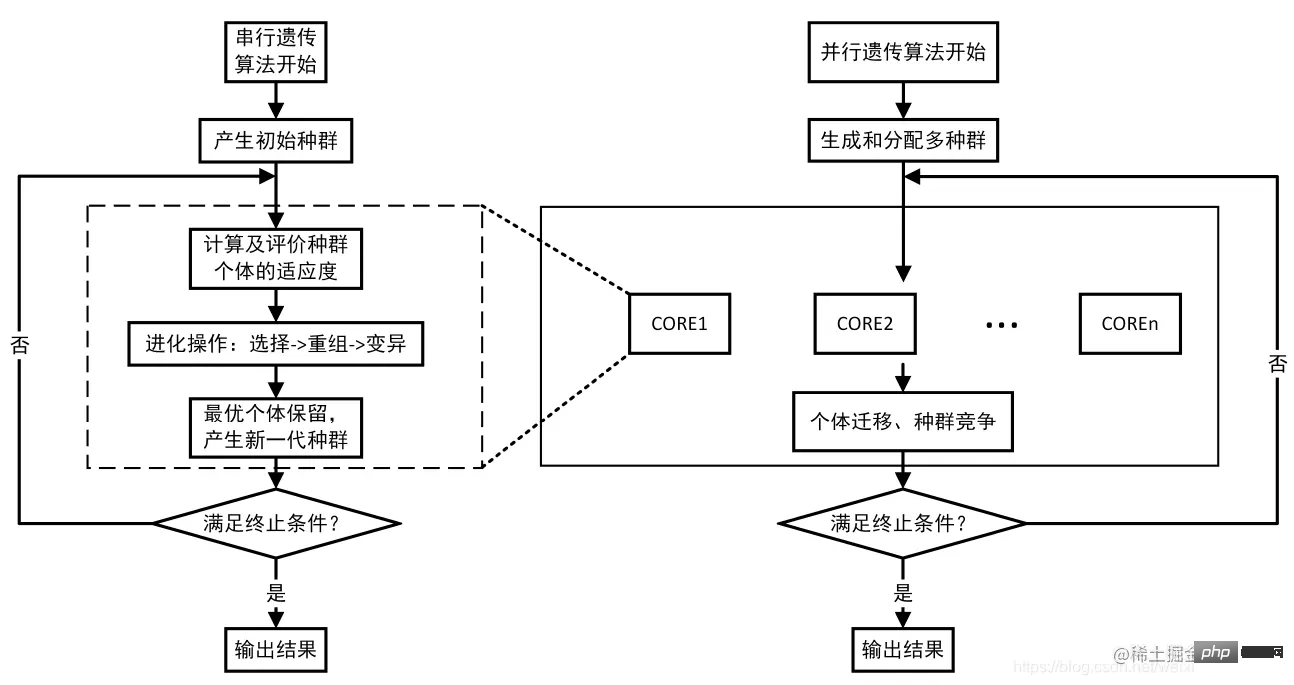
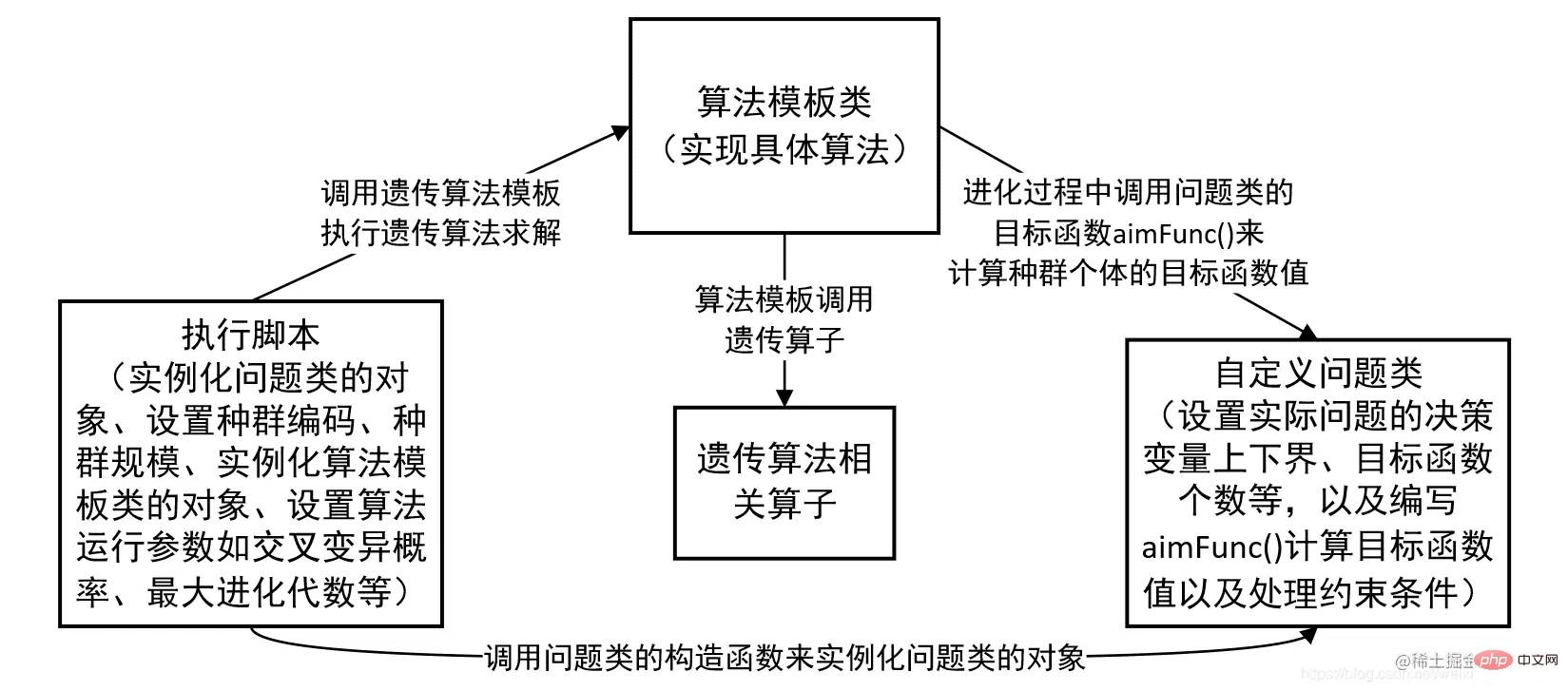
2. Bibliothèque d'algorithme génétique GEATPY

2.1 ALGORIHME GÉNÉTIQUE PARAMER GEATPY PARAMET PINDORMADE

API Document de référence officiel

Paramètre de la population [Attributs importants: Chrom, Phen, OBJV, CV, FITNV]

• sizes : int - taille de la population, c'est-à-dire le nombre d'individus dans la population.
• ChromNum : int - Le nombre de chromosomes, c'est-à-dire le nombre de chromosomes que possède chaque individu.
• Encodage : str - méthode d'encodage des chromosomes, 'BG' : encodage binaire/Gray ; 'RI' : encodage d'entiers réels, c'est-à-dire un encodage mixte de nombres réels et d'entiers ; - matrice de décodage
• Chrom : array - matrice de chromosomes de population, chaque ligne correspond à un chromosome d'un individu.
• Lind : int - longueur des chromosomes de la population.
• ObjV : tableau - matrice de valeur de fonction objectif de population, chaque ligne correspond à la valeur de fonction objectif d'un individu, chaque colonne correspond à un objectif
• FitnV : tableau - vecteur colonne de forme physique individuelle de population, chaque élément correspond à la forme physique d'un individuel, L'aptitude minimale est de 0
• CV : tableau - CV (Constraint Violation Value) est une matrice utilisée pour décrire quantitativement le degré de violation des conditions de contrainte. Chaque ligne correspond à un individu, et chaque colonne correspond à une contrainte
.
• Phen : array - Matrice de phénotype de population (C'est-à-dire une matrice composée des variables de décision représentées par chaque chromosome de la population après décodage).
• Si les contraintes sont définies en fonction de la règle de faisabilité via la matrice CV, alors les contraintes d'inégalité doivent être ≤ et les contraintes d'égalité doivent être transmises dans abs() (car cela suit le principe selon lequel plus la valeur est grande, plus plus petite la condition physique)

ea.Problem.

init
• () lbin et ubin (matrice de limite de plage variable de décision) représentent l'ouverture et la fermeture de l'intervalle de plage, 1 intervalle fermé et 0 intervalle ouvert

Introduction aux paramètres de résultat Geatpy

success : Vrai ou Faux, indiquant si l'algorithme a été résolu avec succès.

stopMsg : Une chaîne qui stocke la raison de l'arrêt de l'algorithme. success: True or False, 表示算法是否成功求解。

stopMsg: 存储着算法停止原因的字符串。

optPop: 存储着算法求解结果的种群对象。如果无可行解，则optPop.sizes=0。optPop.Phen为决策变量矩阵，optPop.ObjV为目标函数值矩阵。

lastPop: 算法进化结束后的最后一代种群对象。

Vars: 等于optPop.Phen，此处即最优解。若无可行解，则Vars=None。

ObjV: 等于optPop.ObjV，此处即最优解对应的目标函数值。若无可行解，ObjV=None。

CV: 等于optPop.CV，此处即最优解对应的违反约束程度矩阵。若无可行解，CV=None。

startTime: 程序执行开始时间。

endTime: 程序执行结束时间。

executeTime: 算法 所用时间。

nfev: 算法评价次数

gd: (多目标优化且给定了理论最优解时才有) GD指标值。

igd: (多目标优化且给定了理论最优解时才有) IGD指标值。

hv: (多目标优化才有) HV指标值。

spacing

optPop : Objet de population qui stocke les résultats de la solution algorithmique. S'il n'y a pas de solution réalisable, optPop.sizes=0. optPop.Phen est la matrice des variables de décision, optPop.ObjV est la matrice des valeurs de la fonction objectif. 🎜🎜lastPop : L'objet de population de dernière génération une fois l'évolution de l'algorithme terminée. 🎜🎜Vars : égal à optPop.Phen, voici la solution optimale. S'il n'y a pas de solution réalisable, Vars=None. 🎜🎜ObjV : égal à optPop.ObjV, qui est la valeur de la fonction objectif correspondant à la solution optimale. S'il n'y a pas de solution réalisable, ObjV=Aucune. 🎜🎜CV : égal à optPop.CV, voici la matrice des degrés de violation de contrainte correspondant à la solution optimale. S'il n'y a pas de solution réalisable, CV=Aucune. 🎜🎜startTime : heure de début d'exécution du programme. 🎜🎜endTime : L'heure de fin d'exécution du programme. 🎜🎜executeTime : Le temps pris par l'algorithme. 🎜🎜nfev : Nombre d'évaluations de l'algorithme 🎜🎜gd : (disponible uniquement pour l'optimisation multi-objectif et la solution optimale théorique est donnée) Valeur de l'indice GD. 🎜🎜igd : (disponible uniquement pour l'optimisation multi-objectifs et la solution optimale théorique est donnée) Valeur de l'indicateur IGD. 🎜🎜hv : (disponible uniquement pour l'optimisation multi-objectifs) Valeur de l'indicateur HV. 🎜🎜spacing : (disponible uniquement pour l'optimisation multi-objectifs) Valeur de l'indicateur d'espacement. 🎜

3. Meilleures pratiques

3.1 Exemple de code | Modèle de paramètres

Ensemble de solutions :

header_regex = '|'.join(['{}'] * len(headers))
header_str = header_regex.format(*[str(key).center(width) for key, width in zip(headers, widths)])
print("=" * len(header_str))
            print(header_str)
            print("-" * len(header_str))

gen : Algèbre évolutive
eval : Enregistrez le nombre d'évaluations
f_opt : individu optimal contemporain La valeur de fonction objectif de
f_max=valeur de fonction maximale de la population contemporaine
f_min minimum f_avg : niveau moyen
f_std : niveau de contrainte standard

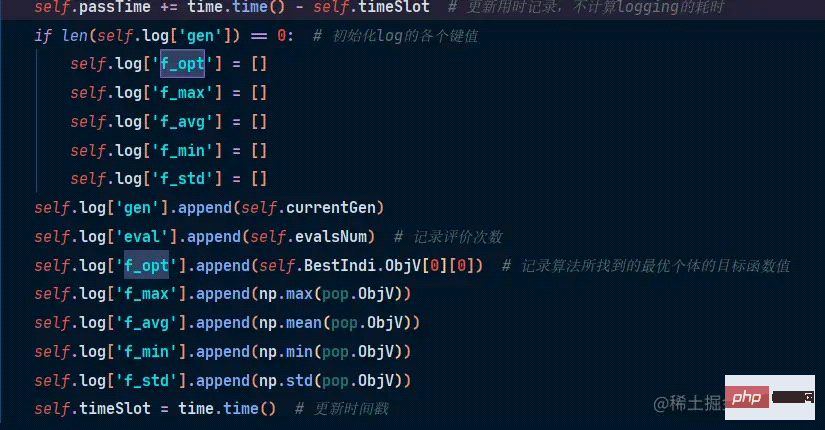
3.2 Meilleures pratiques

Utilisez la bibliothèque geatpy pour résoudre le plus court graphe acyclique dirigé Road

Code [Chemin le plus court] 1 : Utilisez la bibliothèque geatpy

import numpy as np
import geatpy as ea
class MyProblem(ea.Problem):  # 继承Problem父类
    def __init__(self):
        name = 'Shortest_Path'  # 初始化name（函数名称，可以随意设置）
        M = 1  # 初始化M（目标维数）
        maxormins = [1]  # 初始化maxormins（目标最小最大化标记列表，1：最小化该目标；-1：最大化该目标）
        Dim = 10  # 初始化Dim（决策变量维数）
        varTypes = [1] * Dim  # 初始化varTypes（决策变量的类型，元素为0表示对应的变量是连续的；1表示是离散的）
        lb = [0] * Dim  # 决策变量下界
        ub = [9] * Dim  # 决策变量上界
        lbin = [1] * Dim  # 决策变量下边界 1表示闭合区间，0表示开区间
        ubin = [1] * Dim  # 决策变量上边界
        # 调用父类构造方法完成实例化
        ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin)
        # 设置每一个结点下一步可达的结点（结点从1开始数，因此列表nodes的第0号元素设为空列表表示无意义）
        self.nodes = [[], [2, 3], [3, 4, 5], [5, 6], [7, 8], [4, 6], [7, 9], [8, 9], [9, 10], [10]]
        # 设置有向图中各条边的权重
        self.weights = {'(1, 2)': 36, '(1, 3)': 27, '(2, 4)': 18, '(2, 5)': 20, '(2, 3)': 13, '(3, 5)': 12,
                        '(3, 6)': 23,
                        '(4, 7)': 11, '(4, 8)': 32, '(5, 4)': 16, '(5, 6)': 30, '(6, 7)': 12, '(6, 9)': 38,
                        '(7, 8)': 20,
                        '(7, 9)': 32, '(8, 9)': 15, '(8, 10)': 24, '(9, 10)': 13}
    def decode(self, priority):  # 将优先级编码的染色体解码得到一条从节点1到节点10的可行路径
        edges = []  # 存储边
        path = [1]  # 结点1是路径起点
        while not path[-1] == 10:  # 开始从起点走到终点
            currentNode = path[-1]  # 得到当前所在的结点编号
            nextNodes = self.nodes[currentNode]  # 获取下一步可达的结点组成的列表
            chooseNode = nextNodes[np.argmax(
                priority[np.array(nextNodes) - 1])]  # 从NextNodes中选择优先级更高的结点作为下一步要访问的结点，因为结点从1数起，而下标从0数起，因此要减去1
            path.append(chooseNode)
            edges.append((currentNode, chooseNode))
        return path, edges
    def aimFunc(self, pop):  # 目标函数
        pop.ObjV = np.zeros((pop.sizes, 1))  # 初始化ObjV
        for i in range(pop.sizes):  # 遍历种群的每个个体，分别计算各个个体的目标函数值
            priority = pop.Phen[i, :]
            path, edges = self.decode(priority)  # 将优先级编码的染色体解码得到访问路径及经过的边
            pathLen = 0
            for edge in edges:
                key = str(edge)  # 根据路径得到键值，以便根据键值找到路径对应的长度
                if not key in self.weights:
                    raise RuntimeError("Error in aimFunc: The path is invalid. (当前路径是无效的。)", path)
                pathLen += self.weights[key]  # 将该段路径长度加入
            pop.ObjV[i] = pathLen  # 计算目标函数值，赋值给pop种群对象的ObjV属性
## 执行脚本
if __name__ == "__main__":
    # 实例化问题对象
    problem = MyProblem()
    # 构建算法
    algorithm = ea.soea_EGA_templet(problem,
                                    ea.Population(Encoding='RI', NIND=4),
                                    MAXGEN=10,  # 最大进化代数
                                    logTras=1)  # 表示每隔多少代记录一次日志信息
    # 求解
    res = ea.optimize(algorithm, verbose=True, drawing=1, outputMsg=False, drawLog=False, saveFlag=True,
                      dirName='result')
    print('最短路程为：%s' % (res['ObjV'][0][0]))
    print('最佳路线为：')
    best_journey, edges = problem.decode(res['Vars'][0])
    for i in range(len(best_journey)):
        print(int(best_journey[i]), end=' ')
    print()

[Recommandations associées : Tutoriel vidéo Python3 ]

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!