Maison >base de données >tutoriel mysql >Parlons de la couche inférieure et de l'optimisation de l'index Mysql
Parlons de la couche inférieure et de l'optimisation de l'index Mysql
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBavant
- 2022-02-14 18:47:541965parcourir
Cet article vous apporte des connaissances pertinentes sur l'index sous-jacent et l'optimisation dans mysql. Trions les points de connaissances sur l'indexation dans MySQL. J'espère qu'il sera utile à tout le monde.

Indice Mysql
Récemment, j'ai lu des articles sur l'indexation sur de nombreux sites Web, mais ils ne sont pas exhaustifs. Certains concepts sont très vagues. Ce qui suit est l'index Mysql compilé par l'éditeur Knowledge Points. .
1. Tout d'abord, parlons de ce qu'est un index et pourquoi nous devons utiliser un index.
L'index est utilisé pour trouver rapidement des lignes avec une valeur spécifique dans une colonne, sans utiliser d'index, MySQL doit lire l'intégralité de l'enregistrement. en commençant par le premier enregistrement de la table jusqu'à ce que les lignes pertinentes soient trouvées. Plus la table est grande, plus il faut de temps pour interroger les données. Si la colonne de la table est indexée, MySQL peut rapidement accéder à un endroit pour rechercher le fichier de données. sans avoir à regarder toutes les données, cela vous fera gagner beaucoup de temps.
2. Les types d'index sont divisés en deux catégories :
1.hash index
2.bTree
3 Analysons brièvement l'index de hachage et l'index bTree.
1. Une table de hachage est une structure qui stocke les données dans un format clé-valeur Tant que nous saisissons la clé à trouver, qui est clé, nous pouvons trouver sa valeur correspondante, qui est Valeur. L'idée du hachage est très simple. Mettez la valeur dans le tableau, utilisez une fonction de hachage pour convertir la clé à une certaine position, puis placez la valeur à cette position dans le tableau.
Inévitablement, plusieurs valeurs clés auront la même valeur après avoir été converties par la fonction de hachage. Une façon de gérer cette situation consiste à créer une liste chaînée.
2. En parlant de bTree, nous devons mentionner les arbres binaires. Les arbres binaires sont divisés en plusieurs types, tels que : Arbre de recherche binaire, arbre binaire équilibré, etc. Bien sûr, il y a aussi le point culminant les arbres rouges et noirs.
1) Les caractéristiques d'un arbre de recherche binaire sont : Les valeurs de tous les nœuds du sous-arbre gauche du nœud parent sont inférieures à la valeur du nœud parent. Les valeurs de tous les nœuds du sous-arbre de droite sont supérieures à la valeur du nœud parent. Prenons une photo comme exemple pour illustrer l'arbre de recherche binaire.
| ID | nom |
|---|---|
| 5 | Zhang Wu |
| 6 | Zhang Liu |
| 7 | Zhang |
| 2 | 张二 |
| 1 | Zhang Yi |
| 4 | Zhang Si |
| 3 | Zhang San |
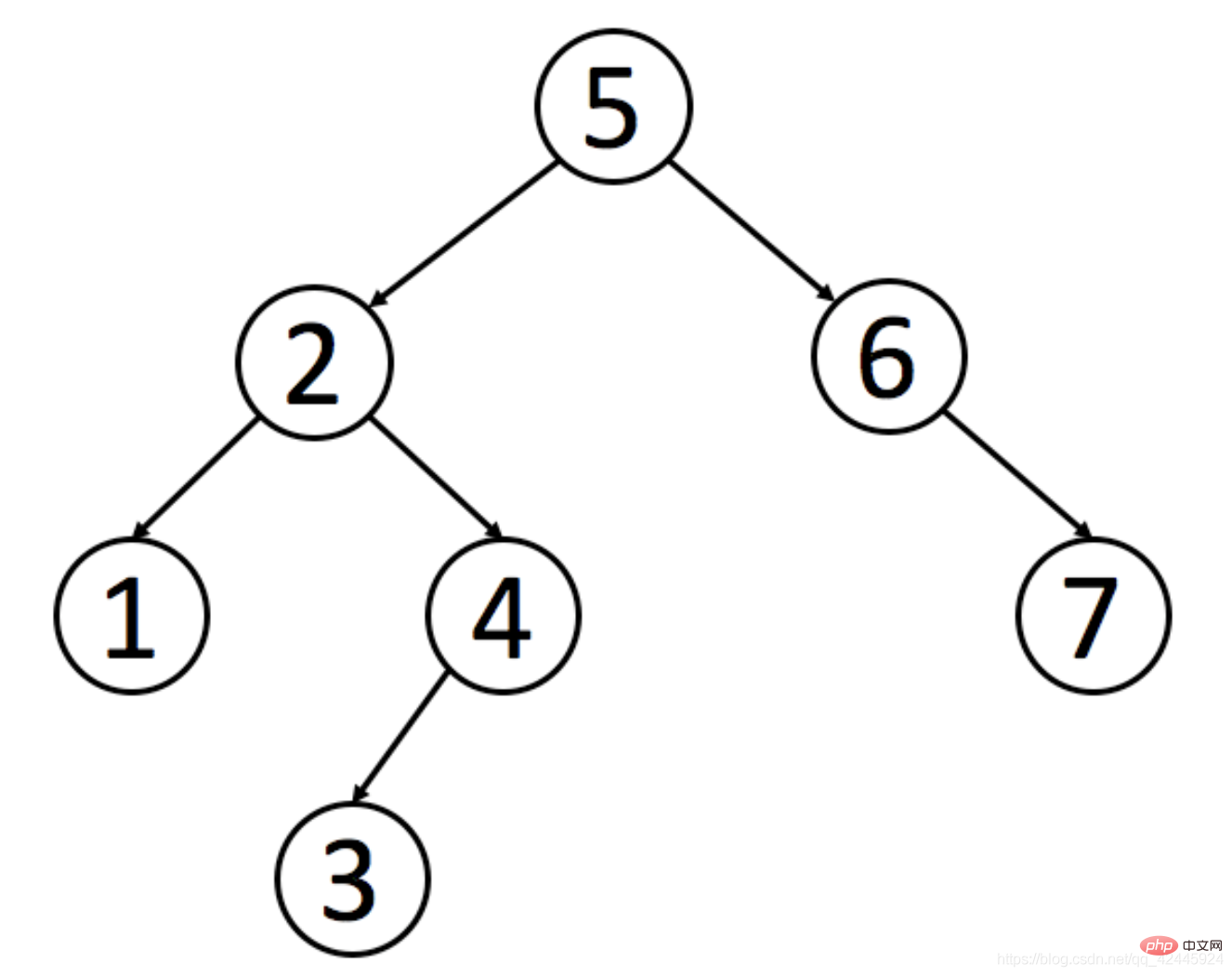 Il est nécessaire de trouver Zhang San. Si nous n'utilisons pas l'arbre de recherche binaire, nous devons chercher 7 fois. En utilisant l'arbre de recherche binaire, nous n'avons besoin de chercher que 4 fois pour trouver la valeur souhaitée.
Il est nécessaire de trouver Zhang San. Si nous n'utilisons pas l'arbre de recherche binaire, nous devons chercher 7 fois. En utilisant l'arbre de recherche binaire, nous n'avons besoin de chercher que 4 fois pour trouver la valeur souhaitée.
D'après ce qui précède, l'utilisation d'un arbre de recherche binaire peut en effet réduire le nombre de requêtes, mais avez-vous déjà pensé à ce qui se passerait si les données de la base de données augmentaient dans une séquence telle que 1, 2, 3, 4, 5, 6 et 7 ? Continuer à utiliser L'arbre de recherche binaire deviendra une liste chaînée. Donc, si nous voulons trouver 7, nous devons chercher 7 fois et parcourir le tableau 7 fois. Ce n'est pas différent de ne pas créer d'index, ce qui est aussi l'un des inconvénients. La figure suivante est un exemple. 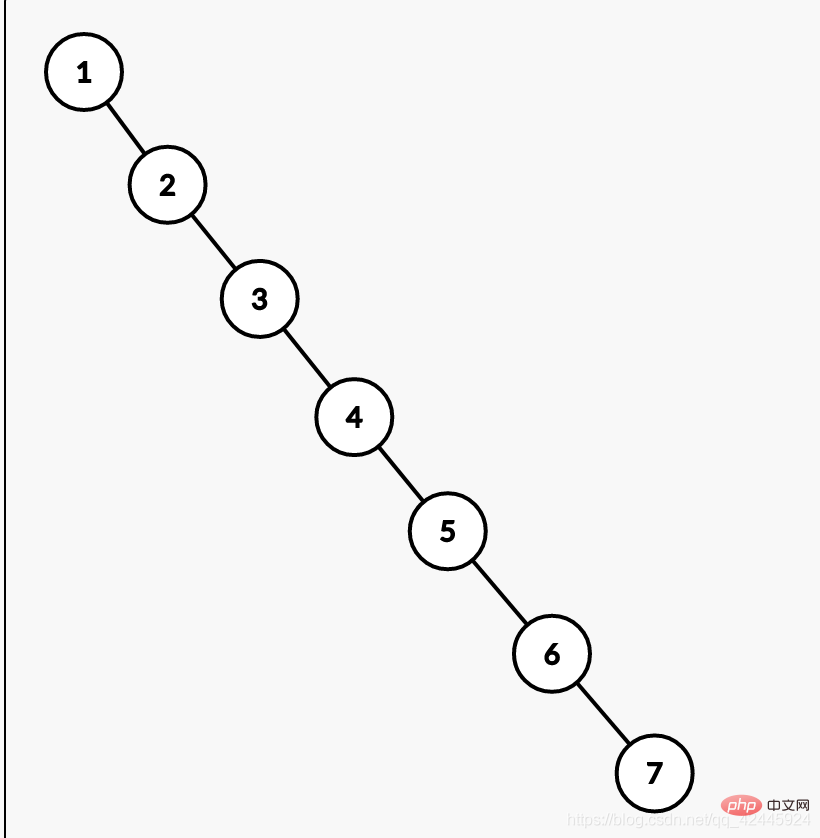
2) Arbre binaire équilibré : également connu sous le nom d'arbre AVL, la valeur absolue de la différence de hauteur entre ses sous-arbres gauche et droit ne dépasse pas 1, et les sous-arbres gauche et droit sont tous deux des arbres binaires équilibrés. L'arbre AVL est le premier arbre de recherche binaire auto-équilibré inventé. Dans un arbre AVL, la différence de hauteur maximale entre deux sous-arbres de n'importe quel nœud ne peut être que de 1, c'est pourquoi on l'appelle également arbre équilibré en hauteur. L'interrogation, l'ajout et la suppression sont O (log n) dans le cas moyen et dans le pire des cas. Les ajouts et suppressions peuvent nécessiter une ou plusieurs rotations d’arbre pour rééquilibrer l’arbre.
Le but de l'introduction des arbres binaires est d'améliorer l'efficacité de la recherche d'arbre binaire et ainsi de réduire la longueur moyenne de recherche de l'arbre. À cette fin, nous devons ajuster la structure de l'arbre lors de l'insertion d'un nœud dans chaque arbre binaire afin que le. La recherche d'arbre binaire peut maintenir l'équilibre. Il est possible de réduire la hauteur de l'arbre, réduisant ainsi la longueur moyenne de recherche d'arbre.
Les caractéristiques d'un arbre binaire équilibré sont les suivantes :
1. Son sous-arbre gauche et son sous-arbre droit sont tous deux des arbres AVL
2. La différence de hauteur entre le sous-arbre gauche et le sous-arbre droit ne peut pas dépasser 1
Exemple : 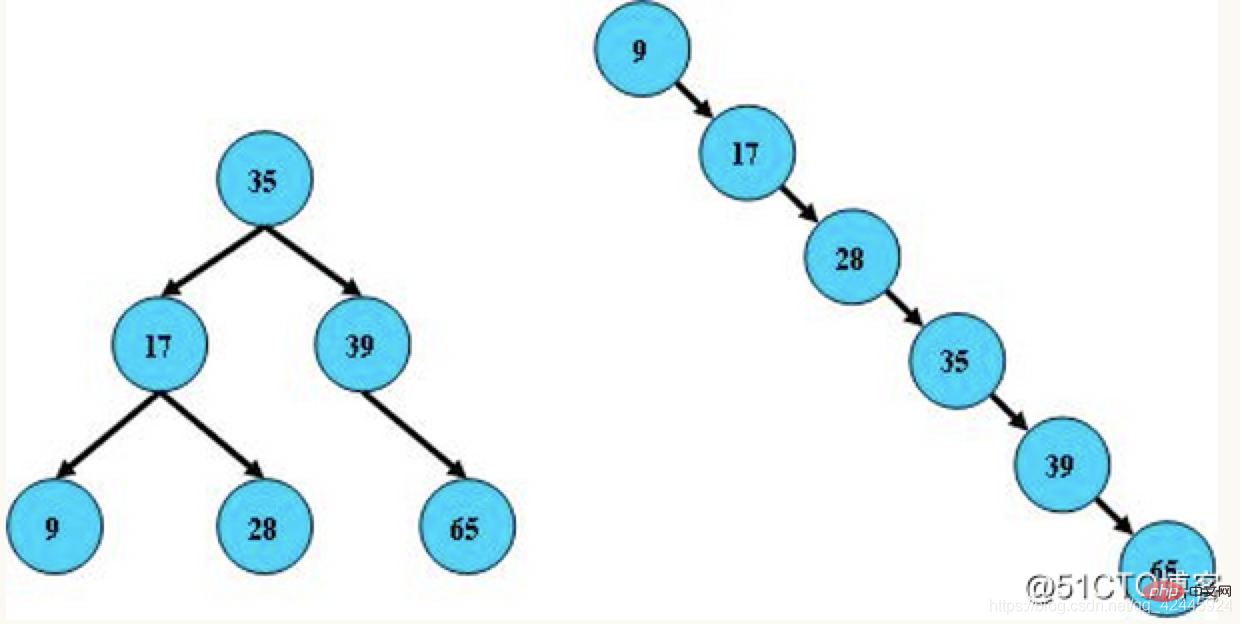 3) Arbre rouge-noir : On peut comprendre que l'arbre rouge-noir est un arbre supérieur à l'arbre binaire équilibré. L'arbre rouge-noir ne recherche pas « l'équilibre complet ». répondre aux exigences d'équilibre, réduisant les exigences de rotation, améliorant ainsi les performances. De plus, grâce à sa conception, tout déséquilibre peut être résolu en trois tours. Dans les arbres rouge-noir, la complexité temporelle de son algorithme est la même que celle d'AVL, et les performances statistiques forceront les arbres AVL à être plus élevés. Par conséquent, comparé à l'arbre binaire équilibré, l'arbre rouge-noir n'est pas un arbre binaire équilibré au sens strict. L'efficacité d'insertion et de suppression de l'arbre rouge-noir est plus élevée et l'efficacité des requêtes est relativement inférieure à celle de l'arbre binaire équilibré. Tree Cependant, la différence d'efficacité des requêtes entre les deux est fondamentalement négligeable. Les caractéristiques des arbres rouge-noir sont les suivantes :
3) Arbre rouge-noir : On peut comprendre que l'arbre rouge-noir est un arbre supérieur à l'arbre binaire équilibré. L'arbre rouge-noir ne recherche pas « l'équilibre complet ». répondre aux exigences d'équilibre, réduisant les exigences de rotation, améliorant ainsi les performances. De plus, grâce à sa conception, tout déséquilibre peut être résolu en trois tours. Dans les arbres rouge-noir, la complexité temporelle de son algorithme est la même que celle d'AVL, et les performances statistiques forceront les arbres AVL à être plus élevés. Par conséquent, comparé à l'arbre binaire équilibré, l'arbre rouge-noir n'est pas un arbre binaire équilibré au sens strict. L'efficacité d'insertion et de suppression de l'arbre rouge-noir est plus élevée et l'efficacité des requêtes est relativement inférieure à celle de l'arbre binaire équilibré. Tree Cependant, la différence d'efficacité des requêtes entre les deux est fondamentalement négligeable. Les caractéristiques des arbres rouge-noir sont les suivantes :
1. Les nœuds sont rouges ou noirs.
2. Le nœud racine est noir.
3. Les deux nœuds enfants de chaque nœud rouge sont noirs. (Les enfants des nœuds rouges doivent être des nœuds noirs)
4. Tous les chemins d'un nœud à chacune de ses feuilles contiennent le même nombre de nœuds noirs.
Par conséquent, l'arbre rouge-noir est un arbre équilibré en noir, et la différence de hauteur entre le sous-arbre gauche et le sous-arbre droit ne dépassera pas 2. Le nœud parent et le nœud enfant d'un nœud rouge ne peuvent être qu'un nœud noir.
Exemple : 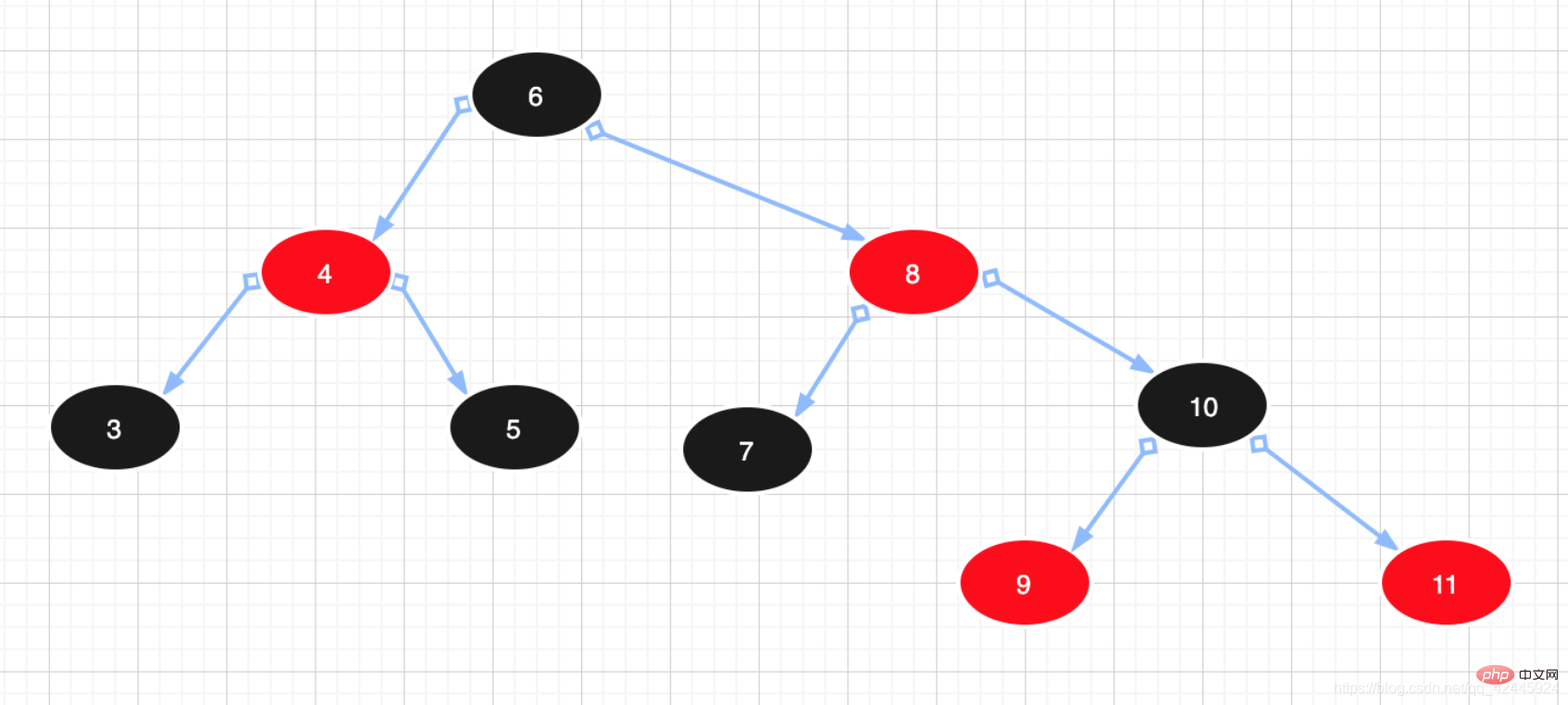
4) BTree (B-tree) : Bien sûr, l'arbre rouge-noir mentionné ci-dessus, la performance est très élevée. En prenant la figure ci-dessus comme exemple, la hauteur maximale de l'arborescence est de 4, avec un total de 9 données. Cependant, pour la base de données Mysql, s'il y a des millions de données ou des dizaines de millions de données, alors la hauteur de l'arborescence sera incommensurable, par exemple, des centaines de données peuvent nécessiter 30 à 50 fois d'E/S disque pour interroger les données, voire plus, ce qui ne peut évidemment pas répondre à l'efficacité des requêtes. Index MySQL. Ainsi, si nous contrôlons la hauteur de l'arborescence, cela réduira considérablement le nombre de requêtes d'E/S disque. Si la hauteur est contrôlée à 4, alors seulement 4 E/S disque sont nécessaires pour interroger les données.
Mais comment contrôler la hauteur de l'arbre ? Les arbres rouge-noir ne stockent qu'un seul élément par nœud. Et si chaque nœud stocke plusieurs éléments ? Cela peut résoudre le problème de hauteur. Il doit y avoir des étudiants qui ont des questions Si. nous les mettons tous sur un seul nœud, la valeur de la hauteur sera 1. N'est-ce pas plus rapide ? C'est définitivement une erreur de penser de cette façon. Mysql a une limite de taille à chaque fois qu'il interagit avec le disque IO. Mysql limite la taille de chaque nœud à 16 Ko. Les étudiants qui souhaitent vérifier la limite de taille des nœuds de leur Mysql peuvent exécuter le SQL suivant.
afficher le statut global comme 'Innodb_page_size'
L'image suivante est utilisée comme exemple pour refléter les caractéristiques de BTree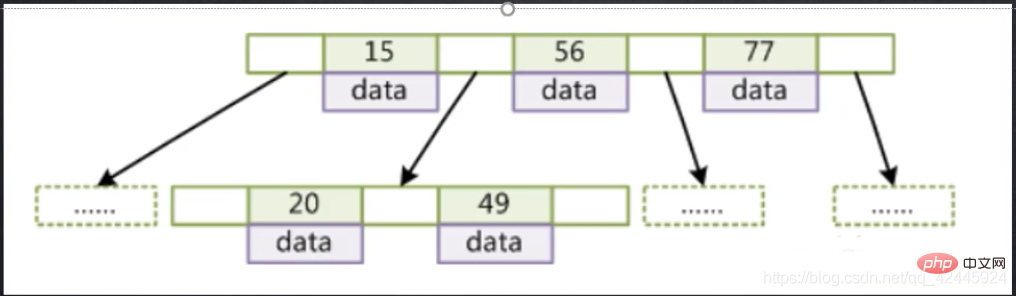 BTree comme suit :
BTree comme suit :
1. Tous les éléments d'index ne sont pas répétés
2. L'index de données du nœud augmente de de gauche à droite
3. Le nœud feuille a À la même profondeur, les pointeurs des nœuds feuilles sont vides
4. Les nœuds feuilles et les nœuds non feuilles stockent des index et des données
5) B+ tree : Comme mentionné ci-dessus, BTree contrôle la hauteur de l'arborescence, ce qui peut répondre aux besoins d'indexation de Mysql. Cependant, en fin de compte, l'implémentation de l'index Mysq n'est pas BTree mais B+ tree. un peu sur l'arbre B. Après transformation, l'arbre B+ a été obtenu, ce qui peut également être compris comme l'arbre B+ est une version améliorée de l'arbre B.
Prenons l'image comme exemple : 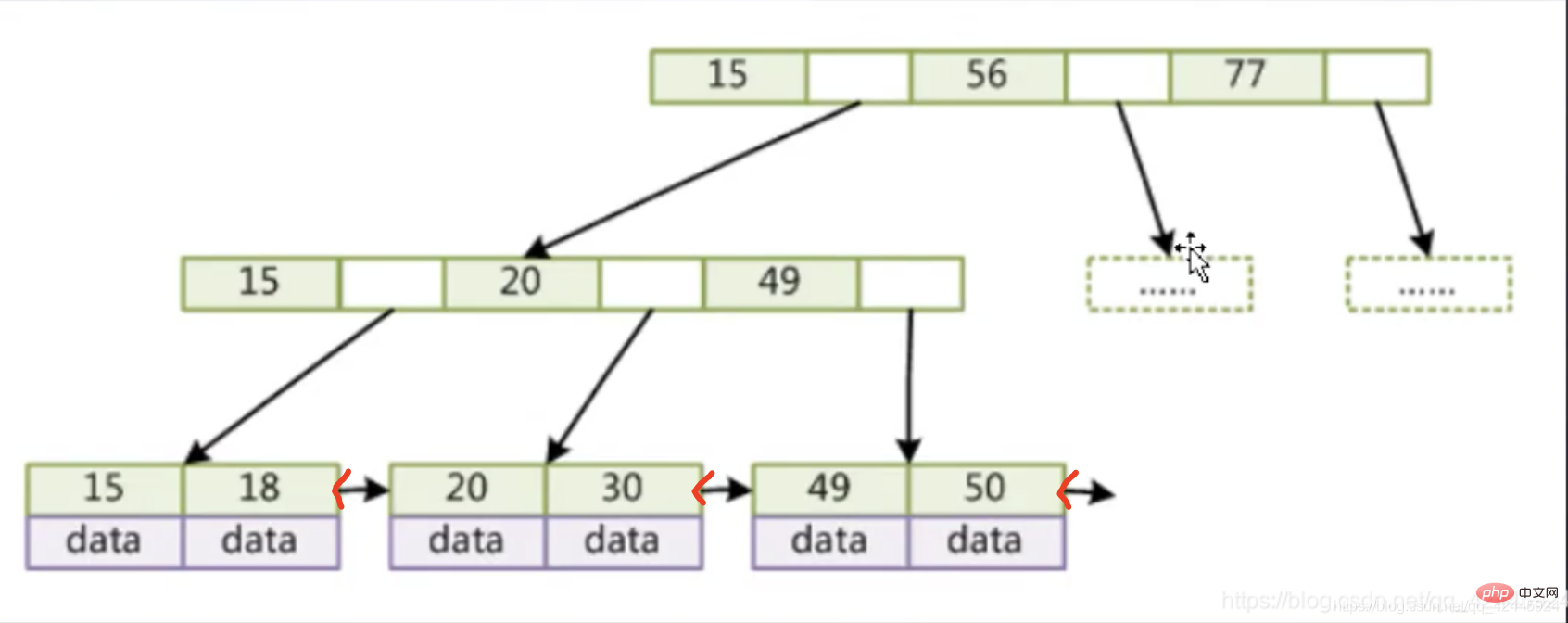
Comme vous pouvez le voir sur cette image, nos nœuds non-feuilles ne stockent que des index et non des données, et les nœuds feuilles sont connectés avec des pointeurs. Les nœuds feuilles et les nœuds non-feuilles de l'arbre B stockent des index et des données, et les pointeurs des nœuds feuilles sont vides. L'arbre B+ place les données sur les nœuds feuilles, afin que les nœuds non-feuilles puissent stocker plus d'index. , à chaque fois Plus d'index peuvent également être obtenus à partir du disque IO.
Les fonctionnalités de l'arbre B+ sont les suivantes :
1. Les nœuds non-feuilles ne stockent pas de données, seuls les index (redondants) et les pointeurs de niveau inférieur peuvent être placés
2. Les nœuds feuilles contiennent tous les champs d'index et les données.
3 .Les nœuds feuilles sont connectés avec des pointeurs doubles pour améliorer les performances de l'accès par intervalles
L'arbre B+ dessiné sur Baidu et de nombreux blogs est faux, assurez-vous d'éviter les pièges.
Si vous souhaitez voir l'explication officielle de Mysql sur les arbres B+, vous pouvez la consulter.
Lien : Site officiel de Mysql.
Quatre. Classification d'index
1. Classification selon l'association de stockage de l'index : Divisé en deux grandes catégories
1.) Index de cluster (index clusterisé) : Le nœud feuille contient les enregistrements de données complets qui n'ont pas besoin d'être renvoyés dans la table.
2.) Index non clusterisé : nécessité de renvoyer la table et de rechercher deux fois dans l'arborescence, ce qui affecte les performances.
1.1) Tout le monde sait qu'il existe deux moteurs de stockage couramment utilisés pour MySQL, MyISAM et InnoDB, mais avez-vous réellement compris les structures de stockage de données sous-jacentes des deux moteurs de stockage ?
Prenons l'image comme exemple pour expliquer : 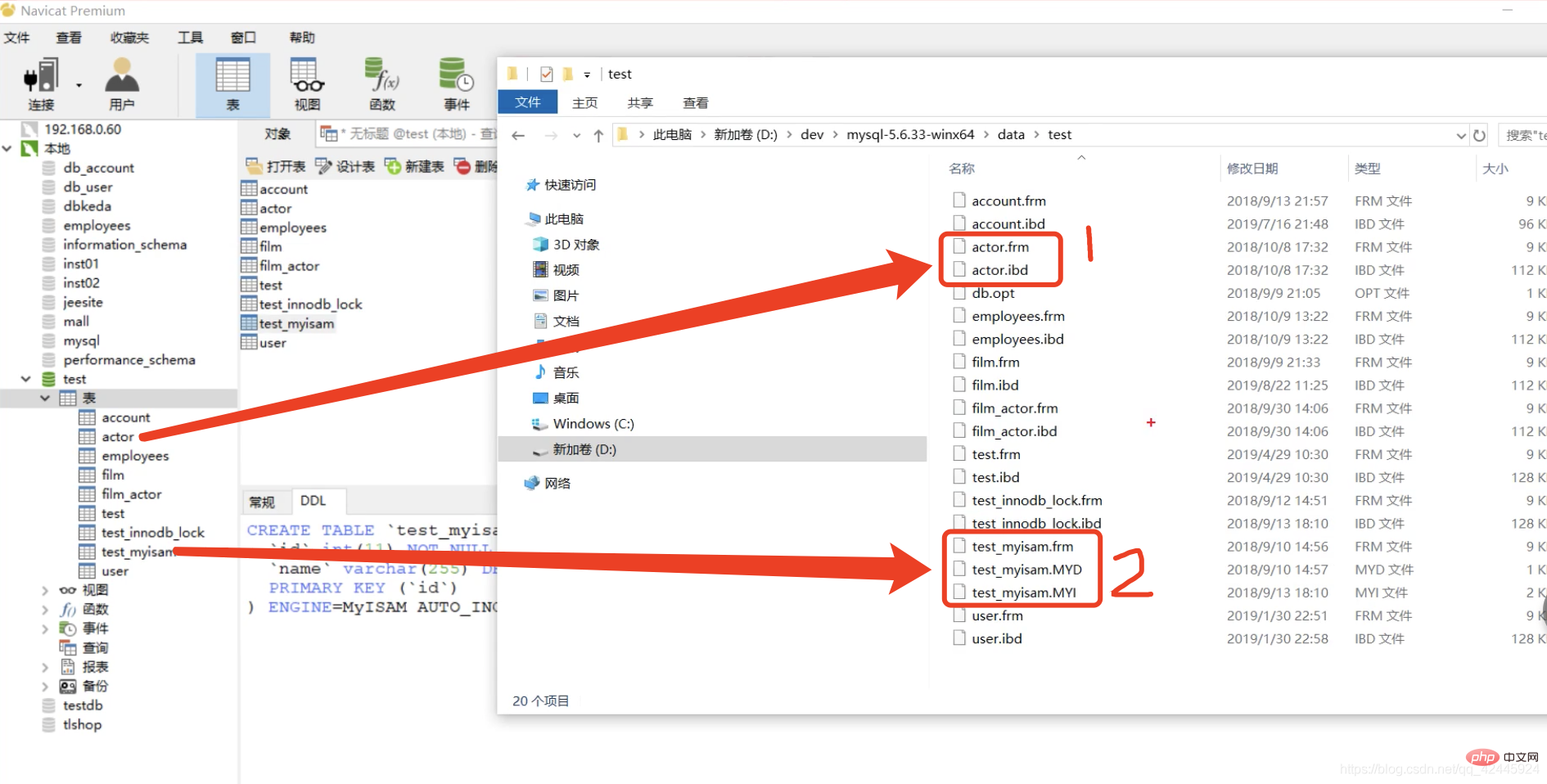 La table test.myisam est le moteur de stockage MyISAM, et la table acteur est le moteur de stockage InnoDB. Vous pouvez voir que le moteur de stockage MyISAM a trois fichiers, à savoir frm, MYD. , et MYI C'est facile à comprendre. L'abréviation de frm-frame stocke la structure de la table, MYD-MYData stocke les données et MYI-MYIndex stocke les index et les données sont stockés séparément. est également stocké. La structure de la table, les fichiers IBD stockent les index et les données, ce qui est différent d'InnoDB et MyISAM.
La table test.myisam est le moteur de stockage MyISAM, et la table acteur est le moteur de stockage InnoDB. Vous pouvez voir que le moteur de stockage MyISAM a trois fichiers, à savoir frm, MYD. , et MYI C'est facile à comprendre. L'abréviation de frm-frame stocke la structure de la table, MYD-MYData stocke les données et MYI-MYIndex stocke les index et les données sont stockés séparément. est également stocké. La structure de la table, les fichiers IBD stockent les index et les données, ce qui est différent d'InnoDB et MyISAM.
L'image suivante est utilisée comme exemple pour illustrer que l'index de clé primaire du moteur de stockage MyISAM nécessite une opération de retour de table (index non clusterisé)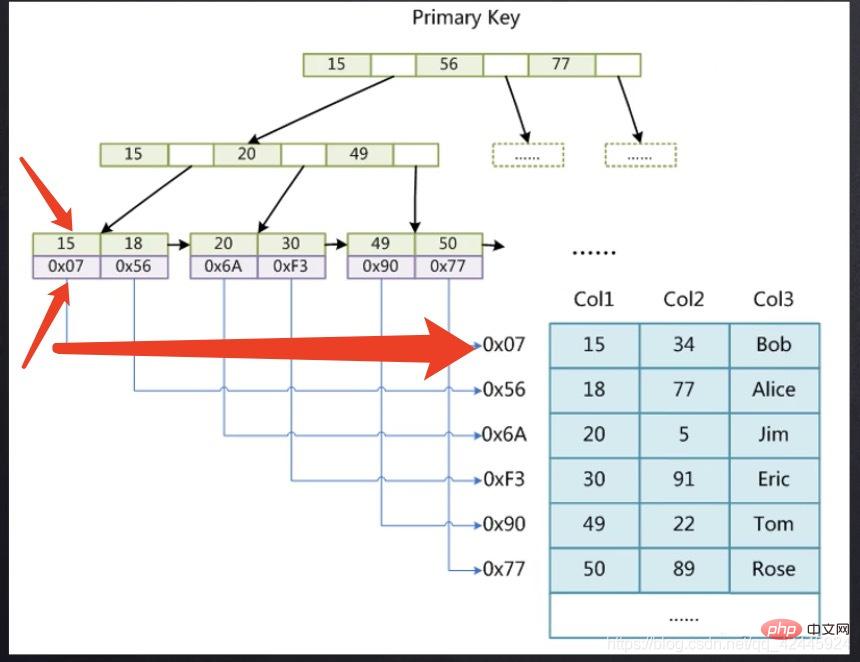 où 15 stocke l'index de clé primaire et 0x07 stocke le fichier disque pointeur d'adresse enregistré dans la ligne de 15, comme le nôtre. Si vous souhaitez trouver les données de 15, vous devez d'abord trouver le pointeur correspondant à 15 via l'arborescence d'index de clé primaire, puis trouver le pointeur puis accéder au fichier MyD. pour trouver les données spécifiques. Une deuxième recherche est nécessaire. Ce processus est appelé opération de retour de table.
où 15 stocke l'index de clé primaire et 0x07 stocke le fichier disque pointeur d'adresse enregistré dans la ligne de 15, comme le nôtre. Si vous souhaitez trouver les données de 15, vous devez d'abord trouver le pointeur correspondant à 15 via l'arborescence d'index de clé primaire, puis trouver le pointeur puis accéder au fichier MyD. pour trouver les données spécifiques. Une deuxième recherche est nécessaire. Ce processus est appelé opération de retour de table.
2.1) La figure suivante est utilisée comme exemple pour illustrer que l'index de clé primaire du moteur de stockage InnoDB ne nécessite pas d'opérations de retour de table. (Index clusterisé)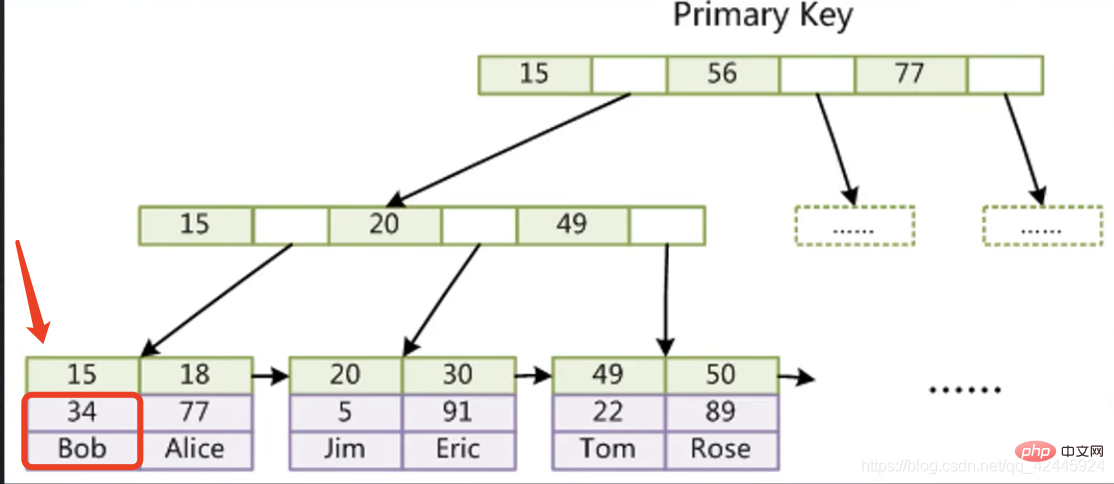 Le sous-nœud du moteur de stockage InnoDB stocke d'abord l'index dans la ligne 15, et la colonne en dessous de 15 stocke tous les autres champs de la ligne où se trouve l'index si nous voulons vérifier les données. sur 15, on peut le faire directement Trouvé sans avoir à passer par une seconde recherche arborescente.
Le sous-nœud du moteur de stockage InnoDB stocke d'abord l'index dans la ligne 15, et la colonne en dessous de 15 stocke tous les autres champs de la ligne où se trouve l'index si nous voulons vérifier les données. sur 15, on peut le faire directement Trouvé sans avoir à passer par une seconde recherche arborescente.
2. Classé par fonction : principalement divisé en cinq catégories
2.1 Index de clé primaire : l'index de clé primaire InnoDB ne nécessite pas d'opération de retour de table
2.2 Index ordinaire (index secondaire) : l'index ordinaire InnoDB nécessite un retour de table opération, Pour les index secondaires, ils seront indexés conjointement avec la clé primaire par défaut.
2.3 Index unique
2.4 Index de texte intégral
2.5 Index conjoint : nécessité de respecter le principe du préfixe le plus à gauche
3. Il a été mentionné en 2.2 que les index ordinaires nécessitent des opérations de retour de table, n'y a-t-il pas Besoin de renvoyer des tables ? Quant aux index ordinaires, la réponse est oui. Dans une certaine requête, l'index a couvert nos exigences de requête. Nous l'appelons un index de couverture. Pour le moment, il n’est pas nécessaire de revenir à la table.
Étant donné que l'index de couverture peut réduire le nombre de recherches dans l'arborescence et améliorer considérablement les performances des requêtes, l'utilisation de l'index de couverture est un moyen d'optimisation de performance courant.
Par exemple : ce qui suit est l'instruction d'initialisation de cette table.
mysql> create table T ( ID int primary key, k int NOT NULL DEFAULT 0, s varchar(16) NOT NULL DEFAULT '', index k(k)) engine=InnoDB; insert into T values(100,1, 'aa'),(200,2,'bb'), (300,3,'cc'),(500,5,'ee'),(600,6,'ff'),(700,7,'gg');
Dans le tableau T ci-dessus, si j'exécute select * from T où k entre 3 et 5, combien d'opérations de recherche dans l'arborescence doivent être effectuées et combien de lignes seront analysées ?
Jetons maintenant un coup d'œil au flux d'exécution de cette instruction de requête SQL. Regardez l'image ci-dessous. 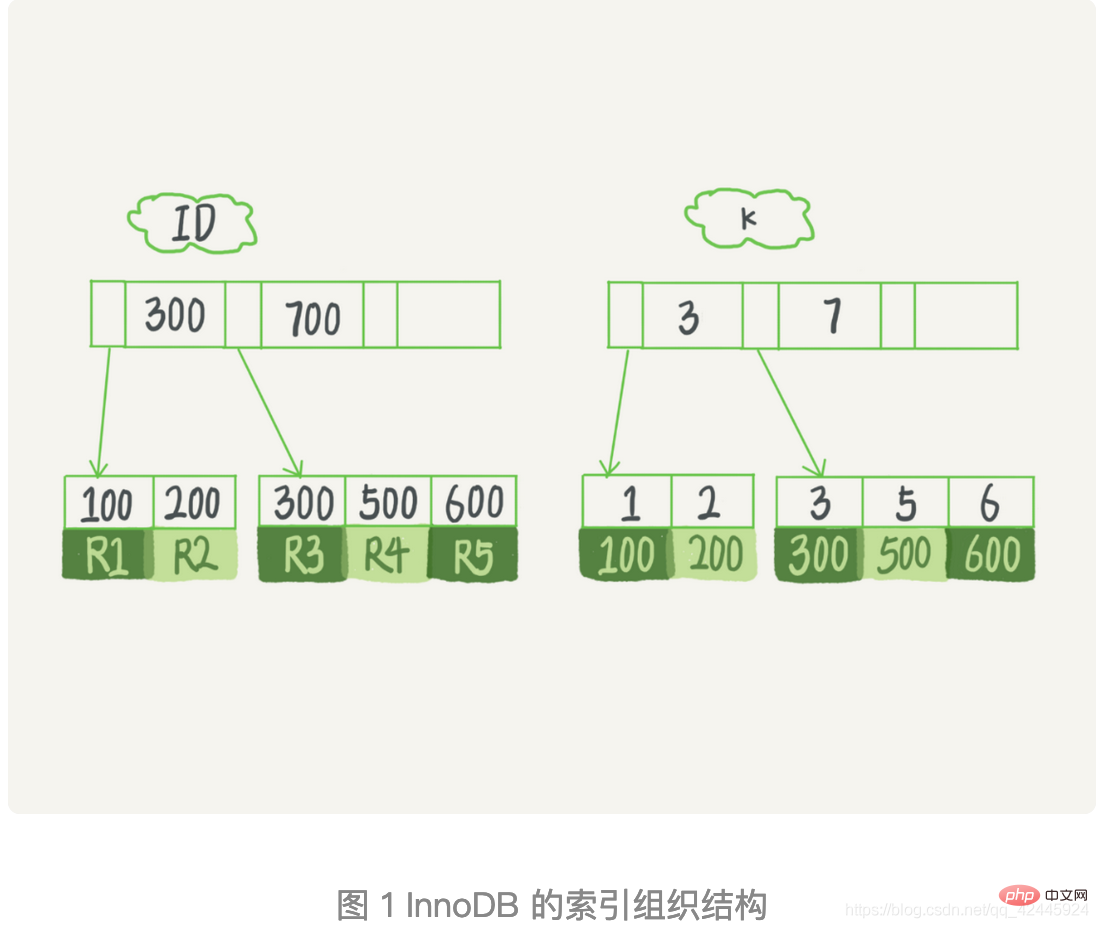
1.) Trouvez l'enregistrement k=3 dans l'arbre d'index k et obtenez ID = 300;
2.) Allez ensuite dans l'arbre d'index ID et trouvez le R3 correspondant à ID=300;
3.) Obtenez la valeur suivante k=5 dans l'arbre d'index k et obtenez ID=500 ;
4.) Revenez à l'arbre d'index ID et trouvez le R4 correspondant à ID=500 ;
Récupérez-le dans l'arbre d'index k La valeur suivante k=6 ne remplit pas la condition et la boucle se termine. Dans ce processus,
. On peut voir que ce processus de requête lit 3 enregistrements de l'arbre d'index k (étapes 1, 3 et 5) et renvoie la table deux fois (étapes 2 et 4). Dans cet exemple, puisque les données requises pour les résultats de la requête se trouvent uniquement sur l'index de clé primaire, elles doivent être renvoyées dans la table.
Si l'instruction exécutée est select ID from T où k entre 3 et 5,
À ce stade, il vous suffit de vérifier la valeur de ID, et la valeur de ID est déjà dans l'arborescence d'index k, donc les résultats de la requête peut être fourni directement sans retourner la table. C'est-à-dire que dans cette requête, l'index k a "couvert" nos exigences de requête, que nous appelons un index de couverture. Dans InnoDB, les tables sont stockées sous forme d'index basés sur l'ordre des clés primaires. Les tables stockées de cette manière sont appelées tables organisées en index. Et comme nous l'avons mentionné plus tôt, InnoDB utilise le modèle d'index d'arbre B+, donc les données sont stockées dans l'arborescence B+. Chaque index correspond à un arbre B+ dans InnoDB.
5. Optimisation des index
1. Ce qui précède décrit les concepts de base, les classifications et les connaissances de base liées à la structure des index. Parlons des connaissances pertinentes en matière d’optimisation d’index.
1.) Lorsqu'une seule colonne de l'index combiné contient une valeur nulle, l'index devient invalide2.)
L'index calculé sur la colonne devient invalide et tous les index après la plage sont invalides3 .)
Sur les conditions de requête, l'utilisation de fonctions entraînera un échec de l'index4.)
Utilisez les opérateurs != ou dans les clauses Where, provoquant un échec de l'index5.)
Évitez d'utiliser or, ce qui entraînera un échec de l'index. 6.)
L'utilisation de requêtes floues entraînera également un échec de l'index. Vous pouvez utiliser like 'a%' au lieu de like '%a%'7.)
Essayez d'utiliser des index de couverture et réduisez les instructions select *8. .)
Satisfaites à la règle du préfixe le plus à gauche. Commencez par la colonne la plus à gauche et ne sautez pas de colonnes dans l'index 9.)
L'index échouera si la chaîne n'est pas placée entre guillemets simples 2. explication de l’optimisation des index.
Créez une nouvelle table d'employés avec 5 attributs, comme suit.
create table employees(
id int primary key auto_increment comment '主键自增',
name varchar(30) not null default '' comment'名字',
age int not null default 1 comment '年龄',
id_card varchar(40) not null default '' comment '身份证号',
position varchar(40) not null default '' comment '位置'
);
-- 创建联合索引
create index name_index on employees (name,age,position);
-- 插入一条数据
insert into employees(name,age,id_card,position) values('张三',15,
'201124199011035321','北京');
-- 下面以10条sql测试,注意建立的联合索引顺序是 name,age,position 1.explain select * from employees where age=15 and position='北京' and name='张三'; 2.explain select * from employees where name='张三' and age=15 and position='北京'; 3.explain select * from employees where age=15 and name='张三'; 4.explain select * from employees where position='北京' and name='张三'; 5.explain select * from employees where position='北京' and age=15; 6.explain select * from employees where position='北京' and age>15 and name='张三'; 7.explain select * from employees where position='北京'; 8.explain select * from employees where age=15; 9.explain select * from employees where name='张三'; 10.explain select * from employees where name != '张三';
以上10条sql有哪些是索引失效,有哪些是索引没有失效的呢? 相信同学们已经有了答案,但是答案对不对呢,下面我们一起分析下。 首先说第1条,查询条件把3个索引全部用上了,但是索引的顺序有变化,由name,age,position变成 了age,position,name,想到这里肯定有很多同学给出的答案就是索引失效,但是事实证明这个结果 是错的,索引生效,肯定有很多同学疑惑,为什么呢,这条sql不满足最左原则法则呀,这就要涉及到sql 的执行流程了,这里博主简单说下,sql执行有1个优化器的过程,优化器的作用之一就是索引的选择优化, 所以优化器帮我们把索引的顺序变成正确的了,所以索引生效。 下面是第1条按照索引顺序sql和第2条没有按照索引顺序sql的执行结果。 执行结果入下图:可以发现全部生效。
La valeur du premier type SQL est ref, l'octet est 288 et ref a 3 const, qui sont tous valides.
La valeur du deuxième type SQL est ref, l'octet est 288 et ref a 3 const, qui sont toutes valides. 
想学习sql的执行流程的可以看博主的另一篇关于sql执行流程的文章哦。 有的同学有疑问了,那最左原则没有用了吗? 答案:有用的。
现在我们说下第3、4、5条sql 第3条: explain select * from employees where age=15 and name='张三'; sql在执行的时候,优化器替我们把索引的顺序优化了,由 age -> name 变成 name -> age,这时 索引是生效的。 第4条: explain select * from employees where position='北京' and name='张三'; 索引顺序优化为name - > position,但是这时索引只有name索引生效,position没有生效,因为我 们建立的索引顺序是 name -> age - > position,你会发现跳过了age,索引本质也是一棵树,少 了一个节点,下面的索引当然不会生效了,这就没有满足最左原则法则。 第5条: explain select * from employees where position='北京' and age=15; 这就和第4条sql一样的道理了,第一个索引都不见了,后面的不可能生效。 执行结果如下:
 Vous pouvez constater que la valeur du troisième type SQL est ref, l'octet est 126 et ref a 2 const, qui sont tous efficaces.
Vous pouvez constater que la valeur du troisième type SQL est ref, l'octet est 126 et ref a 2 const, qui sont tous efficaces.
Le 4ème sql ne fait que 122 octets et la ref n'a qu'1 const, seul l'index du nom prend effet. 
Article 5 La valeur du type sql est all, les bytes et ref sont vides, et tous sont invalides. 
下面说第6条sql,剩下的sql都是和之前的sql一样的道理。 explain select * from employees where position='北京' and age>15 and name='张三'; 这条sql我们会发现,把索引字段全部使用了并且当作条件查询,不一样的是age是范围查找,优化器替我 们把索引顺序优化成 name -> age - > position ,按照我们索引优化第2条:在列上做计算索引失效,范围之后的索引全部失效,想必答案同学们都知道了。 执行结果如下:
 Le 6ème sql ne fait que 126 octets et la valeur du type est plage, recherche par plage, seuls les index de nom et d'âge prennent effet.
Le 6ème sql ne fait que 126 octets et la valeur du type est plage, recherche par plage, seuls les index de nom et d'âge prennent effet.
 Apprentissage recommandé :
Apprentissage recommandé :
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Parlons des bases de la requête de connexion MySQL
- Parlons du niveau d'isolement atteint par les transactions MySQL et MVCC
- Explication détaillée de la véritable méthode d'ouverture de MySql Group par fonction !
- Après avoir lu, comprenez la persistance et la restauration de MySQL (explication détaillée avec images et texte)
- Que faire si centos mysqld ne démarre pas

