Comprendre tous les points de connaissance de l'index MySQL dans un seul article (recommandé de collecter)

Cet article vous apporte les connaissances pertinentes sur l'indexation dans la base de données MySQL, qui contient presque tous les points de connaissance de l'indexation. J'espère qu'il sera utile à tout le monde.

Mysql index

Introduction à l'index

Qu'est-ce que l'index

• Introduction officielle L'index est une structure de données qui aide MySQLobtenir des données efficacement. Pour le dire plus généralement, un index de base de données est comme la table des matières au début d'un livre, qui peut accélérer les requêtes dans la base de données.

• D'une manière générale, l'index lui-même est également très volumineux et il est impossible de tout stocker en mémoire, donc les index sont souvent stockés dans des fichiers sur le disque (peuvent être stockés dans un fichier d'index séparé, ou avec les données stockées dans le fichier de données).

• Ce que nous appelons habituellement les index incluent les index clusterisés, les index couvrants, les index combinés, les index préfixes, les index uniques, etc. Sans instructions spéciales, la valeur par défaut est d'utiliser une structure arborescente B+ (arbre de recherche multi-chemins, pas nécessairement est un index binaire).

Avantages et inconvénients de l'index

Avantages :

• peut améliorer l'efficacité de la récupération des données et réduire le coût d'E/S de la base de données, similaire à la table des matières d'un livre.

• Triez les données via des colonnes d'index, réduisant ainsi le coût du tri des données et la consommation du processeur.

  • Les colonnes indexées seront automatiquement triées, y compris [index de colonne unique] et [index combiné], mais le tri de l'index combiné est plus compliqué.
  • Si vous triez selon l'ordre des colonnes d'index, l'efficacité sera grandement améliorée pour l'ordre par instruction.

Inconvénients :

• L'index occupera de l'espace disque

• Bien que l'index améliore l'efficacité des requêtes, il réduira l'efficacité de la mise à jour de la table. Par exemple, chaque fois qu'une table est ajoutée, supprimée ou modifiée, MySQL doit non seulement sauvegarder les données, mais également sauvegarder ou mettre à jour le fichier d'index correspondant.

Type d'index

Index de clé primaire

Les valeurs de la colonne d'index doivent être uniques, aucune valeur nulle n'est autorisée.

Index normal

Le type d'index de base dans MySQL, sans restrictions, permet d'insérer des valeurs en double et des valeurs nulles dans les colonnes où l'index est défini.

Index unique

Les valeurs de la colonne d'index doivent être uniques, mais les valeurs nulles sont autorisées.

Index de texte intégral

L'index de texte intégral ne peut être créé que sur les champs de type texte CHAR, VARCHAR et TEXT. Lorsque la longueur du champ est relativement grande, si vous créez un index normal, il sera moins efficace lors de l'exécution de requêtes floues. Dans ce cas, vous pouvez créer un index de texte intégral. Les index de texte intégral peuvent être utilisés à la fois dans MyISAM et InnoDB.

Index spatial

MySQL prend en charge les index spatiaux dans les versions ultérieures à 5.7 et prend en charge le modèle de données géométriques OpenGIS. MySQL suit les règles du modèle de données géométriques OpenGIS en termes d'indexation spatiale.

Index de préfixe

Lors de la création d'un index sur des colonnes de type texte telles que CHAR, VARCHAR et TEXT, vous pouvez spécifier la longueur de la colonne d'index, mais vous ne pouvez pas spécifier le type numérique.

Autres (classés en fonction du nombre de colonnes d'index)

1. Index à colonne unique

2. Index combiné

   L'utilisation de l'index combiné doit suivre le principe de correspondance du préfixe le plus à gauche (principe de correspondance le plus à gauche). Généralement, les index combinés sont utilisés à la place de plusieurs index à colonne unique lorsque les conditions le permettent.

Structure de données indexées

Table de hachage

La table de hachage, HashMap et TreeMap en Java sont des structures de table de hachage qui stockent les données sous la forme de paires clé-valeur. Nous utilisons une table de hachage pour stocker les données de la table. Key peut stocker des colonnes d'index et Value peut stocker des enregistrements de lignes ou des adresses de disque de lignes. Les tables de hachage sont très efficaces dans les requêtes équivalentes, avec une complexité temporelle de O(1). Cependant, elles ne prennent pas en charge les recherches de plage rapides et les recherches de plage ne peuvent être effectuées qu'en parcourant la table entière ;

Évidemment, cela ne convient pas pour une utilisation comme index de base de données qui nécessite souvent des recherches et des recherches par plage.

Arbre de recherche binaire

Arbre binaire, je pense que tout le monde aura une image en tête.

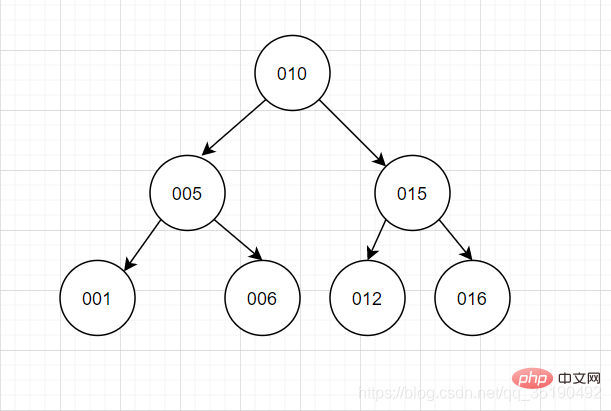
Caractéristiques des arbres binaires : chaque nœud a jusqu'à 2 forks, et l'ordre des données du sous-arbre gauche et du sous-arbre droit est plus petit à gauche et plus grand à droite.

Cette fonctionnalité vise à garantir que chaque recherche peut être réduite de moitié et à réduire le nombre de fois IO. Cependant, l'arbre binaire est un test de la valeur du premier nœud racine, car il nous est facile d'avoir la situation de concurrence qui est la suivante. se produit sous cette fonctionnalité. "L'arbre ne peut pas être fourchu", c'est très inconfortable et instable.

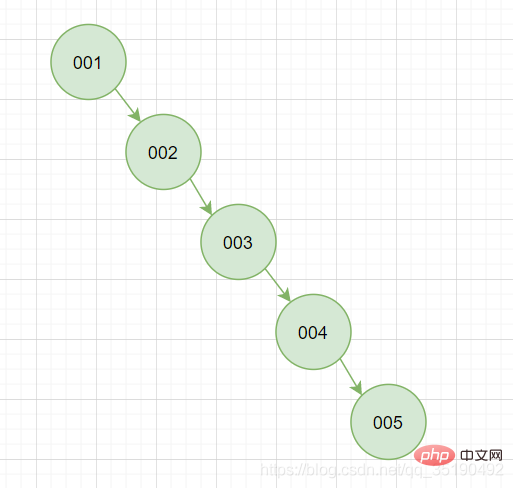
Évidemment, cette situation est instable et nous éviterons certainement cette situation dans la conception

Arbre binaire équilibré

L'arbre binaire équilibré adopte une pensée dichotomique En plus d'avoir les caractéristiques d'un arbre binaire, un arbre de recherche binaire équilibré. , la caractéristique la plus importante est que les niveaux des sous-arbres gauche et droit de l'arbre diffèrent d'au plus 1. Lors de l'insertion et de la suppression de données, l'opération de virage à gauche/à droite est utilisée pour maintenir l'équilibre de l'arbre binaire. Le sous-arbre de gauche ne sera pas très grand et le sous-arbre de droite sera court.

Les performances de la requête utilisant un arbre de recherche binaire équilibré sont proches de la méthode de recherche binaire et la complexité temporelle est O(log2n). L’interrogation de id=6 ne nécessite que deux IO.

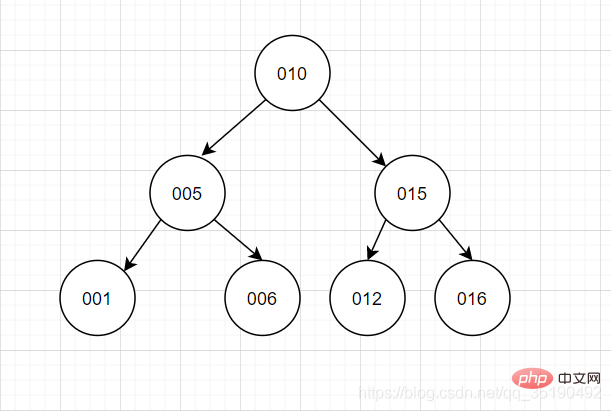
En regardant cette fonctionnalité, vous penserez peut-être que c'est très bien et peut atteindre la situation idéale d'un arbre binaire. Cependant, quelques problèmes subsistent :

1. La complexité temporelle est liée à la hauteur des arbres. L'arborescence doit être récupérée autant de fois que haut, et la lecture de chaque nœud correspond à une opération d'E/S disque. La hauteur de l'arborescence est égale au nombre d'opérations d'E/S disque à chaque fois que des données sont interrogées. Le temps de recherche de chaque disque est de 10 ms. Lorsque la quantité de données de table est importante, les performances des requêtes seront très médiocres. (1 million de volumes de données, log2n est approximativement égal à 20 fois d'E/S disque, temps 20*10=0,2s)

2. L'arbre binaire équilibré ne prend pas en charge la requête de plage pour une recherche rapide. La requête de plage nécessite plusieurs traversées à partir du nœud racine. efficacité des requêtes Pas élevé.

B-Tree : Transformation d'un arbre binaire

Les données MySQL sont stockées dans des fichiers de disque. Lors de l'interrogation et du traitement des données, vous devez d'abord charger les données du disque dans la mémoire. Les opérations d'E/S du disque prennent beaucoup de temps. nous avons donc optimisé le but est de minimiser les opérations d'E/S disque. L'accès à chaque nœud de l'arborescence binaire provoquera une IO. Si vous souhaitez réduire les opérations d'E/S disque, vous devez réduire autant que possible la hauteur de l'arborescence. Alors comment réduire la hauteur de l’arbre ?

Si la clé est bigint=8 octets, chaque nœud a deux pointeurs, chaque pointeur fait 4 octets et un nœud occupe 16 octets d'espace (8+4*2=16).

Parce que le moteur de stockage InnoDB de MySQL lira la quantité de données d'une page (la page par défaut est de 16 Ko) dans une IO, alors que la quantité effective de données dans une IO d'un arbre binaire n'est que de 16 octets, et l'utilisation de l'espace est extrêmement faible. Afin de maximiser l'utilisation d'un espace IO, une idée simple consiste à stocker plusieurs éléments dans chaque nœud et à stocker autant de données que possible dans chaque nœud. Chaque nœud peut stocker 1000 index (16k/16=1000), transformant ainsi l'arbre binaire en un arbre à plusieurs fourches, en augmentant l'arbre à fourches de l'arbre, l'arbre passe de grand et mince à court et gros. Pour construire 1 million de données, la hauteur de l'arborescence n'a besoin que de 2 niveaux (1000*1000=1 million), ce qui signifie que seulement 2 E/S disque sont nécessaires pour interroger les données. Le nombre d'E/S disque est réduit et l'efficacité de l'interrogation des données est améliorée.

Nous appelons cette structure de données un B-tree. Le B-tree est un arbre de recherche équilibré à plusieurs fourchettes, comme indiqué ci-dessous. Les principales caractéristiques sont les suivantes :

1. Les nœuds du B-tree stockent plusieurs éléments. , et chaque nœud interne a plusieurs éléments Forks.

2. Les éléments du nœud contiennent des valeurs clés​​et des données. Les valeurs clés​​dans le nœud sont classées de grande à petite. En d’autres termes, les données sont stockées sur tous les nœuds.

3. Les éléments du nœud parent n'apparaîtront pas dans les nœuds enfants.

4. Tous les nœuds feuilles sont situés sur le même calque, les nœuds feuilles ont la même profondeur et il n'y a pas de connexions de pointeur entre les nœuds feuilles.

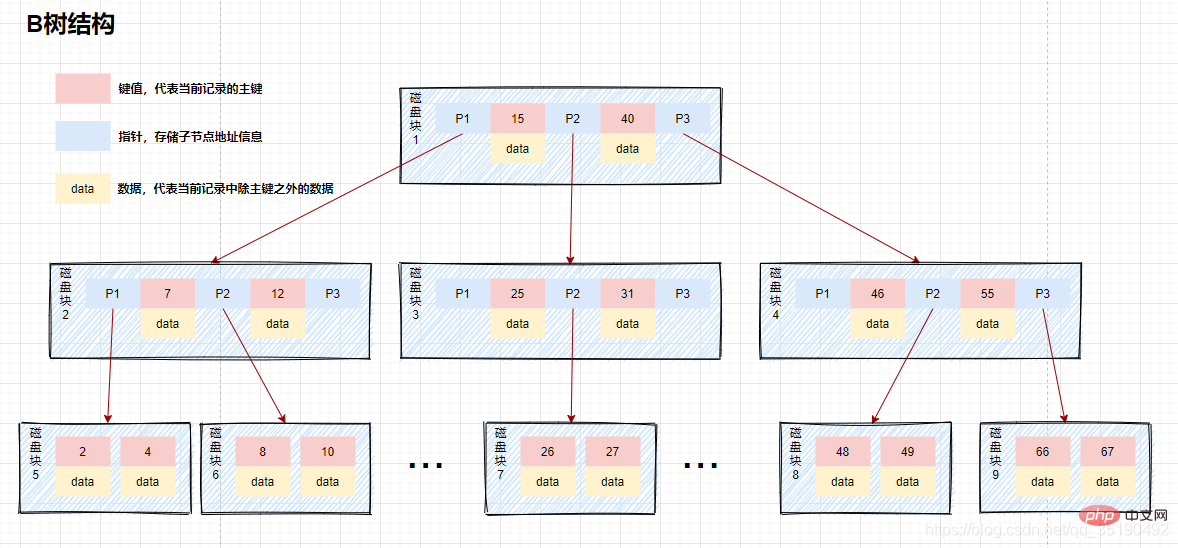
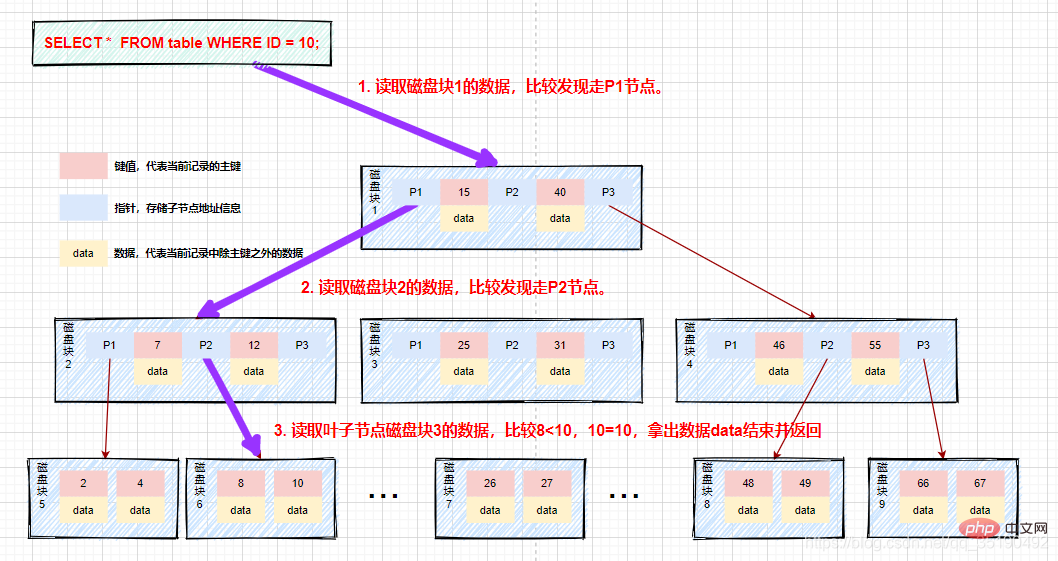
Par exemple, lors de l'interrogation de données dans un b-tree :

Supposons que nous interrogions des données avec une valeur égale à 10. Chemin de requête bloc de disque 1 -> bloc de disque 2 -> bloc de disque 5.

Premier E/S du disque : chargez le bloc de disque 1 en mémoire, parcourez et comparez en mémoire depuis le début, 10

Deuxième disque IO : chargez le bloc de disque 2 en mémoire, parcourez et comparez en mémoire depuis le début, 7

Le troisième disque IO : chargez le bloc de disque 5 dans la mémoire, parcourez et comparez dans la mémoire depuis le début, 10 = 10, trouvez 10, retirez les données, si l'enregistrement de ligne stocké dans les données est supprimé, le la requête se termine. Si l'adresse du disque est stockée, les données doivent être récupérées du disque en fonction de l'adresse du disque et la requête est terminée.

Par rapport à l'arbre de recherche binaire équilibré, pendant tout le processus de recherche, bien que le nombre de comparaisons de données ne soit pas significativement réduit, le nombre d'E/S disque sera considérablement réduit. En même temps, puisque notre comparaison est effectuée en mémoire, le temps de comparaison est négligeable. La hauteur du B-tree est généralement de 2 à 3 couches, ce qui peut répondre à la plupart des scénarios d'application, donc l'utilisation du B-tree pour créer un index peut considérablement améliorer l'efficacité des requêtes.

Le processus est tel que montré sur l'image :

En voyant cela, vous devez penser que le B-tree est idéal, mais les seniors vous diront qu'il y a encore des endroits qui peuvent être optimisés :

1. B-tree ne prend pas en charge la vitesse de recherche par plage, pensez à cette situation. Si nous voulons rechercher des données entre 10 et 35, après avoir trouvé 15, nous devons revenir au nœud racine et parcourir à nouveau la recherche. pour traverser plusieurs fois à partir du nœud racine, et l'efficacité des requêtes doit être améliorée.

2. Si les données stockent des enregistrements de lignes, la taille des lignes augmentera à mesure que le nombre de colonnes augmentera et l'espace occupé augmentera. À ce stade, la quantité de données pouvant être stockées dans une page diminuera, l’arborescence deviendra plus haute et le nombre d’E/S disque augmentera.

Arbre B+ : Transformer l'arbre B

Arbre B+, en tant que version améliorée de l'arbre B, basée sur l'arbre B, MySQL continue de se transformer en fonction de l'arbre B et utilise l'arbre B+ pour créer des index. La principale différence entre un arbre B+ et un arbre B réside dans la question de savoir si les nœuds non-feuilles stockent des données

• Arbre B : les nœuds non-feuilles et les nœuds-feuilles stockent des données.
• Arbre B+ : seuls les nœuds feuilles stockent les données et les nœuds non-feuilles stockent les valeurs clés. Les nœuds feuilles sont connectés à l'aide de pointeurs bidirectionnels, et les nœuds feuilles les plus bas forment une liste chaînée ordonnée bidirectionnelle.

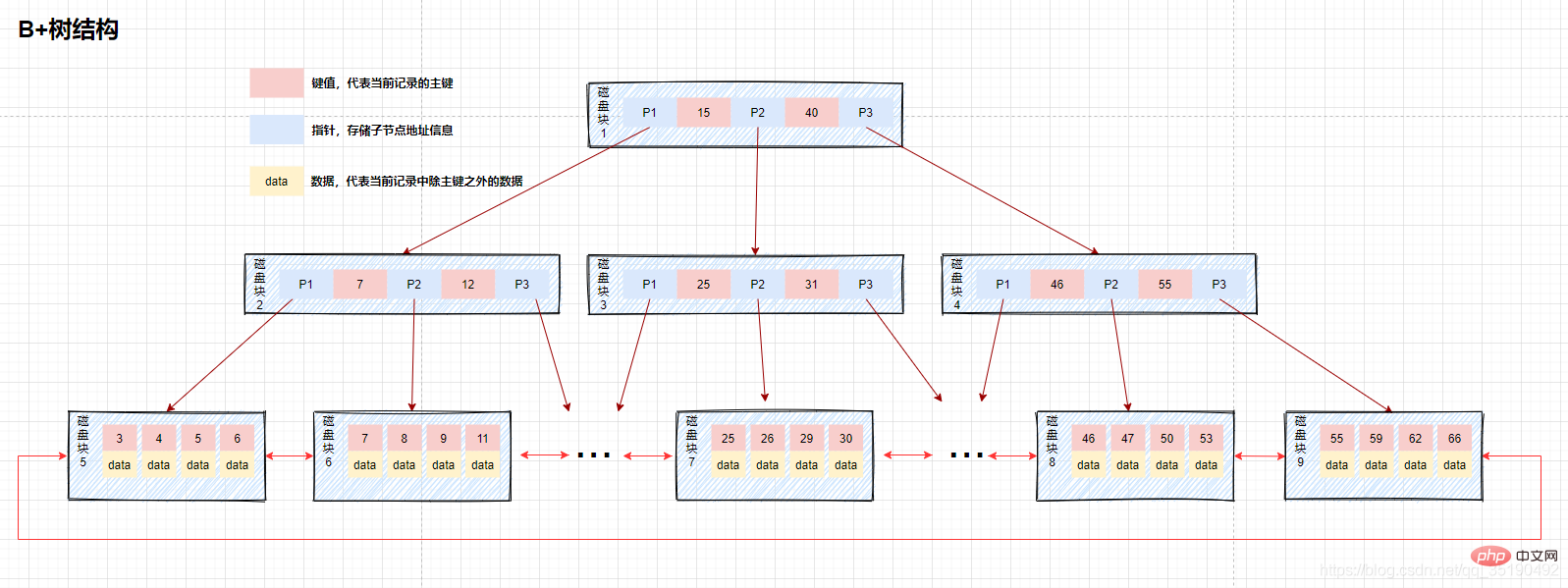
Le nœud feuille le plus bas de l'arbre B+ contient tous les éléments d'index. Comme le montre la figure, lorsque l'arbre B+ recherche des données, puisque les données sont stockées sur le nœud feuille le plus bas, chaque recherche doit récupérer le nœud feuille pour interroger les données. Par conséquent, lorsque des données doivent être interrogées, chaque E/S de disque est directement liée à la hauteur de l'arborescence. Mais d'un autre côté, puisque les données sont placées dans des nœuds feuilles, le nombre d'index stockés dans le bloc disque de l'index est verrouillé. est Il augmentera avec cela, donc par rapport à l'arbre B, la hauteur de l'arbre B+ est théoriquement plus courte que l'arbre B. Il existe également des cas où l'index couvre la requête.Les données de l'index satisfont toutes les données requises par l'instruction de requête actuelle. Dans ce cas, il vous suffit de trouver l'index à renvoyer immédiatement, sans récupérer le nœud feuille le plus bas.

Par exemple :

• Requête équivalente :

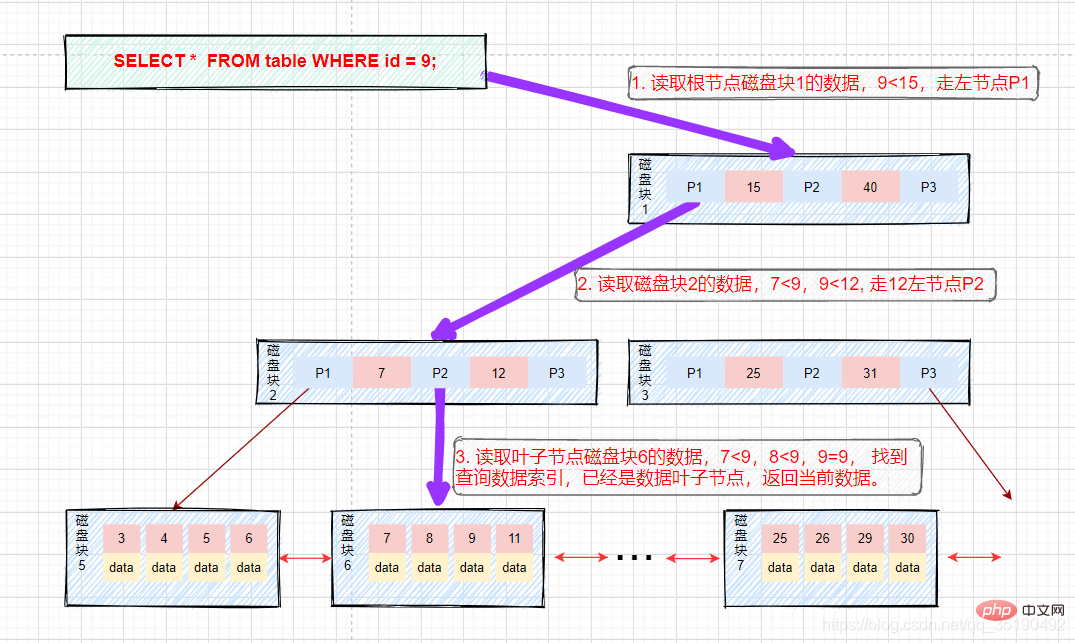
Supposons que nous interrogeons des données avec une valeur égale à 9. Chemin de requête bloc de disque 1 -> bloc de disque 2 -> bloc de disque 6.

1. Premier E/S du disque : chargez le bloc de disque 1 en mémoire, parcourez et comparez en mémoire depuis le début, 9

2. Deuxième IO de disque : chargez le bloc de disque 2 en mémoire, parcourez et comparez en mémoire depuis le début, 7

3. Le troisième disque IO : chargez le bloc de disque 6 dans la mémoire, parcourez et comparez dans la mémoire depuis le début, trouvez 9 dans le troisième index, retirez les données, si l'enregistrement de ligne stocké dans les données est supprimé, la requête se termine. Si l'adresse du disque est stockée, les données doivent être récupérées du disque en fonction de l'adresse du disque et la requête est terminée. (Ce qu'il faut distinguer ici, c'est que Data dans InnoDB stocke les données de ligne, tandis que MyIsam stocke les adresses de disque.) Le processus est comme le montre la figure :

Requête de plage :

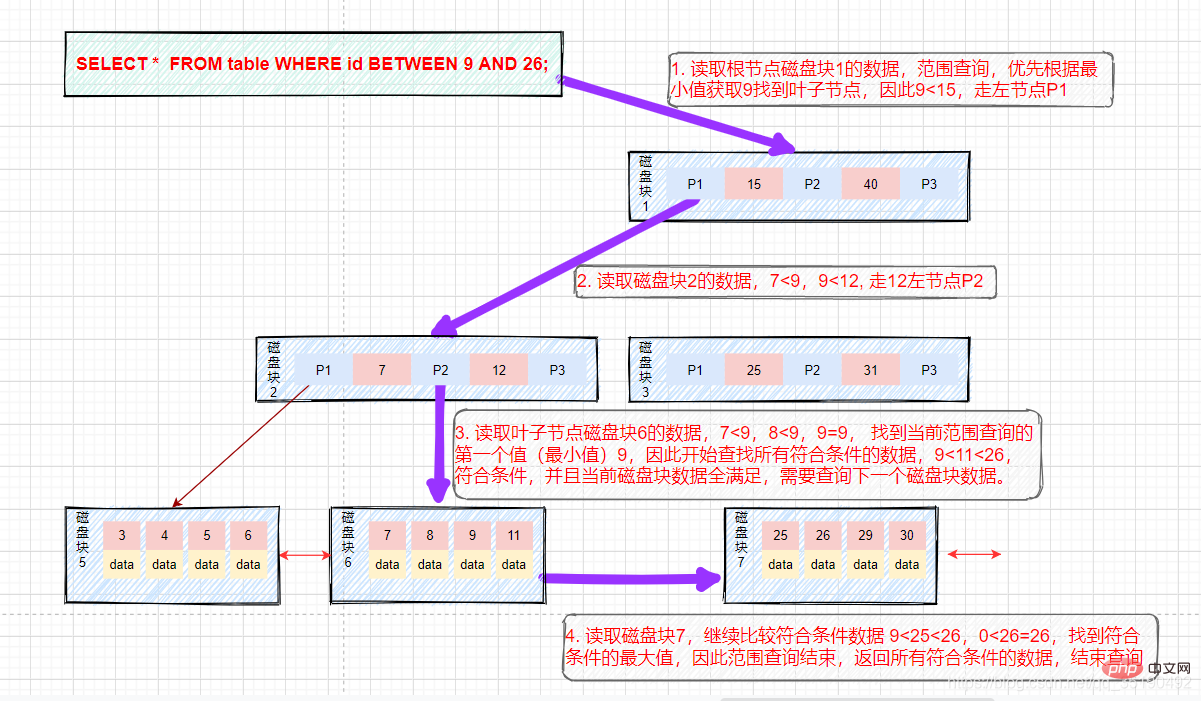
• Supposons que nous souhaitez trouver des données entre 9 et 26. Le chemin de recherche est le bloc de disque 1 -> bloc de disque 2 -> bloc de disque 6 -> bloc de disque 7.

Recherchez d'abord les données avec une valeur égale à 9 et mettez en cache les données avec une valeur égale à 9 dans l'ensemble de résultats. Cette étape est la même que le processus de requête équivalent précédent et trois E/S disque se produisent.

1. Après avoir trouvé 15, le nœud feuille sous-jacent est une liste ordonnée. Nous partons du bloc de disque 6 et de la valeur clé 9 et parcourons en arrière pour filtrer toutes les données qui répondent aux conditions de filtrage.

2. Le quatrième disque IO : adressez et localisez le bloc de disque 7 en fonction du pointeur successeur du disque 6, chargez le disque 7 dans la mémoire, parcourez et comparez dans la mémoire depuis le début, 9

3. La clé primaire est unique (il n'y aura pas

Vous pouvez voir que l'arborescence B+ peut garantir une recherche rapide des requêtes d'égalité et de plage. L'index de MySQL utilise la structure de données de l'arborescence B+.

Implémentation de l'index MySQLAprès avoir introduit la structure des données d'index, elle doit être importée dans Mysql pour voir le scénario d'utilisation réel, voici donc une analyse de l'implémentation de l'index des deux moteurs de stockage de Mysql :

MyISAM index

et

InnoDB Index

MyIsam IndexPrenons une simple table utilisateur comme exemple. Il y a deux index dans la table user, la colonne id est l'index de clé primaire et la colonne age est l'index ordinaire

CREATE TABLE `user`(
  `id`       int(11) NOT NULL AUTO_INCREMENT,
  `username` varchar(20) DEFAULT NULL,
  `age`      int(11)     DEFAULT NULL,
  PRIMARY KEY (`id`) USING BTREE,
  KEY `idx_age` (`age`) USING BTREE) ENGINE = MyISAM  AUTO_INCREMENT = 1
  DEFAULT CHARSET = utf8;

Les fichiers de données et les fichiers d'index de MyISAM sont stockés séparément. Lorsque MyISAM utilise l'arborescence B+ pour créer une arborescence d'index, la valeur de clé stockée dans le nœud feuille est la valeur de la colonne d'index et les données sont l'adresse disque de la ligne où se trouve l'index.

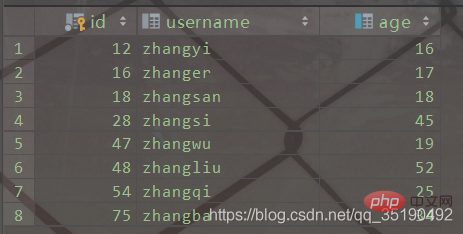Index de clé primaire

L'index de l'utilisateur de la table est stocké dans le fichier d'index

.

Une analyse simple de la situation des E/S du disque lors de la requête :

user.MYI中，数据文件存储在数据文件 user.MYD

Requête de données basée sur les équivalents de clé primaire :

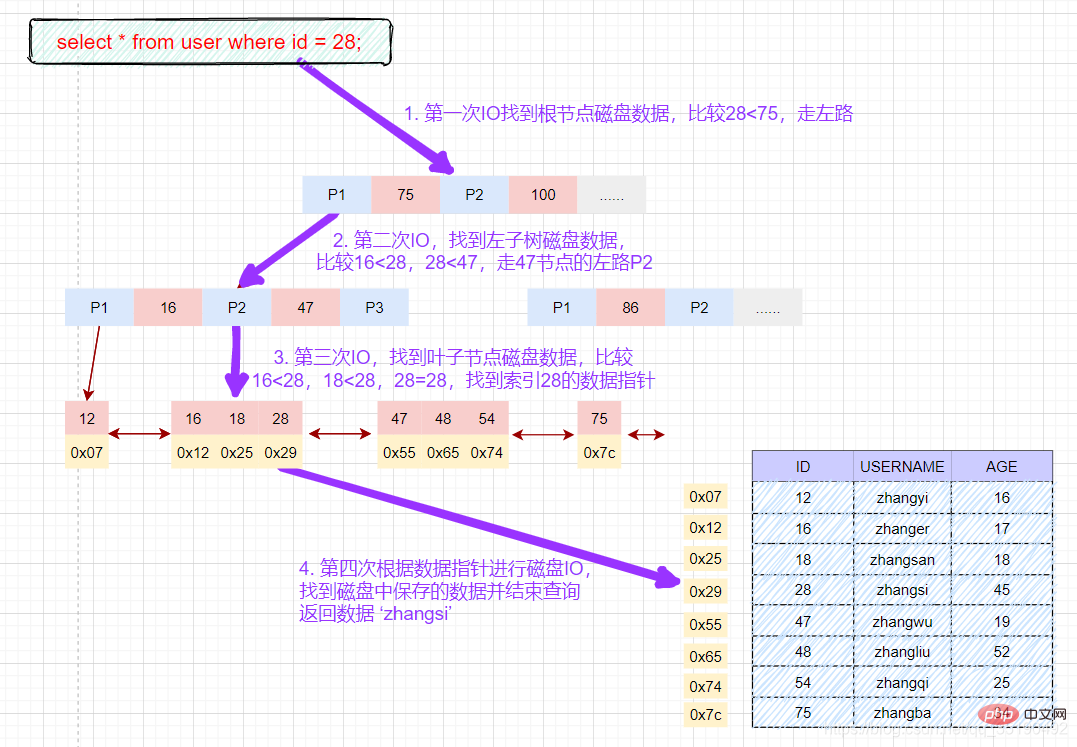
select * from user where id = 28;

1. 先在主键树中从根节点开始检索，将根节点加载到内存，比较28
2. 将左子树节点加载到内存中，比较16
3. 检索到叶节点，将节点加载到内存中遍历，比较16
4. 从索引项中获取磁盘地址，然后到数据文件user.MYD中获取对应整行记录。（1次磁盘IO）
5. 将记录返给客户端。

磁盘IO次数：3次索引检索+记录数据检索。

根据主键范围查询数据：

select * from user where id between 28 and 47;

1. 先在主键树中从根节点开始检索，将根节点加载到内存，比较28

2. 将左子树节点加载到内存中，比较16

3. 检索到叶节点，将节点加载到内存中遍历比较16

   根据磁盘地址从数据文件中获取行记录缓存到结果集中。（1次磁盘IO）

   我们的查询语句时范围查找，需要向后遍历底层叶子链表，直至到达最后一个不满足筛选条件。

4. 向后遍历底层叶子链表，将下一个节点加载到内存中，遍历比较，28

5. 最后得到两条符合筛选条件，将查询结果集返给客户端。

磁盘IO次数：4次索引检索+记录数据检索。

**备注：**以上分析仅供参考，MyISAM在查询时，会将索引节点缓存在MySQL缓存中，而数据缓存依赖于操作系统自身的缓存，所以并不是每次都是走的磁盘，这里只是为了分析索引的使用过程。

辅助索引

在 MyISAM 中,辅助索引和主键索引的结构是一样的，没有任何区别，叶子节点的数据存储的都是行记录的磁盘地址。只是主键索引的键值是唯一的，而辅助索引的键值可以重复。

查询数据时，由于辅助索引的键值不唯一，可能存在多个拥有相同的记录，所以即使是等值查询，也需要按照范围查询的方式在辅助索引树中检索数据。

InnoDB索引

主键索引（聚簇索引）

每个InnoDB表都有一个聚簇索引 ，聚簇索引使用B+树构建，叶子节点存储的数据是整行记录。一般情况下，聚簇索引等同于主键索引，当一个表没有创建主键索引时，InnoDB会自动创建一个ROWID字段来构建聚簇索引。InnoDB创建索引的具体规则如下：

1. 在表上定义主键PRIMARY KEY，InnoDB将主键索引用作聚簇索引。
2. 如果表没有定义主键，InnoDB会选择第一个不为NULL的唯一索引列用作聚簇索引。
3. 如果以上两个都没有，InnoDB 会使用一个6 字节长整型的隐式字段 ROWID字段构建聚簇索引。该ROWID字段会在插入新行时自动递增。

除聚簇索引之外的所有索引都称为辅助索引。在中InnoDB，辅助索引中的叶子节点存储的数据是该行的主键值都。 在检索时，InnoDB使用此主键值在聚簇索引中搜索行记录。

这里以user_innodb为例，user_innodb的id列为主键，age列为普通索引。

CREATE TABLE `user_innodb`(
  `id`       int(11) NOT NULL AUTO_INCREMENT,
  `username` varchar(20) DEFAULT NULL,
  `age`      int(11)     DEFAULT NULL,
  PRIMARY KEY (`id`) USING BTREE,
  KEY `idx_age` (`age`) USING BTREE) ENGINE = InnoDB;

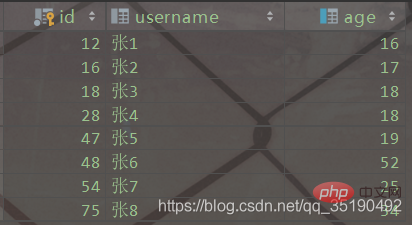
InnoDB的数据和索引存储在一个文件t_user_innodb.ibd中。InnoDB的数据组织方式，是聚簇索引。

主键索引的叶子节点会存储数据行，辅助索引只会存储主键值。

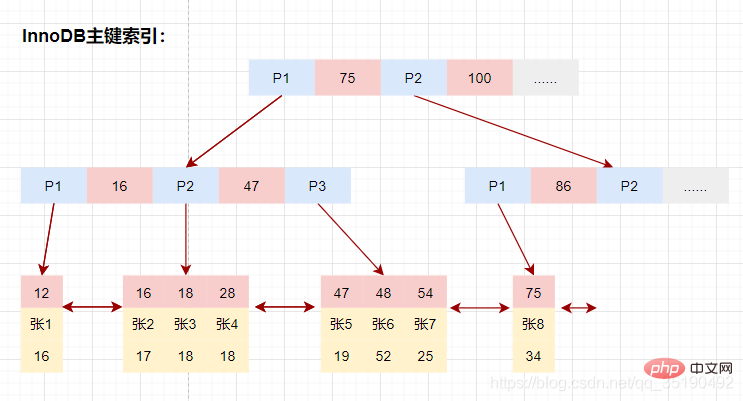
等值查询数据：

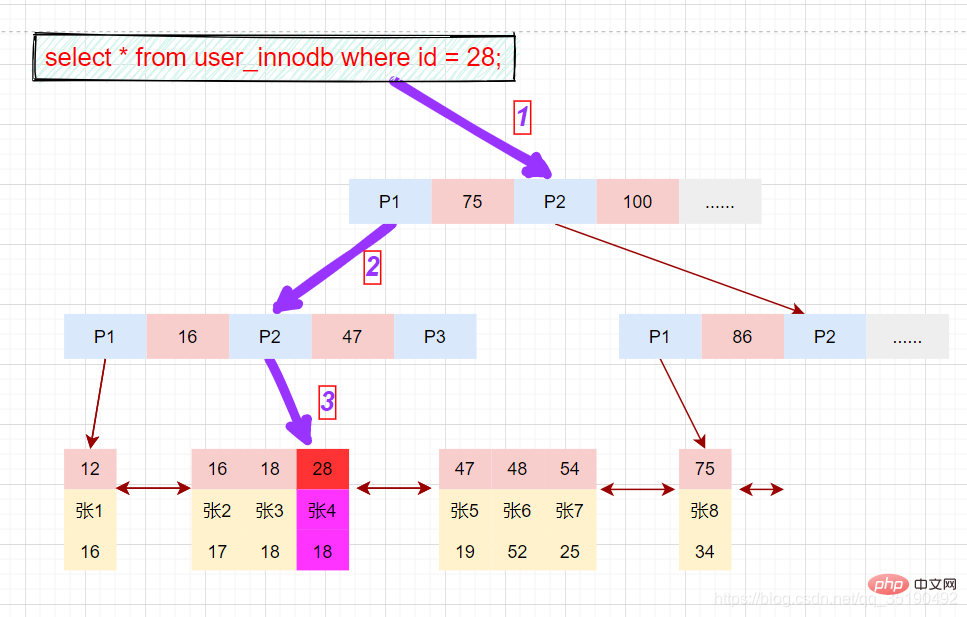
select * from user_innodb where id = 28;

1. 先在主键树中从根节点开始检索，将根节点加载到内存，比较28

2. 将左子树节点加载到内存中，比较16

3. 检索到叶节点，将节点加载到内存中遍历，比较16

   磁盘IO数量：3次。

辅助索引

除聚簇索引之外的所有索引都称为辅助索引，InnoDB的辅助索引只会存储主键值而非磁盘地址。

以表user_innodb的age列为例，age索引的索引结果如下图。

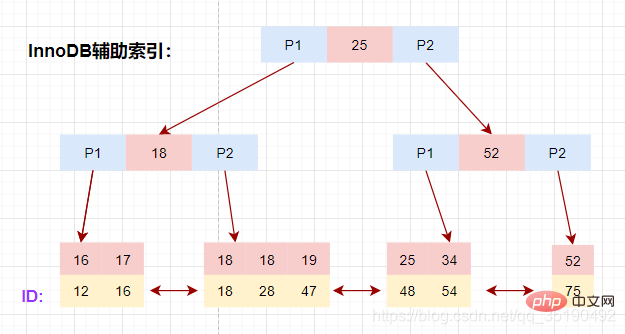
底层叶子节点的按照（age，id）的顺序排序，先按照age列从小到大排序，age列相同时按照id列从小到大排序。

使用辅助索引需要检索两遍索引：首先检索辅助索引获得主键，然后使用主键到主索引中检索获得记录。

画图分析等值查询的情况：

select * from t_user_innodb where age=19;

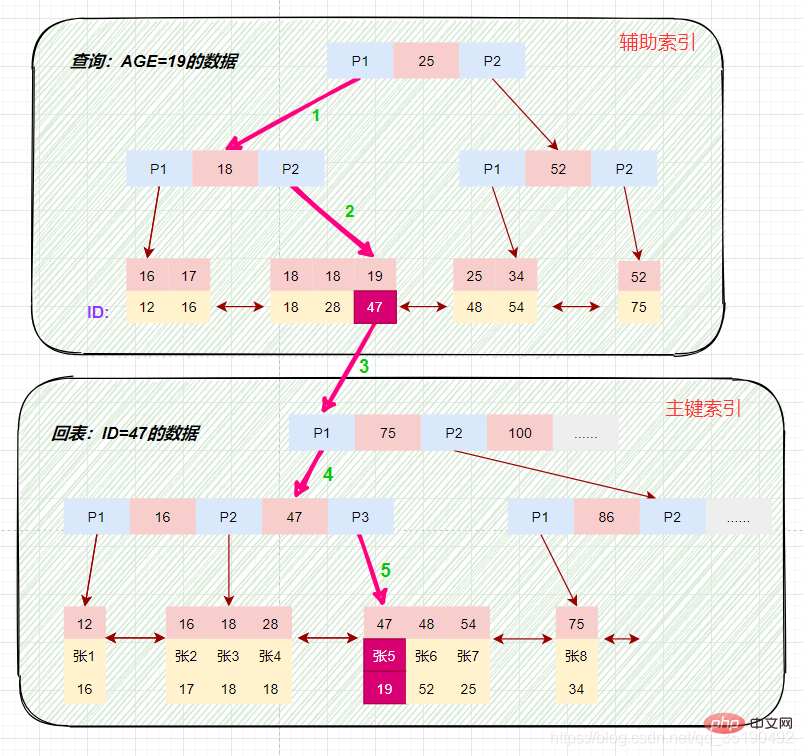
根据在辅助索引树中获取的主键id，到主键索引树检索数据的过程称为回表查询。

磁盘IO数：辅助索引3次+获取记录回表3次

组合索引

还是以自己创建的一个表为例：表 abc_innodb，id为主键索引，创建了一个联合索引idx_abc(a,b,c)。

CREATE TABLE `abc_innodb`(
  `id` int(11) NOT NULL AUTO_INCREMENT,
  `a`  int(11)     DEFAULT NULL,
  `b`  int(11)     DEFAULT NULL,
  `c`  varchar(10) DEFAULT NULL,
  `d`  varchar(10) DEFAULT NULL,
  PRIMARY KEY (`id`) USING BTREE,
  KEY `idx_abc` (`a`, `b`, `c`)) ENGINE = InnoDB;

select * from abc_innodb order by a, b, c, id;

组合索引的数据结构：

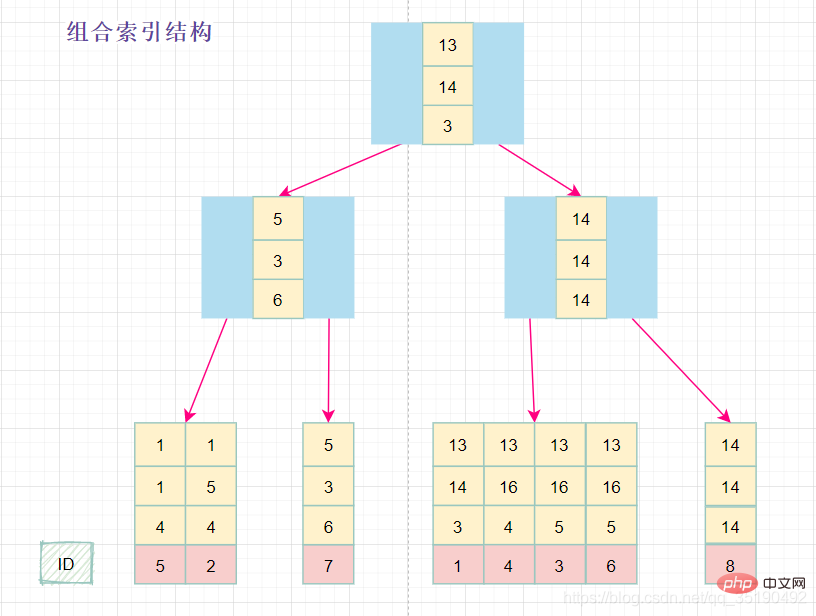
组合索引的查询过程：

select * from abc_innodb where a = 13 and b = 16 and c = 4;

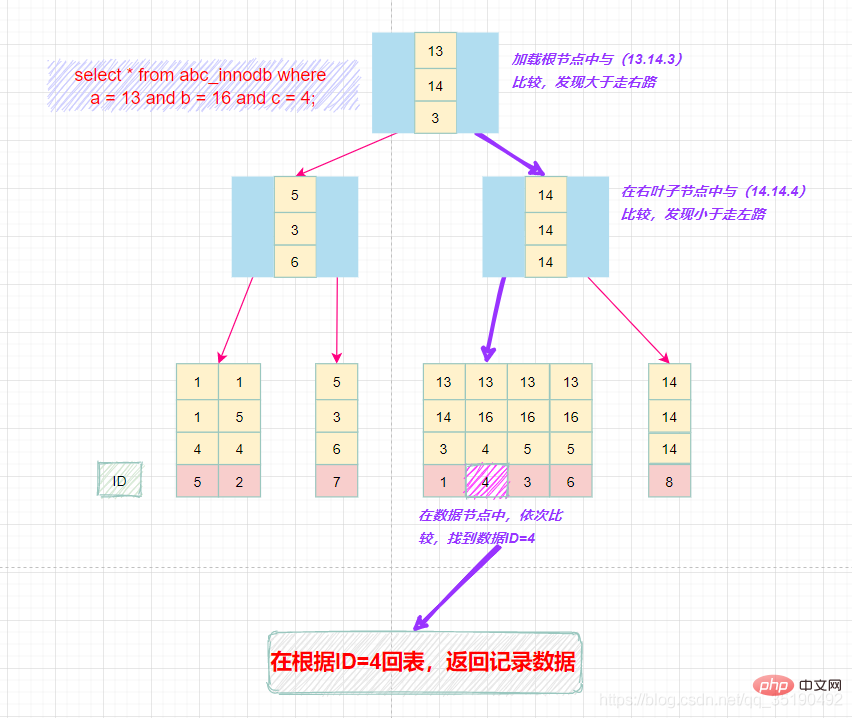
最左匹配原则：

最左前缀匹配原则和联合索引的索引存储结构和检索方式是有关系的。

在组合索引树中，最底层的叶子节点按照第一列a列从左到右递增排列，但是b列和c列是无序的，b列只有在a列值相等的情况下小范围内递增有序，而c列只能在a，b两列相等的情况下小范围内递增有序。

就像上面的查询，B+树会先比较a列来确定下一步应该搜索的方向，往左还是往右。如果a列相同再比较b列。但是如果查询条件没有a列，B+树就不知道第一步应该从哪个节点查起。

可以说创建的idx_abc(a,b,c)索引，相当于创建了(a)、（a,b）（a,b,c）三个索引。、

组合索引的最左前缀匹配原则：使用组合索引查询时，mysql会一直向右匹配直至遇到范围查询(>、

覆盖索引

覆盖索引并不是说是索引结构，覆盖索引是一种很常用的优化手段。因为在使用辅助索引的时候，我们只可以拿到主键值，相当于获取数据还需要再根据主键查询主键索引再获取到数据。但是试想下这么一种情况，在上面abc_innodb表中的组合索引查询时，如果我只需要abc字段的，那是不是意味着我们查询到组合索引的叶子节点就可以直接返回了，而不需要回表。这种情况就是覆盖索引。

可以看一下执行计划：

覆盖索引的情况：

未使用到覆盖索引：

总结

看到这里，你是不是对于自己的sql语句里面的索引的有了更多优化想法呢。比如：

避免回表

在InnoDB的存储引擎中，使用辅助索引查询的时候，因为辅助索引叶子节点保存的数据不是当前记录的数据而是当前记录的主键索引，索引如果需要获取当前记录完整数据就必然需要根据主键值从主键索引继续查询。这个过程我们成位回表。想想回表必然是会消耗性能影响性能。那如何避免呢？

使用索引覆盖，举个例子：现有User表（id(PK),name(key),sex,address,hobby…）

Si dans un scénario, select id,name,sex from user where name ='zhangsan';Cette instruction est fréquemment utilisée en entreprise, et les autres champs de la table utilisateur sont utilisés beaucoup moins fréquemment qu'elle. Dans ce cas, si nous construisons l'index du champ nom, au lieu d'utiliser un seul index. , mais utilisez l'index conjoint (nom, sexe). Dans ce cas, si vous exécutez à nouveau cette instruction de requête, vous pouvez obtenir les données complètes de l'instruction actuelle en fonction des résultats de la requête d'index auxiliaire. Cela peut effectivement éviter de revenir à la table pour obtenir des données sur le sexe.

Voici une stratégie d'optimisation typique utilisant un index de couverture pour réduire le dos de la table.

L'utilisation de l'index conjoint

index conjointLors de la création d'un index, essayez de juger si un index conjoint peut être utilisé sur plusieurs index à une seule colonne. L'utilisation d'index conjoints permet non seulement d'économiser de l'espace, mais facilite également l'utilisation de la couverture d'index. Imaginez, plus il y a de champs indexés, plus il sera facile de satisfaire les données renvoyées par la requête. Par exemple, l'index conjoint (a_b_c) équivaut à avoir trois index : a, a_b, a_b_c. Cela permet-il d'économiser de l'espace ? Bien entendu, l'espace économisé n'est pas trois fois supérieur à celui des trois index (a, a_b, a_b_c). Parce que les données de l'arborescence d'index n'ont pas changé, mais les données du champ de données d'index sont effectivement enregistrées.

Le principe de création d'un index conjoint. Lors de la création d'un index conjoint, les colonnes fréquemment utilisées et les colonnes avec une discrimination élevée doivent être placées devant. Une utilisation fréquente signifie une utilisation élevée de l'index, et une discrimination élevée signifie une grande granularité de filtrage. tous les scénarios d'optimisation qui doivent être pris en compte lors de la création d'un index. Vous pouvez également ajouter des champs qui sont souvent renvoyés sous forme de requêtes à l'index conjoint et utiliser un index de couverture, alors je recommande cette situation. Utilisez l’index commun ci-dessous.

Utilisation de l'index conjoint

1. Déterminez s'il existe déjà plusieurs index à une seule colonne qui peuvent être fusionnés. Si tel est le cas, créez un index conjoint à partir des multiples index à une seule colonne actuels.

2. L'index actuel contient des colonnes fréquemment utilisées comme champs de retour. À ce stade, vous pouvez déterminer si la colonne actuelle peut être ajoutée à l'index existant afin que l'instruction de requête puisse utiliser l'index de couverture.

【Recommandé : tutoriel vidéo mysql】

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!