Quelle est l'image en php ? Comment peut-on le stocker ?

Avec l’approfondissement des apprentissages, nos connaissances s’élargissent et s’enrichissent constamment. La structure arborescente a-t-elle dérouté tout le monde ? Croyez-moi, après avoir appris le diagramme, vous sentirez que les arbres binaires sont tout simplement d'une simplicité indescriptible. En fait, l’arbre dont nous parlons est aussi une forme particulière de graphique.

Le concept des images

Vous souvenez-vous encore de l'image d'un arbre que nous avons vue dans le premier article sur l'apprentissage des arbres ?

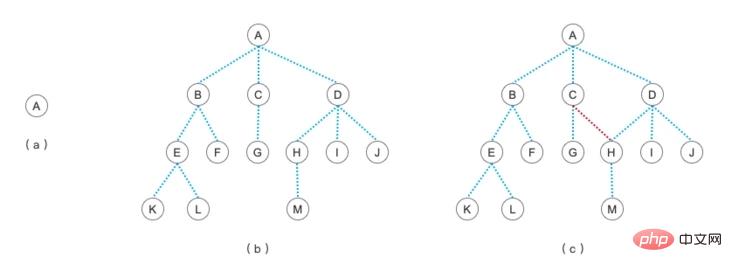
A cette époque, on disait que l'image c n'est pas un arbre, mais une image. Pourquoi? D’après la définition de l’arbre, nous pouvons voir qu’un arbre ne peut avoir qu’un seul nœud racine, qu’il ne peut y avoir aucune connexion entre les niveaux et qu’il peut avoir plusieurs nœuds enfants. Les graphiques ne doivent pas nécessairement suivre ces règles. La caractéristique des graphiques est que les nœuds peuvent être connectés les uns aux autres. Par exemple, les images ci-dessous sont toutes des images.

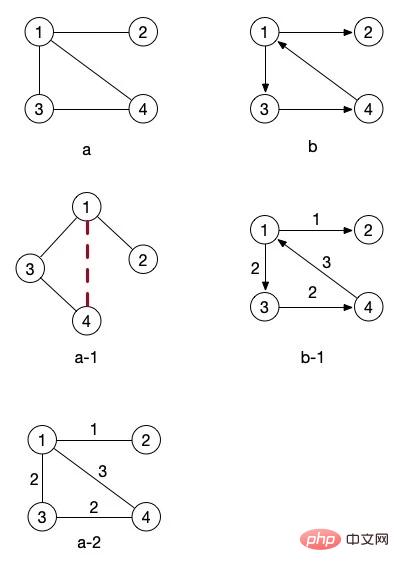
Dans l'image dessinée ci-dessus, l'image b a une flèche, tandis que la ligne de connexion de l'image a n'a pas de flèche. Une image avec une direction claire comme celle-ci est appelée un graphe orienté. Un graphe sans flèches, c’est-à-dire sans direction, est appelé graphe non orienté.

Portons d’abord notre attention sur la figure a-1. En fait, elle fait simplement pivoter la figure a. Est-ce que tout le monde peut le voir ? Si vous ignorez la connexion entre les nœuds 4 et 1, alors c'est un arbre. Est-ce cohérent avec le concept de la figure c dans notre arborescence ci-dessus ?

La définition officielle la plus formelle du graphe est :

Le graphe G se compose de deux ensembles V et E, notés G=(V, E), où V est un ensemble fini non vide de sommets, E est un ensemble fini de sommets dans V, et ces sommets sont également appelés arêtes.

Dans un graphique orienté, le segment de ligne reliant deux points du nœud de départ au nœud de pointage peut être enregistré sous la forme . et sont deux côtés différents, qui peuvent également être appelés arcs. D'après la figure a, nous pouvons voir qu'il y a , 1> , , Dans la figure b, comme il s'agit d'un graphe orienté, il n'a que quatre arêtes : , , , .

Vous sentez que c'est plus clair lorsque vous regardez l'image ci-dessus, mais vous êtes confus lorsque vous regardez cette définition ? Si vous êtes un étudiant qui doit passer un test, vous devez quand même mémoriser cette définition. Si vous souhaitez simplement vous concentrer sur l’apprentissage, l’application ou la compréhension comme moi, il n’est pas nécessaire de le mémoriser par cœur. V est le nœud et E est la relation entre ces nœuds. La relation entre deux sommets, c'est-à-dire que les segments de ligne reliant les nœuds sur le graphique sont les arêtes.

OK, maintenant que ces trois concepts les plus fondamentaux sont compris, continuons à apprendre d'autres terminologies liées aux images !

Termes liés aux graphiques

Tout d'abord, nous utilisons n pour représenter le nombre de sommets dans le graphique, et e pour représenter le nombre d'arêtes. Rappelez-vous ces deux codes.

• (1) Sous-graphe : Supposons qu'il y ait deux graphes G=(V, E) et G'=(V', E') Si V' est contenu dans V et E' est contenu dans E, on l'appelle G' est le sous-graphe de G

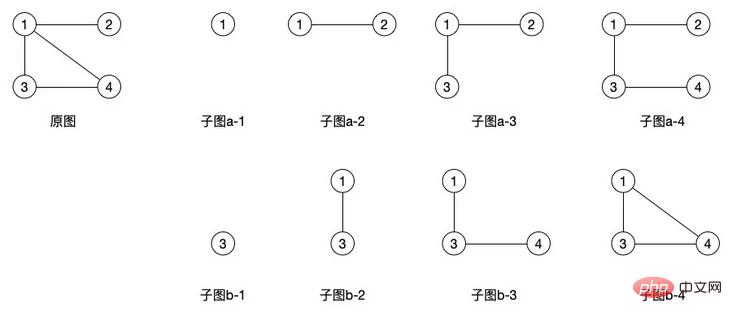
Les sous-graphes à droite dans l'image ci-dessus sont tous des sous-graphes du graphe original. On peut voir que les sous-graphes peuvent produire de nombreuses formes. Le même concept est utilisé pour les graphes orientés. , mais Par rapport aux graphes non orientés, les graphes orientés peuvent générer moins de sous-graphes car leurs arêtes sont directionnelles.

• (2) Graphique complet non orienté et graphe complet orienté : Pour un graphe non orienté, s'il a n(n-1)/2 arêtes, c'est un graphe complet non orienté. Pour un graphe orienté, s’il a n(n-1) orphelins, on l’appelle un graphe complet orienté. (Reportez-vous à l'arbre binaire complet)

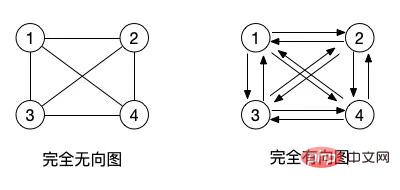
En fait, le concept d'un graphe complet est que tous les nœuds adjacents du graphe ont des arêtes qui peuvent les relier entre eux.

Pour les graphiques orientés, bien que les arêtes aient des directions, nous pouvons bien sûr également définir une direction de va-et-vient, telle que et . dessiner Les deux flèches en sens inverse ci-dessus indiquent qu'il peut aller de 1 à 2 ou de 2 à 1. Dans les graphiques non orientés, une arête est utilisée pour remplacer le concept de ces deux arêtes. L'arête sans direction de flèche est bidirectionnelle.

• (3) Graphe clairsemé et graphe dense : Un graphe avec peu d'arêtes ou d'orphelins (comme e

• (4) Quanhe.com : dans les applications pratiques, chaque bord ou île peut être marqué d'une valeur qui a une certaine signification, tout comme la distance sur une carte. Ces valeurs sont appelées poids. Une image avec autorité peut être appelée un réseau

Les chiffres sur les côtés de la figure a-2 et de la figure b-1 dans les images du haut représentent les poids. Ces deux images peuvent être appelées images de réseau. Nous apprendrons la notion de poids plus tard lorsque nous parlerons des algorithmes associés. À partir de ces deux images, nous pouvons effectivement voir clairement que si nous voulons passer du nœud 1 au nœud 4, nous n'allons pas directement à côté, mais il est plus rapide de prendre l'itinéraire

• (5) Points adjacents : Deux nœuds avec des arêtes sont des points adjacents

• (6) Degré, degré intérieur et degré extérieur : Le degré d'un sommet v fait référence au nombre d'arêtes associées à v. Pour un graphique orienté, la flèche pointant vers d'autres nœuds est le degré sortant, et la flèche pointant vers elle-même est le degré entrant

Continuons à regarder la figure b. Le nœud 1 a deux diplômes sortants et un diplôme entrant. Cela ne semble pas nécessiter beaucoup d’explications.

• (7) Chemin et longueur du chemin : Tous les sommets passant d'un sommet à un autre sommet sont des chemins. S’il s’agit d’un graphe orienté, alors son chemin est dans le sens de la flèche. La longueur du chemin est le nombre d'arêtes ou d'orphelins qui passent sur un chemin

• (8) Boucle ou boucle : Un chemin dont le premier sommet et le dernier sommet sont identiques est appelé une boucle ou une boucle

• (9) connectés, connectés Graphiques et composants connectés : S'il existe un chemin entre deux nœuds, ils sont dits connectés. Si tous les nœuds du graphe entier peuvent être connectés les uns aux autres, alors le graphe est un graphe connecté. Un composant connexe est un sous-graphe connexe maximal dans un graphe non orienté.

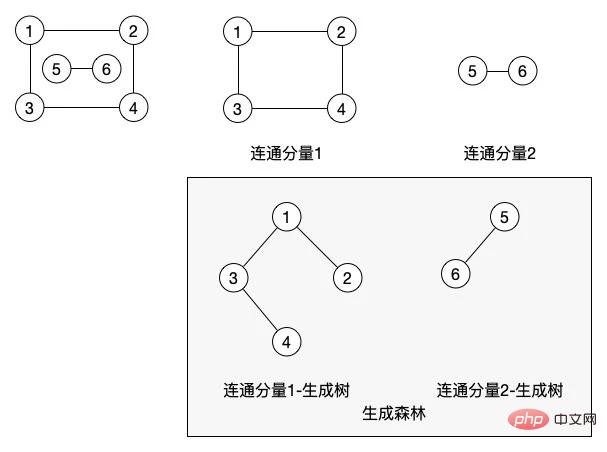
Les trois concepts suivants sont également donnés dans cette image. Dans un graphe non orienté, une composante connexe est égale à un sous-graphe connexe maximal. Dans ce graphe, nous avons deux composantes connexes.

• (10) Sous-graphe connecté maximum : le nombre maximum de nœuds qu'un sous-graphe connecté peut contenir. Si un nœud supplémentaire est ajouté, le sous-graphe ne sera pas un graphe connecté

• (11) Arbre couvrant : un A. Le sous-graphe connecté minimal contient tous les sommets du graphe, mais seulement n-1 arêtes suffisantes pour former un arbre. Un tel sous-graphe connecté est l'arbre couvrant d'un graphe connecté

En fait, via un chemin, il peut. Laissez tous les nœuds du graphique être connectés en série. Dans le graphique des composants connectés, nous générons deux arbres couvrants minimum basés sur les deux composants connectés. Les nœuds du spanning tree de leur composant connecté 1 ne doivent pas nécessairement être dans cette structure. Nous pouvons mettre le nœud 4 sous le nœud 2, selon la manière dont nous parcourons pour générer ce spanning tree minimum.

L'arbre couvrant minimum de notre image du haut a peut en fait être la figure a-1 sans la ligne pointillée rouge. Bien entendu, le nœud 4 peut également être placé sous le nœud 1. Cela dépend également de la manière dont notre programme parcourt le graphique pour générer quel type d'arbre.

• (12) Forêt couvrante : Dans un graphe non connecté, chaque composant connecté peut générer un arbre couvrant connecté, qui constitue la forêt couvrant l'ensemble du graphe non connecté

Êtes-vous confus après avoir lu ceci ? Ce n’est pas grave, nous utiliserons fréquemment ces termes dans des études ultérieures, et celle-ci n’est pas la plus complète. Vous pouvez utiliser la bibliographie et d’autres supports d’apprentissage pour approfondir et comprendre la terminologie liée aux graphiques.

Résumé

Le concept de graphiques est presque introduit. Vous pouvez le digérer et continuer à étudier le contenu suivant. Ce n'est que le début. De nombreux étudiants auront le sentiment que cette chose s'est beaucoup améliorée par rapport à la structure arborescente. N'ayez pas peur, après avoir acquis les connaissances suivantes, même si vous n'avez pas encore compris le contenu lié au graphique, vous aurez certainement une compréhension plus profonde de la structure arborescente. Pourquoi? Les arbres sont en fait des graphiques sans boucles. Leur parcours se fait en profondeur ou en largeur, mais le graphique est plus compliqué. Maintenant, pensez-vous qu’il y a encore un peu d’espoir pour l’avenir ? L’apprentissage est souvent un processus progressif. Il y aura toujours un lien entre les connaissances actuelles et les connaissances passées. Ne réfléchissez pas trop d’abord, avancez simplement étape par étape !

Recommandé : "Résumé des questions d'entretien PHP 2021 (collection)" "Tutoriel vidéo PHP"

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!