Que sont les arbres binaires complets et les arbres binaires indicés ? Quelle est leur structure de stockage séquentielle ?

Dans le dernier article, nous avons appris la structure de base de la chaîne des arbres binaires et les opérations liées à la construction et au parcours des arbres. Aujourd'hui, nous apprenons quelques concepts liés aux arbres binaires et à une forme modifiée d'arbres binaires.

Arbre binaire complet

Qu'est-ce qu'un arbre binaire complet ? Avant de parler d'arbres binaires complets, parlons d'un autre terme : « arbres binaires complets ». Comme l’arbre binaire que nous avons démontré dans notre article précédent, il s’agit d’un « arbre binaire complet ». Dans cet arbre, tous les nœuds ont deux nœuds enfants, aucun nœud n'a un seul nœud enfant et tous les nœuds feuilles les plus bas sont au même niveau. Ce type d'arbre est appelé " " Arbre binaire complet ", également connu sous le nom de " Arbre binaire parfait ". Arbre".

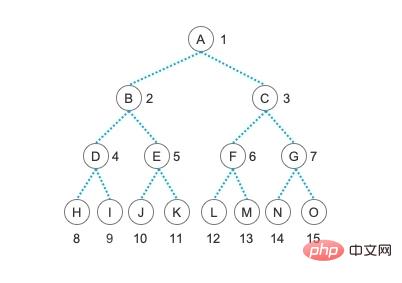
N'est-ce pas un très bel arbre ? Oui, ce type d'arbre binaire est très parfait. Il n'a pas de nœuds supplémentaires ni de nœuds manquants. Il est très beau. Cependant, en réalité, les choses parfaites sont très rares et il y aura toujours des défauts dans la vie. Nous essayons de ne pas nous laisser trop de défauts, mais nous ne pouvons jamais vivre une vie sans défauts. Par conséquent, nous permettons aux nœuds feuilles d'apparaître au niveau le plus bas et au niveau inférieur suivant, et les nœuds feuilles au niveau le plus bas sont concentrés dans la partie gauche de l'arborescence, c'est-à-dire que les nœuds feuilles ne peuvent avoir que des sous-arbres gauches. un tel arbre manque légèrement. L'arbre est appelé un "arbre binaire complet". Ne vous inquiétez pas qu'elle ne soit pas parfaite, car une vie aussi légèrement imparfaite est complète, donc « l'arbre binaire complet » est une structure arborescente idéale.

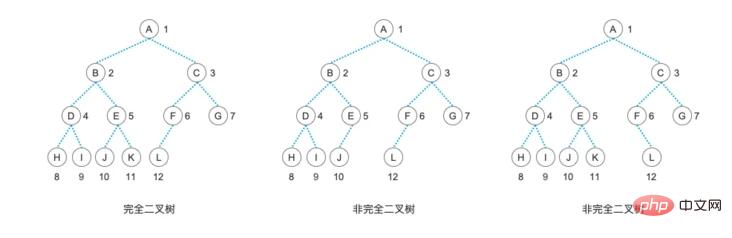
D'après la définition, nous pouvons voir qu'un "arbre binaire complet" doit être un "arbre binaire complet", et un nœud feuille est sur un seul niveau et tous les nœuds ont des enfants gauche et droit. "L'arbre" sur lequel vous cliquez est également un "arbre binaire complet".

Pourquoi parle-t-on d'« arbre binaire complet » et d'« arbre binaire complet » ? Bien sûr, il s’agit d’ouvrir la voie à notre prochain contenu. Parce qu'un « arbre binaire complet » est un arbre qui se conforme le mieux aux propriétés d'un arbre binaire. Vous souvenez-vous encore des cinq propriétés des arbres binaires présentées dans le premier article de la série des arbres ? A cette époque, nous utilisions « l'arbre binaire complet » comme exemple pour expliquer. Parmi elles, la propriété 5 est la base pour nous permettre d'apprendre à utiliser des structures séquentielles pour stocker des arbres binaires.

Stockage séquentiel des arbres binaires

Grâce au concept d'"arbre binaire complet" et à la propriété 5 des arbres binaires, nous pouvons réaliser la mise en œuvre de l'utilisation d'un tableau pour stocker la structure séquentielle.

$treeList = ['', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O'];

Je pense que vous le connaissez. Dans l'article précédent, nous avons utilisé ce tableau pour construire un arbre de chaîne, et ce tableau est en fait un arbre binaire stocké linéairement. Jetons un coup d'œil en comparant la propriété 5 des arbres binaires.

• L'indice du nœud A est 1, qui est la racine de notre arbre. Ses nœuds enfants sont B et C, et les indices correspondants sont respectivement 2 et 3, c'est-à-dire 1 2 et 1 2 + 1.

• De même, nous sélectionnons un autre nœud F. Son indice est 6, donc l'indice de son nœud enfant gauche est 6 2 = 12, correspondant à L ; son nœud enfant droit est 6 2 + 1 = 13, correspondant à M.

• En regardant les choses dans l'autre sens, le nœud parent d'un nœud est i / 2 . Regardons l'indice du nœud K est 11 et son nœud parent est 11/2. Si vous supprimez la virgule décimale, c'est la position de l'indice 5, qui est le nœud E, l'indice du nœud J est 10 ; Le nœud parent est 11/2. Le nœud est 10/2, qui est également le nœud E d'index 5.

Maintenant, je pense que tout le monde comprend comment utiliser un tableau pour représenter une structure arborescente binaire. De plus, la structure du tableau est plus unidimensionnelle, ce qui peut mieux refléter le fait que le fonctionnement de l'arbre est une représentation bidimensionnelle unidimensionnelle, c'est-à-dire une conversion non linéaire en linéaire, afin que nous puissions facilement exploiter ces éléments. données.

Pour les structures de stockage séquentielles, c'est-à-dire le parcours des éléments du tableau, vous pouvez également utiliser l'ordre pré-ordre, intermédiaire, post-ordre et hiérarchique. Cependant, ces méthodes de parcours doivent être parcourues conformément à la propriété 5 des arbres binaires. Mais plus important encore, tant que vous me donnez un indice, grâce aux propriétés d'un arbre binaire, nous pouvons facilement connaître les positions de ses nœuds subordonnés et supérieurs, et nous pouvons obtenir rapidement les informations de ces nœuds. Cette fonctionnalité majeure n'est pas disponible dans les arbres binaires structurés en chaîne.

Et si ce que nous voulons stocker n'est pas un « arbre binaire complet » ? Même s'il ne s'agit pas d'un arbre binaire complet, il vous suffit de définir le nœud correspondant sur une valeur nulle. Par exemple :

$treeList = ['', 'A', 'B', 'C', 'D', 'E', 'I', '', '', '', '', 'H', '', 'J', '', ''];

L'arbre binaire correspondant à la structure de cet arbre est comme ceci :

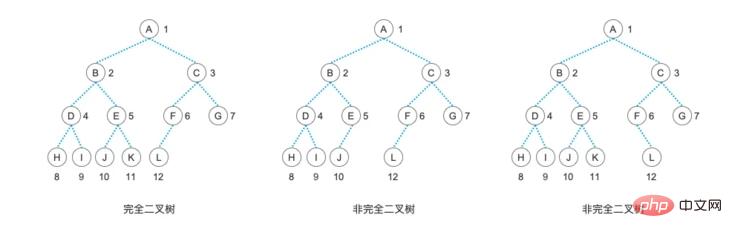
Ensuite, dans la méthode de construction de l'arbre en chaîne, il suffit d'ajouter un jugement supplémentaire. Nous pouvons rapidement générer un arbre binaire enchaîné grâce à un tel arbre binaire stocké séquentiellement, ce qui facilitera nos opérations ultérieures.

// 建立二叉树
function CreateBiTree($arr, $i)
{
    if (!isset($arr[$i]) || !$arr[$i]) { // 这里增加了个判断，如果数组元素为空
        return null;
    }
    $t = new TBTNode();
    $t->data = $arr[$i];
    $t->lChild = CreateBiTree($arr, $i * 2);
    $t->rChild = CreateBiTree($arr, $i * 2 + 1);
    return $t;
}

Clue Binary Tree

Un lien dans un autre, parlons ensuite de «Clue Binary Tree». Qu'est-ce que c'est?

从上面的学习中，我们知道了”满二叉树“和”完全二叉树“。但是这种结构都是非常理想的树结构，不过真实的情况可能大部分都是”理想很丰满，现实很骨感“。很多树并不能形成那样的完全二叉树的形式，更别提”满二叉树“了。而树的遍历又经常会使用栈或者队列来实现，这两种遍历方式基本都是线性的，也就是最好情况下也是 O(n) 的时间复杂度。那么，有没有什么更快一点的方式来提高遍历的效率呢？

我们这样来尝试一下：

• 如果树的叶子结点的左孩子结点为空，就让它指向前驱（上级）结点

• 如果树的叶子结点的右孩子结点为空，就让它指向后继结点

这样有什么好处呢？我们可以避免掉大范围的递归操作，从而加快树的遍历速度。在整个算法中，它并没有什么优势，因为我们需要将一颗树进行线索化，也就是去改变它的叶子结点的左右孩子的指向，这也是一次遍历。但是，如果你的操作是经常需要遍历，而且是来回的多次遍历，那么它的整体性能是要强于普通二叉树的遍历的。因为在一次线索化之后，它的遍历就是在快速的查找叶子结点的基础上进行普通的线性遍历操作，而不是递归操作。

对于线索二叉树来说，我们需要改变树的结点存储数据结构。

// 线索二叉树结点
class TBTNode
{
    public $data;
    public $lTag = 0;
    public $rTag = 0;
    public $lChild;
    public $rChild;
}

我们增加了两个标志位，当 $lTag 或 $rTag 为 1 时，$lChild 或 $rChild 分别指向前驱或后继结点。这样在最后的遍历时，我们就可以快速地通过这个 tag 标志位分辨出结点的指向状态。

然后我们先简单地建立一颗树。使用上一节中的那个示例。

// 建立二叉树
function CreateBiTree($arr, $i)
{
    if (!isset($arr[$i]) || !$arr[$i]) { // 这里增加了个判断，如果数组元素为空
        return null;
    }
    $t = new TBTNode();
    $t->data = $arr[$i];
    $t->lChild = CreateBiTree($arr, $i * 2);
    $t->rChild = CreateBiTree($arr, $i * 2 + 1);
    return $t;
}

$treeList = ['', 'A', 'B', 'C', 'D', 'E', 'I', '', '', '', '', 'H', '', 'J', '', ''];

$tree = CreateBiTree($treeList, 1);

接下来就是最重要的线索化过程，我们可以建立前序、中序、后序的线索二叉树。对应的，在最后的线索二叉树遍历时获得的结果也将是这三种遍历方式所对应的结果。在这里，我们学习最普遍的也是最经典的”中序线索二叉树“。所以，我们以中序遍历的形式将这颗树线索化。

// 线索化
function InThread(?TBTNode $p, ?TBTNode &$pre)
{
    if ($p) {
        // 递归，左子树线索化
        InThread($p->lChild, $pre);

        if (!$p->lChild) {
            // 建立当前结点的前驱线索
            $p->lChild = $pre;
            $p->lTag = 1;
        }
        if ($pre && !$pre->rChild) {
            // 建立当前结点的后继线索
            $pre->rChild = $p;
            $pre->rTag = 1;
        }
        $pre = $p; // $pre 指向当前的 $p ，作为 $p 将要指向的下一个结点的前驱结点指示指针
        $p = $p->rChild; // $p 指向一个新结点，此时 $pre 和 $p 分别指向的结点形成了一个前驱后继对，为下一次线索化做准备
        
        // 递归，右子树线索化
        InThread($p, $pre);
    }
}

// 创建线索二叉树
function createInThread(TBTNode $root)
{
    $pre = null; // 前驱结点指针
    if($root){
        InThread($root, $pre);
        $pre->rChild = null; // 非空二叉树，线索化
        $pre->rTag = 1; // 后处理中序最后一个结点
    }
}

createInThread($tree);

var_dump($tree);
// object(TBTNode)#1 (5) {
//     ["data"]=>
//     string(1) "A"
//     ["lTag"]=>
//     int(0)
//     ["rTag"]=>
//     int(0)
//     ["lChild"]=>
//     object(TBTNode)#2 (5) {
//       ["data"]=>
//       string(1) "B"
//       ["lTag"]=>
//       int(0)
//       ["rTag"]=>
//       int(0)
//       ["lChild"]=>
//       object(TBTNode)#3 (5) {
//         ["data"]=>
//         string(1) "D"
//         ["lTag"]=>
//         int(1)
//         ["rTag"]=>
//         int(1)
//         ["lChild"]=>
//         NULL
//         ["rChild"]=>
//         *RECURSION*
//       }
//       ……

关于算法的具体步骤在注释中已经写得很详细了。一句话总结就是在中序遍历的过程中，根据结点的信息来确定它的左右孩子的形式，如果有左右孩子就继续，如果没有任一一个孩子的话，就将左右结点指向前驱或者后继。建立之后的线索二叉树就如图所示：

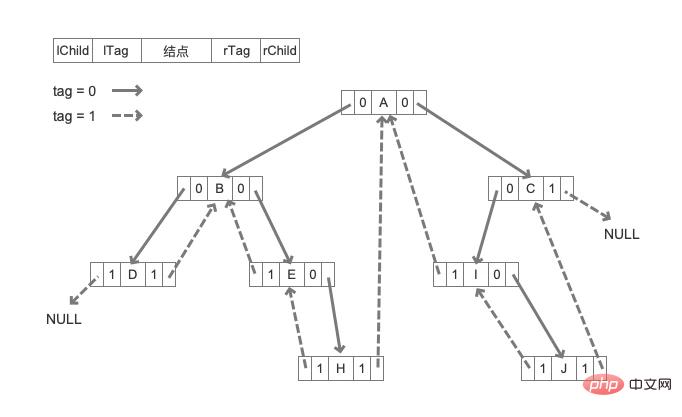
最后就是遍历了。我们需要的是能够快速地获得最左叶子结点的信息，然后就是下一跳的信息，这时，线索的威力就发挥出来了。

// 以 $p 为根的中序线索二叉树中，中序序列下的第一个结点，也就是最左边那个结点
function First(?TBTNode $p){
    while($p->lTag == 0){
        $p = $p->lChild; // 最左下结点（不一定是叶子结点）
    }
    return $p;
}

// 在中序二叉树中，结点 $p 在中序下的后继结点
function NextNode(?TBTNode $p){
    if($p->rTag == 0){
        return First($p->rChild);
    }else{
        return $p->rChild; // 如果 rTag == 1 ，直接返回后继线索
    }
}

// 在中序线索二叉树上进行中序遍历
function Inorder(TBTNode $root){
    //     第一个结点      结点不为空    下一个结点
    for($p = First($root);$p;$p=NextNode($p)){
        echo $p->data, ',';
    }
}

Inorder($tree); // D,B,E,H,A,I,J,C,

当遇到 $lTag 不为 0 的结点时，这个结点就是最左的那个结点了，如果这个不为空的话，【输出】它。接着我们获得下一跳的结点，也就是判断这个结点的右孩子 $rTag 标志，如果是为 0 的，也就是它还有右孩子，【输出】后向下查找，直到找到一个 $rTag 也为 1 的结点，直接返回这个结点的后继，也就是中序遍历的中间那个结点，【输出】它。

最后输出的顺序是不是和我们中序遍历的结果一样呢？注意看代码，在遍历中序线索二叉树的时候，我们没有用一个递归吧，全部是使用的 while() 和 for() 就完成了对这个线索二叉树的遍历。

总结

坚持到现在不容易，不能再小看数据结构了吧？现在还只是树，我们的图都还没开始呢！当然，也不要害怕，一步一步的学，慢慢掌握，不要幻想一口气吃成个胖子。写完这篇文章我也不可能马上就手写出一个中序的线索二叉树来的。大家还是以理解原理为主，如果说真能手写的话，那也是为了面试而去背的或者是为了考研而准备的。这样的小同学在面试中我反而要更多问一些其它的问题，毕竟临时抱佛脚的准备远不如深入理解带来的感悟更能打动人！

测试代码：

https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/4.树/source/4.3完全二叉树、线索二叉树及树的顺序存储结构.php

推荐学习：php视频教程

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!