Maison >développement back-end >tutoriel php >Traversée de graphe de structure de données PHP : la profondeur d'abord et la largeur d'abord
Traversée de graphe de structure de données PHP : la profondeur d'abord et la largeur d'abord
- 藏色散人avant
- 2021-07-01 13:42:082752parcourir
Traversation du graphique : profondeur d'abord et largeur d'abord
La traversée d'arbres a évolué en traversée de graphes
Rappelez-vous que dans l'étude des arbres, nous avons parlé de traversée en pré-ordre, dans l'ordre, après-ordre et par ordre de niveau Quelles sont ces formes de parcours ? En fait, la pré-commande, la mi-commande et la post-commande peuvent être considérées comme une sorte de méthode de parcours. Ils utilisent tous la structure de pile pour parcourir. La caractéristique est d'aller d'abord au chemin noir, puis de revenir au chemin non parcouru. chemin. Le parcours par ordre de couche utilise une file d'attente pour parcourir couche par couche. Sa caractéristique est de parcourir d'abord les nœuds enfants, puis de parcourir les nœuds de niveau suivant de chaque nœud enfant un par un. Après avoir examiné la méthode de parcours d'arbre, il sera très simple d'apprendre la méthode de parcours de graphe, car dans le parcours de graphe, les deux formes de parcours les plus élémentaires sont basées sur la pile et la file d'attente. C'est juste que leurs noms sont légèrement différents. La méthode de parcours basée sur la pile est appelée parcours en profondeur d'abord, tandis que la méthode de parcours basée sur la file d'attente est appelée parcours en largeur en premier. En fait, cela correspond au parcours du premier, du milieu et du dernier ordre et au parcours de l'ordre des couches dans l'arborescence. Il n'y a pas beaucoup de différence en substance. [Recommandé :Tutoriel vidéo PHP]
Traversée en profondeur en premier
Nous traversons toujours à partir de la pile Commencez par la méthode, qui est la forme d'un parcours en profondeur d'abord dans la figure. Pour la pile, les nouveaux nœuds sont continuellement poussés sur la pile jusqu'à ce qu'il s'avère qu'il n'a pas d'autres nœuds enfants, puis le chemin d'origine est renvoyé. Lorsqu'un nœud s'avère avoir d'autres nœuds, le nœud enfant est poussé sur la pile. stack. C'est l'idée du parcours profond. Ici, il convient de noter que nous devons enregistrer les nœuds qui ont été visités. Lorsqu'il existe plusieurs nœuds avec des chemins connectés à un certain nœud, assurez-vous que ce nœud n'a été visité qu'une seule fois. C'est la plus grande différence avec la structure arborescente, car l'arborescence est jusqu'en bas, il n'y a aucune connexion entre les nœuds horizontaux et un nœud n'a qu'un seul nœud supérieur. Dans un graphe, n’importe quel nœud peut être lié à n’importe quel autre nœud.Adjacency Matrix
Tout d'abord, examinons l'implémentation de l'algorithme de parcours en profondeur d'abord pour la matrice d'adjacence. Peu importe si vous ne le comprenez pas maintenant. Faites défiler vers le bas pour voir les illustrations, puis lisez-les ensemble. Bien entendu, une meilleure solution consiste à l’exécuter vous-même.$visited = []; // 已访问结点
function DFS_AM($graphArr, $x)
{
global $visited;
echo "节点:{$x}", PHP_EOL;
$visited[$x] = true; // 当前结点标记为已访问
// y 就是邻接矩阵中的横行
for ($y = 1; $y <= count($graphArr); $y++) {
// 循环判断第 [x][y] 个数据是否为 1,也就是是否有边
// 并且这个结点没有被访问过
if ($graphArr[$x][$y] != 0 && !$visited[$y]) {
// 进行栈递归,传递的参数是当前这个结点
DFS_AM($graphArr, $y);
}
}
}
BuildGraph($graphArr); // 建立邻接矩阵图
echo '请输入开始遍历的结点(1-结点数):';
fscanf(STDIN, "%d", $startNode); // 输入从第几个结点开始访问
DFS_AM($graphArr, $startNode); // 开始深度优先遍历 Ce n'est pas beaucoup de code. J'utilise le code pour établir la matrice de contiguïté de l'article précédent. Si vous l'avez oublié, revenez en arrière ou allez directement au code source. à partir du lien en bas de l'article. Ensuite on teste : # php 5.3图的遍历:深度优先与广度优先.php 输入结点数:4 请输入边数:3 请输入边,格式为 出 入 权:1 2 1 请输入边,格式为 出 入 权:1 3 1 请输入边,格式为 出 入 权:3 4 1 请输入开始遍历的结点(1-结点数):3 节点:3 节点:1 节点:2 节点:4
Liste d'adjacence
Bien sûr, l'idée de parcourir la liste d'adjacence est la même, sauf que la L'algorithme de boucle au milieu est utilisé pour déterminer les caractéristiques de la chaîne.$visited = []; // 已访问结点
function DFS_AL($graph, $x){
global $visited;
$p = $graph->adjList[$x]; // 指定结点的第一个边结点
echo "节点:{$x}", PHP_EOL; // 输出指定结点的信息
$visited[$x] = true; // 设置该结点已被访问
while($p != null){
$y = $p->adjVex; // 获得边结点信息
if(!$visited[$y]){ // 如果结点没有被访问过
DFS_AL($graph, $y); // 进入这个边结点的深度遍历过程
}
$p = $p->nextArc; // 移动到下一个边结点
}
}
$graph = BuildLinkGraph();
$graphBFS = $graph;
echo '请输入开始遍历的结点(1-结点数):';
fscanf(STDIN, "%d", $startNode); // 输入从第几个结点开始访问
DFS_AL($graph, $startNode);// 开始深度优先遍历N'est-ce pas aussi très simple ? Testons-le simplement ensuite : # php 5.3图的遍历:深度优先与广度优先.php 请输入 结点数 边数: 4 3 请输入边,格式为 出 入 权:1 2 1 请输入边,格式为 出 入 权:1 3 1 请输入边,格式为 出 入 权:3 4 1 请输入开始遍历的结点(1-结点数):3 节点:3 节点:4 节点:1 节点:2Pourquoi l'ordre de sortie est-il différent de celui de la matrice de contiguïté ? La liste de contiguïté que nous avons implémentée dans l'article précédent utilise l'interpolation de tête. Les dernières données d'entrée sont ajoutées devant le lien de nœud. Si nous mettons 3 4 1 dans la première entrée, alors le nœud sera le même que la matrice de contiguïté. les résultats du parcours sont les mêmes.
Diagramme de parcours en profondeur d'abord
Je suis venu directement regarder le code et j'ai longuement parlé de l'algorithme. Êtes-vous toujours confus ? Peu importe, regardons directement l'image :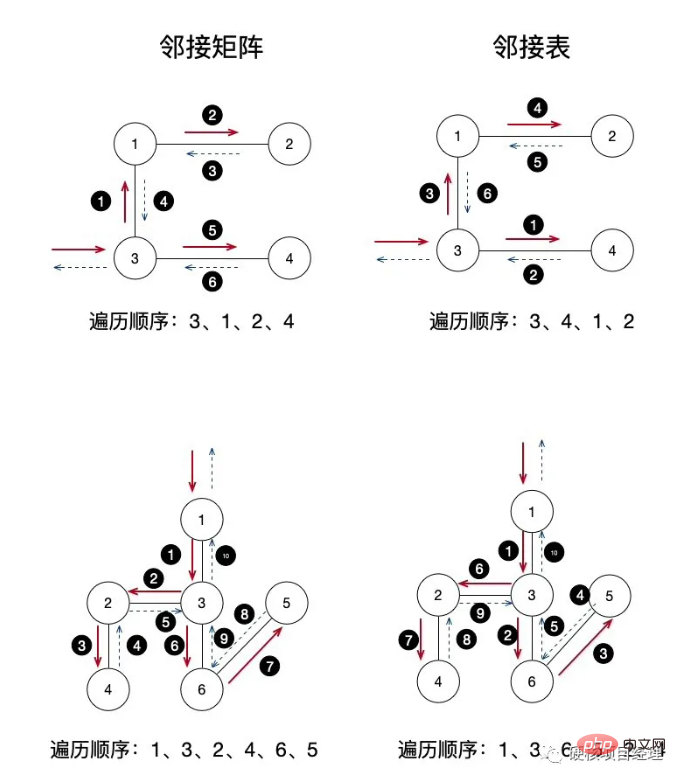
- Nous saisissons d'abord l'accès à partir du nœud 3, puis démarrons la traversée en profondeur, puis générons le résultat Point 3
- Dans la première étape de la boucle du nœud 3, on obtient qu'il a une arête avec le nœud 1, donc le nœud 1 est passé récursivement, et le nœud 1 est poussé sur la pile
- Nœud de sortie 1, le nœud 1 est en haut de la pile dans la récursion actuelle
在 结点1 的循环中发现 结点1 和 结点 2 有边,于是递归传入 结点2 ,结点2 入栈
输出 结点2,目前的递归中 结点2 在栈顶
注意了,重点在这里,结点2 的循环中没有发现与其它未访问的结点有边存在了,于是递归开始返回,也就是开始出栈了,依次返回到 结点1 、结点3,没有任何输出,栈空了,递归回到最外层的函数了
继续 结点3 的循环,发现与 结点4 有边,递归传入 结点4
输出 结点4,目前的递归中 结点4 在栈顶
结点4 的循环中没有发现其它未访问的结点及边了,递归返回,结点4 出栈
结点3 循环完成,遍历结束
一步一步的很清晰吧,大家试着自己分析一下下面那个复杂一些图的深度遍历顺序,看看和我们程序输出的结果是不是一样的。在很多的考研或者数据结构考试中,经常会有选择题或应用题让你手动地来写出深度优先遍历的顺序哦!
广度优先遍历
接下来就是广度优先遍历了,其实说白了就是我们在学习树的遍历时候的层序遍历。前面我们说过,深度遍历是一条路走到黑,没路了退回来。而广度遍历则是一层一层的查看,直到找到出口。
邻接矩阵
使用邻接矩阵来进行广度优先遍历的操作,其实最核心的遍历方式和深度遍历没什么区别,都是对某一个结点进行边的查找,唯一不同的就是把递归栈换成了队列而已。
$visited = [];
function BFS_AM($graphArr, $x){
global $visited;
$queue = InitSqQueue(); // 初始化队列
$graphCount = count($graphArr); // 获取矩阵结点数量
$visited[$x] = true; // 结点标记为已访问
EnSqQueue($queue, $x); // 结点入队
while($x){ // 循环判断结点是否 fasle
// 遍历所有结点是否与这个结点有边
for ($y = 1; $y <= $graphCount; $y++) {
// 如果有边并且未访问过
if ($graphArr[$x][$y] != 0 && !$visited[$y]) {
$visited[$y] = true; // 结点标记为已访问
EnSqQueue($queue, $y); // 结点入队
}
}
$x = DeSqQueue($queue); // 出队一个结点
echo $x, PHP_EOL; // 输出结点
}
}
echo '请输入开始广度遍历的结点(1-结点数):';
fscanf(STDIN, "%d", $startNode);
BFS_AM($graphArr, $startNode); // 开始广度遍历代码中的注释也很清晰明了了,我们直接进行测试:
…… …… 请输入开始广度遍历的结点(1-结点数):3 3 1 4 2
邻接表
同样地,我们也提供邻接表的链式广度优先遍历的核心函数。
$visited = [];
function BFS_AL($graph, $x){
global $visited;
$visited[$x] = true; // 结点标记为已访问
$queue = InitSqQueue();// 初始化队列
EnSqQueue($queue, $x); // 结点入队
// 如果一直有能出队的结点,就一直循环
// 也就是说,如果队列空了,循环就结束
while(($i = DeSqQueue($queue))!==false){
echo $i, PHP_EOL; // 输出结点
$p = $graph->adjList[$i]; // 结点的第一个边结点
while($p != null){ // 如果不为空
$y = $p->adjVex; // 边结点信息
if(!$visited[$y]){ // 如果没有访问过
$visited[$y] = true; // 标记结点为已访问
EnSqQueue($queue, $y); // 入队结点
}
$p = $p->nextArc; // 结点指针指向下一个
}
}
}
echo '请输入开始遍历的结点(1-结点数):';
fscanf(STDIN, "%d", $startNode);
BFS_AL($graph, $startNode); // 开始广度遍历核心的循环中的操作其实也和深度遍历没什么太大的区别,同样是换成了队列这种存储形式而已。
…… …… 请输入开始广度遍历的结点(1-结点数):3 3 4 1 2
广度优先遍历图示
好吧,上面又罗列完了算法,接下来就是图示的时间了,相信还是一看图大家就马上能明白广度优先遍历的具体步骤了。
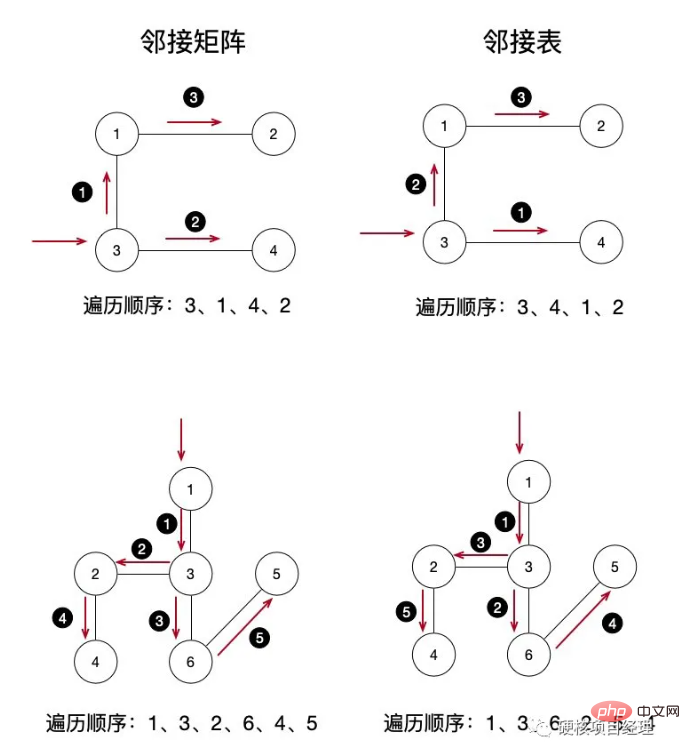
和上面的图一样,同样还是左边是邻接矩阵,右边是邻接表。在这里,我们依然还是直接分步骤来看一下左边最上面图的遍历操作顺序:
输入 结点3 开始广度遍历,结点标记为已访问,这时 结点3 入队
使用 while 循环判断 结点x 是否为 null ,如果不为 null 进入循环体
遍历所有结点是否与这个结点有边,如果有边,并且这个结点没有被访问过,标记已访问,加入队列
出队一个元素,并赋值给 x
输出 x 结点的信息
广度优先遍历没有栈的回溯,就是一条线性的队列走完就完了,所以图示会非常清晰。单独一个结点我们会将和它相关的所有结点入队,然后出队最顶上的结点,这样就能够像树的层序遍历一样按照一层一层的顺序来遍历整个图。同样地,拿起纸笔,找复杂一点的图,试试能不能手写出类似于广度优先遍历顺序的题目吧!
总结
大家学完了之后是不是发现今天介绍的深度优先和广度优先两种遍历方式真的和树的遍历方式没什么太大的区别。最大的不同就是我们要标记已访问过的结点而已。不管怎么说,使用栈和队列来对树或图进行遍历是所有树和图的操作算法中最最基础的部分,也是考试和面试中最常见的问题,大家一定要深入理解掌握哦!
测试代码: https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/5.图/source/5.3图的遍历:深度优先与广度优先.php
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

