Quel est le but de la normalisation des données ?

Le but de la normalisation des données est de limiter les données prétraitées à une certaine plage, éliminant ainsi les effets néfastes causés par des échantillons de données singuliers. Après la normalisation des données, la vitesse de descente du gradient pour trouver la solution optimale peut être accélérée et la précision peut être améliorée (comme KNN).

L'environnement d'exploitation de ce tutoriel : système Windows 7, ordinateur Dell G3.

Dans le domaine de l'apprentissage automatique, différents Indice d'évaluation (c'est-à-dire que différentes caractéristiques du vecteur de caractéristiques sont les différents indices d'évaluation) Avoir souvent des dimensions et des unités dimensionnelles différentes. Cette situation affectera les résultats de l'analyse des données. Afin d'éliminer l'influence dimensionnelle entre les indicateurs, les données doivent être standardisées <.> pour résoudre la comparabilité entre les indicateurs de données. Une fois les données originales traitées par normalisation des données, chaque indicateur est du même ordre de grandeur, ce qui convient à une évaluation comparative complète. Parmi eux, le plus typique est le traitement de normalisation des données . (Vous pouvez vous référer à l'étude : Standardisation/Normalisation des données)

En bref, le but de la normalisation est de limiter les données prétraitées à une certaine plage (telle que [0,1] ou [-1,1]), éliminant ainsi Les effets indésirables causés par d'étranges exemples de données.

1) En statistique, le rôle spécifique de la normalisation est de résumer un échantillon statistique uniforme distribution. La normalisation entre 0 et 1 est une distribution de probabilité statistique et la normalisation entre -1 et +1 est une distribution de coordonnées statistiques.

2) Les données d'échantillon singulières font référence à un vecteur d'échantillon qui est particulièrement grand ou petit par rapport à d'autres entrées. échantillons (c'est-à-dire vecteur de caractéristiques), par exemple, ce qui suit est un exemple de données x1, x2, x3, x4, x5, x6 avec deux caractéristiques (vecteur de caractéristiques -> vecteur de colonne), où les deux caractéristiques de l'échantillon x6 sont différentes des autres échantillons La différence de langue est relativement grande, par conséquent, x6 est considéré comme un échantillon de données singulier.

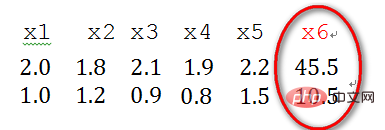
L'existence d'échantillons de données singuliers entraînera une augmentation du temps de formation et peut également conduire à un échec de convergence. Par conséquent, lorsqu'il existe des données d'échantillon singulières, les données prétraitées doivent être normalisées avant la formation  ; Versa, lorsqu'il n'y a pas de données d'échantillon singulières, la normalisation n'a pas besoin d'être effectuée.

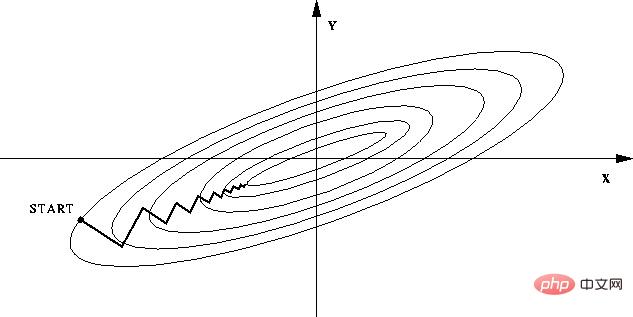
-- Si la normalisation n'est pas effectuée, la fonction objectif deviendra "plate" en raison de la grande différence entre les valeurs des différentes caractéristiques dans le vecteur de caractéristiques. De cette façon lors de la descente de pente, la direction de la pente s'écartera de la direction de la valeur minimale et fera de nombreux détours, c'est-à-dire que le temps d'entraînement sera trop long.

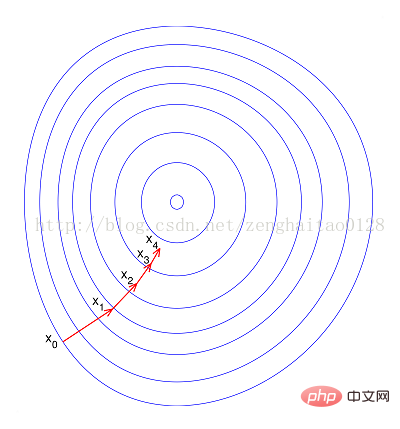
--Si elle est normalisée, la fonction objectif apparaîtra plus "ronde", ce qui accélérera considérablement l'entraînement et réduira le nombre de marches. De nombreux détours.

Pour résumer On voit que la normalisation présente les avantages suivants, à savoir

1) Vitesse après normalisation La vitesse de descente du gradient pour trouver la solution optimale ; >La normalisation a le potentiel d'améliorer la précision (comme KNN)

Remarque : Il n'existe aucune méthode de standardisation des données qui puisse améliorer la précision de l'algorithme et accélérer la vitesse de convergence de l'algorithme lorsqu'il est appliqué à chaque problème et chaque modèle.

Pour plus de connaissances connexes, veuillez visiter la colonne

FAQ !

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!