Résumé des questions courantes dans les entretiens Java (2)

1. Séquence de Fibonacci

[Sujet]

Tout le monde connaît la séquence de Fibonacci. On nous demande maintenant de saisir un nombre entier n. nième terme de la séquence de Fibonacci (en partant de 0, le 0ème terme est 0).

(Tutoriel vidéo recommandé : cours Java)

[Code]

package swear2offer.array;


public class FeiBoNaQi {

    /**
     * 大家都知道斐波那契数列，现在要求输入一个整数 n，
     * 请你输出斐波那契数列的第 n 项（从 0 开始，第 0 项为 0）。
     * 0,1,1,2,3,5
     * n<=39
     * */
    public int Fibonacci(int n) {
        if (n == 0) return 0;

        if (n == 1 || n== 2) return 1;

        return Fibonacci(n-1) + Fibonacci(n-2);
    }

    /**
     * 非递归方式，递归的数据结构使用的栈，那就是使用栈的方式
     * */
    public int NoRecursive(int n) {
        if (n>2) {
            int[] a = new int[n+1];
            a[0] = 0;
            a[1] = 1;
            a[2] = 1;

            for (int i=3; i<=n; i++) {
                a[i] = a[i-1] + a[i-2];
            }

            return a[n];
        } else {
            if (n == 0) return 0;
            else return 1;
        }
    }

    public static void main(String[] args) {
        System.out.println(new FeiBoNaQi().Fibonacci(39));
        System.out.println(new FeiBoNaQi().Fibonacci(39));
    }
}

2. Couverture rectangulaire

[Sujet]

On peut utiliser un petit rectangle de 21 pour recouvrir le plus grand rectangle horizontalement ou verticalement. Combien y a-t-il de façons de recouvrir un grand rectangle de taille 2*n avec n petits rectangles de taille 21 sans les chevaucher ?

Par exemple, lorsque n=3, il existe 3 méthodes de recouvrement pour un bloc rectangulaire de 2*3 :

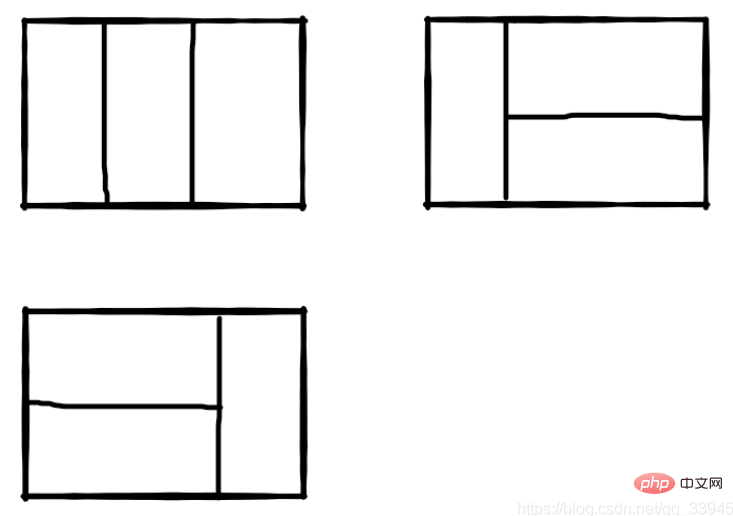
Code :

package swear2offer.array;

public class Rectangle {

    /**
     * f[0] = 0;
     * f[1] = 1;
     * f[2] = 2;
     * f[3] = 3;
     * f[4] = 5;
     * f[5] = 8;
     * f[n] = f[n-1] + f[n-2]
     * */

    public int RectCover(int target) {

        if (target < 4) return target;

        int[] f = new int[target + 1];
        int i;
        for (i=0; i<4; i++) f[i] = i;

        for (i=4; i<=target; i++) {
            f[i] = f[i-1] + f[i-2];
        }

        return f[target];
    }



    public static void main(String[] args) {
        System.out.println(new Rectangle().RectCover(5));
    }
}

[Réflexion 】

La façon la plus simple de résoudre le problème est de trouver les règles. À partir des règles résumées, nous pouvons voir que c'est la façon de réaliser la séquence de Fibonacci, l'autre est de résoudre le problème. selon le sens de la question et trouver la méthode de n , il est facile de penser à résoudre ce type de problème à partir de n-1, et le premier bloc est horizontal (f[n-2]) ou vertical (f[ n-1]), correspondant à différentes situations

(Recommandations pour des questions d'entretien plus connexes : questions et réponses d'entretien java)

3.

[Sujet]

Saisissez un entier et affichez le nombre de 1 dans la représentation binaire du nombre. Les nombres négatifs sont exprimés en complément à deux.

[Code]

package swear2offer.array;

public class Binary {

    /**
     * 输入一个整数，输出该数二进制表示中 1 的个数。其中负数用补码表示。
     * */
    public int NumberOf1(int n) {
        int count;
        count = 0;

        while(n != 0) {
            n = n & (n-1);// 与操作就是二进制的操作，适用原码和补码
            count ++;
        }

        return count;
    }
}

[Pensée]

Le complément à un d'un nombre négatif : Le bit de signe reste inchangé, et les bits restants sont inversés. nombre négatif : dans son complément à un Sur la base de +1

Si un entier n'est pas 0, alors au moins un bit de cet entier est 1. Si nous soustrayons 1 de cet entier, alors le 1 d'origine à l'extrême droite de l'entier deviendra 0, et tous les 0 après le 1 d'origine deviendront 1 (s'il y a des 0 après le 1 le plus à droite). Tous les bits restants ne seront pas affectés.

Par exemple : un nombre binaire 1100, le troisième chiffre en partant de la droite est le 1 le plus à droite. Après avoir soustrait 1, le troisième chiffre devient 0, les deux 0 suivants deviennent 1 et le premier 1 reste inchangé, le résultat est donc 1011. Nous constatons que le résultat de la soustraction de 1 est de changer le chiffre le plus à droite. Tous les bits commençant par 1 sont inversé. À ce stade, si nous effectuons l’opération ET entre l’entier d’origine et le résultat après soustraction de 1, tous les bits commençant par le 1 le plus à droite de l’entier d’origine deviendront 0. Par exemple, 1100&1011=1000. En d’autres termes, si vous soustrayez 1 d’un entier puis effectuez une opération ET avec l’entier d’origine, le 1 à l’extrême droite de l’entier sera transformé en 0. Il y aura alors autant de 1. comme il y en a dans le système binaire d'un entier.

4. Puissance entière d'une valeur

[Titre]

Étant donné une base numérique à virgule flottante de type double et un exposant entier de type int. Trouvez la base élevée à la puissance de l'exposant.
Assurez-vous que la base et l'exposant ne sont pas 0 en même temps

[Code]

package swear2offer.array;

public class Power {

    public double Power(double base, int exponent) {

        if (base == 0) return 0;
        if (exponent == 0) return 1;

        int count;
        boolean flag;
        double temp;

        count = 1;
        temp = base;
        flag = true;// 标记正负

        if (exponent < 0){
            exponent = -exponent;
            flag = false;
        }

        while (count < exponent) {
            base *= temp;
            count ++;
        }

        if (flag) {
            return base;
        } else {
            return 1/base;
        }

    }

    public static void main(String[] args) {
        System.out.println(new Power().Power(2,-3));
    }

}

[Réflexion]

Cette question n'est pas difficile et l'algorithme ne l'est pas très compliqué, mais le bord Il est facile de manquer des coins et des coins

Le premier point est le positif et le négatif de l'exposant Il est facile de manquer le nombre négatif

Deuxièmement, les cas. de base==0 et exponent==0 sont C'est différent

Enfin, lorsque la base est multipliée, vous ne pouvez pas l'utiliser elle-même, car la base grossit constamment.

5. Ajustez l'ordre du tableau pour que les nombres impairs soient devant les nombres pairs

[Titre]

Saisissez un tableau d'entiers et implémentez une fonction pour ajuster l'ordre des nombres dans le tableau de sorte que tous les nombres impairs soient situés dans la première moitié du tableau et que tous les nombres pairs soient situés dans la seconde moitié du tableau, garantissant que les positions relatives entre les nombres impairs et les nombres impairs, et les nombres pairs et pairs restent inchangés.

[Code]

package swear2offer.array;

import java.util.Arrays;

public class OddEven {

    /**
     * 输入一个整数数组，实现一个函数来调整该数组中数字的顺序，
     * 使得所有的奇数位于数组的前半部分，所有的偶数位于数组的后半部分，
     * 并保证奇数和奇数，偶数和偶数之间的相对位置不变。
     *
     * 时空复杂度较高的算法：
     * 新建一个数组b，用来保存奇数，在重新变量一次，保存偶数
     * 时空复杂度0(n)
     * */
    public void reOrderArray1(int [] array) {
        int n,i,j;
        n = array.length;

        int[] b = new int[n];

        j = 0;// 用来保存数组B的下标
        for (i=0; i<n; i++) {
            if (array[i]%2 != 0) {
                b[j] = array[i];
                j ++;
            }
        }
        for (i=0; i<n; i++) {
            if (array[i]%2 == 0){
                b[j] = array[i];
                j++;
            }
        }

        for (i=0; i<n; i++) {
            array[i] = b[i];
        }
    }

    /**
     * 采用的冒泡交换以及快速排序的思想：
     * 设定两个游标，游标分别用来标记奇数和偶数的下标，然后交换二者
     * 注意交换二者是无法保证顺序的，交换的ij之间还有进行平移。
     * */
    public void reOrderArray(int [] array) {

        int n,i,j,temp,p;

        n = array.length;
        i = 0;
        j = 0;
        while (i<n && j<n) {
            // i标记偶数下标
            while (i<n) {
                if (array[i]%2 ==0){
                    break;
                } else {
                    i++;
                }
            }
            j = i;
            // j标记奇数下标
            while (j<n) {
                if (array[j]%2 !=0){
                    break;
                } else {
                    j++;
                }
            }
            if (i<n && j<n) {
                // 此时ij已经在遇到的第一个偶数和奇数停下，把ij之间的内容平移
                temp = array[j];
                for (p=j; p>i; p--) {
                    array[p] = array[p-1];
                }
                array[i] = temp;
                // 此时把i,j标记到 未交换前的偶数位置的下一个
                i ++;
                j = i;
            }
        }
    }

    public static void main(String[] args) {
        int[] a = {1,4,6,3,2,5,8};
        int[] b = {2,4,6,1,3,5,7};
        new OddEven().reOrderArray(b);
        System.out.println(Arrays.toString(b));
    }
}

[Pensée]

Évidemment, la façon de créer un nouveau tableau est une manière délicate La question nécessite des opérations sur ce tableau, la seconde. La méthode consiste à opérer sur ce tableau, et cette méthode progressive à double curseur est très proche de l'idée du tri rapide.

Recommandations associées : Démarrez avec Java

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!