Maison >Problème commun >Traversée en profondeur d'abord et traversée en largeur d'abord
Traversée en profondeur d'abord et traversée en largeur d'abord
- (*-*)浩original
- 2019-12-19 09:29:0216139parcourir

Parcours en profondeur d'abord
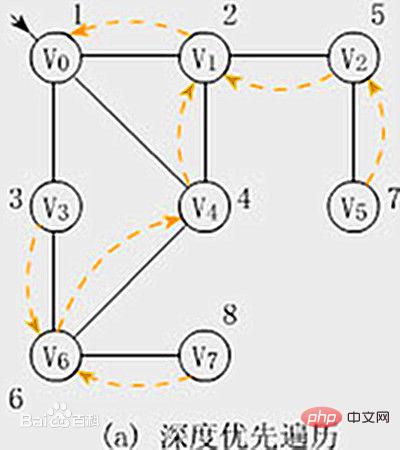
Supposons que l'état initial d'un graphe G donné est que tous les sommets n'ont pas été visités. Sélectionnez n'importe quel sommet v dans G comme point de départ initial (point source), puis le parcours en profondeur peut être défini comme suit : visitez d'abord le point de départ v et marquez-le comme visité, puis commencez à partir de v pour rechercher chaque point adjacent de ; v.w. (Apprentissage recommandé : Tutoriel vidéo Web front-end)
Si w n'a pas été visité auparavant, utilisez w comme nouveau point de départ pour continuer la traversée en profondeur d'abord jusqu'à ce que tous les chemins du graphique avoir des chemins vers le point source v Jusqu'à ce que tous les sommets connectés (également appelés sommets accessibles depuis le point source) aient été visités.
S'il y a encore des sommets non visités dans le graphique à ce moment-là, sélectionnez un autre sommet non visité comme nouveau point source et répétez le processus ci-dessus jusqu'à ce que tous les sommets du graphique aient été visités.
Le parcours en profondeur d'un graphique est similaire au parcours en pré-ordre d'un arbre. La caractéristique de la méthode de recherche adoptée est de rechercher d'abord dans le sens de la profondeur, autant que possible. Cette méthode de recherche est appelée recherche en profondeur. En conséquence, le parcours du graphique à l’aide de cette méthode est naturellement appelé parcours du graphique en profondeur.
Pour parler franchement, la traversée en profondeur est un algorithme qui ne heurte pas le mur. Il reviendra au nœud fourchu après avoir terminé un chemin et continuera la traversée.
Comme le montre la figure :
Traversée en largeur d'abord
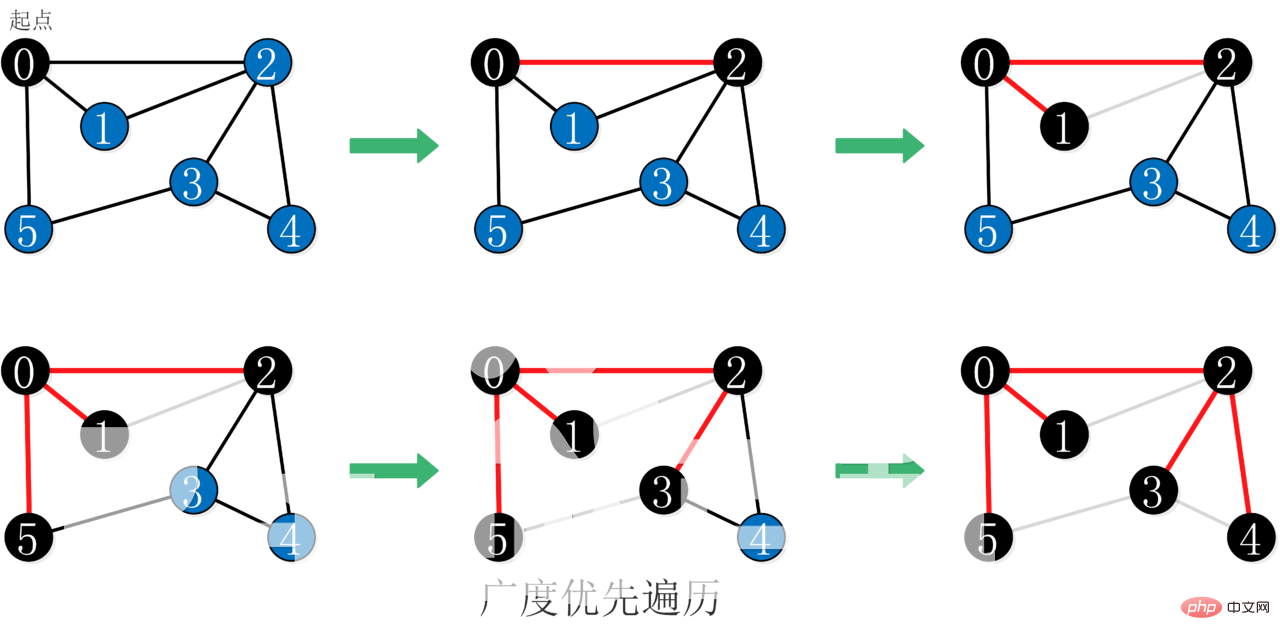
De quelque part dans la figure En partant du sommet V0, et en visitant ce sommet
En partant de V0, en visitant chaque point adjacent non visité W1, W2,...,Wk de V0 puis, en partant de W1, W2 ; ...,Wk, visitant chacun d'eux Points adjacents non visités
Répétez l'étape 2 jusqu'à ce que tous les sommets soient visités.
Il s'agit d'un algorithme couche par couche, similaire au parcours par ordre de couche d'un arbre.
Lors de la recherche en largeur, il sera parcouru à partir du point de départ dans une méthode d'expansion "couche par couche". Lors de l'expansion, chaque fois qu'un point est trouvé, il sera ajouté à la file d'attente jusqu'à la totalité. Le graphique a été parcouru.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

