complexité temporelle de la structure des données

Qu'est-ce que la complexité temporelle ?

Une certaine fonction dans l'algorithme est exécutée à plusieurs reprises n fois, représentée par T(n). Il existe maintenant une certaine fonction auxiliaire f(n), de sorte que lorsque n s'approche de l'infini, T La limite. la valeur de (n)/f(n) est une constante qui n'est pas égale à zéro, alors f(n) est dit être une fonction du même ordre de grandeur que T(n), enregistrée sous la forme T(n)= O(f(n)), et est appelé O (f(n)) est la complexité temporelle asymptotique de l'algorithme, appelée complexité temporelle.

Pour faire simple, ce qu'on appelle la complexité temporelle consiste à trouver une fonction f(n) du même type de courbe pour représenter la tendance de cet algorithme à mesure que n continue d'augmenter. Lorsque la quantité d'entrée n augmente progressivement, le cas limite de complexité temporelle est appelé « complexité temporelle asymptotique » de l'algorithme.

Méthode de calcul de la complexité temporelle :

1 Utilisez la constante 1 pour remplacer toutes les constantes additives dans le temps d'exécution

2. la fonction de temps d'exécution finale, seul le terme d'ordre le plus élevé

3 est conservé. Les coefficients du terme d'ordre le plus élevé

sont supprimés et classés par ordre de grandeur croissant des complexités temporelles courantes. sont :

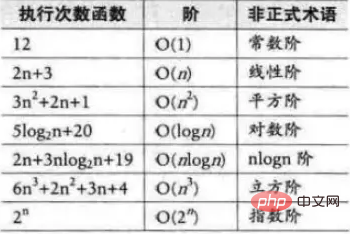
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!