Conversion de base en PHP

Système binaire

Quatre types

1. Système binaire : 0, 1, 2 à 1.

En golang, le binaire ne peut pas être utilisé directement pour représenter un entier, il suit les caractéristiques de c.

2. Décimal : 0-9, 10 à 1.
3. Octal : 0-7, chaque 8 vaut 1. Il commence par le chiffre 0.
4. Hexadécimal : 0-9 et A-F, complet 16 en 1. Cela commence par 0x ou 0X. A-F ici ne sont pas sensibles à la casse.

package main
import "fmt"
func main() {
    var i int = 5
    //二进制
    fmt.Printf("%b \n",i)

    var j int = 011 // 011=>8+1 = 9
    //八进制
    fmt.Println("j=",j)

    var k int = 0x11 //0x11 => 16+1 =17
    //十六进制 0x或者0X开头
    fmt.Println("k=",k)
}
//101
//j= 9
//k= 17

Icône de base

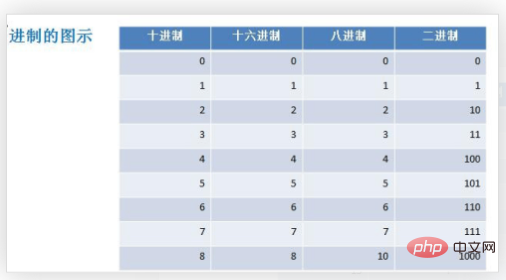
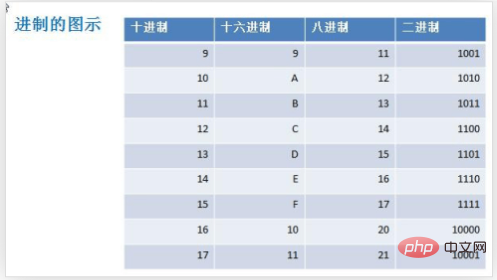
1. Convertir d'autres bases en décimal

1. Binaire à décimal
2. Octal à décimal
3. Hexadécimal à décimal

Binaire à décimal

Règle : du plus bas En commençant par le chiffre ( à droite), extrayez le nombre dans chaque chiffre, multipliez-le par 2 élevé à la puissance (ordre des chiffres - 1) et additionnez-le
Cas : 1011= 1 $2^3+02 ^2+12^1+12^0$=8+2+1 = 11

Octal à décimal

Règle : Commencez par le bit le plus bas ( A droite), extrayez le nombre dans chaque chiffre, multipliez-le par 8 élevé à la puissance (chiffre-1) et additionnez-le
Cas : 0123 = 1$8^2+28 ^1+3*8^0$=64+16+3 = 83

Hexadécimal en décimal

Règle : En partant du chiffre le plus bas (celui de droite), convertissez chaque chiffre Extrayez le nombre ci-dessus, multipliez-le par 16 élevé à la puissance (place-1) et additionnez-le
Cas : 0x34A = 10 $16^0+416^1+3*16^2 $ = 10+64+768 = 842

2. Convertir le décimal en d'autres bases

1. Convertir le décimal en binaire
2. Convertir le décimal en octal
3. Convertir le nombre décimal en hexadécimal

Décimal en binaire

Règle : Continuez à diviser le nombre par 2 jusqu'à ce que le quotient soit 0, puis inversez le reste obtenu à chaque étape, qui est le correspondant Binaire
cas : 56= 111000

Décimal vers octal

Règle : Continuez à diviser le nombre par 8 jusqu'à ce que le quotient soit 0, puis inversez le reste obtenu à chaque étape, ce qui est le
cas octal correspondant : 156=0234

Décimal en hexadécimal

Règle : Continuez à diviser le nombre par 16 jusqu'à ce que le quotient soit 0, puis convertissez chacun Le reste obtenu à cette étape est inversé, ce qui est le
cas hexadécimal correspondant : 356= 0x164

3 Binaire vers d'autres bases

1. Binaire vers octal
2. Binaire vers hexadécimal<.>

Binaire en octal

Règle : Combinez les nombres binaires en groupes de trois chiffres (en commençant par les chiffres bas -

côté droit !), convertissez-les en nombre octal correspondantCas : 11010101 = 11/010/101 = 324 = 0324

Binaire en hexadécimal

Règle : Convertir binaire Les nombres sont par groupes de quatre chiffres (combiner à partir de les chiffres bas--

côté droit!), et convertissez-les en nombres hexadécimaux correspondantsCas : 11010101= 1101/0101 = 13/5 = D5 = 0xD5

4. Octal et hexadécimal en binaire

Octal en binaire
1. Hexadécimal en binaire

Conversion octal en binaire

Règle : Combiner chaque chiffre du nombre octal (en commençant par le bit le plus bas)--

droit  ! ), convertissez-le en un nombre binaire à 3 chiffres correspondantCas : 0237= 10/011/111 = 10011111

Hexadécimal en binaire

Règle : Convertir dix Chaque chiffre de l'hexadécimal le nombre (combiné à partir du bit faible -

côté droit!) peut être converti en un nombre binaire correspondant à 4 chiffresCas : 0x237= 10/0011/0111 = 1000110111

C'est un peu brouillon, résumons-le à nouveau

---

Résumé du système de base

1 : Type : 2 , 8, 10, 16

2 : Composition spécifique

1. 2:0, 1
2. 8:0-7
3. 10:0-9
4. 16:0-9, A, B, C, D , E, F

3 : Convertir les autres bases en décimal

multiplié par (numéro de bit -1) fois de la base convertie Puis somme up

4 : Convertir le nombre décimal vers d'autres bases

Diviser le nombre converti par le nombre à convertir jusqu'à ce que le quotient soit 0, puis le reste obtenu à chaque étape est inversé

5 : Binaire vers d'autres bases

vers octal, en commençant par la droite, divisez tous les trois chiffres

Convertir en hexadécimal, commencer par la droite, diviser tous les quatre chiffres

6 :

Convertir l'octal, l'hexadécimal en binaire

Convertir l'octal, commencer par la droite, divisé en chaque trois chiffres

Conversion hexadécimale, en partant de la droite, divisée en quatre chiffres

Pour plus d'articles techniques liés à PHP, veuillez visiter l'étude de la colonne

Tutoriel PHP !

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!