Python peut-il résoudre des équations aux dérivées partielles ?

fipy

La loi de Fick fait référence à la relation entre le flux de transfert de masse et le gradient de concentration dans le processus de diffusion moléculaire lorsque des phénomènes de transfert de masse se produisent sans s'appuyer sur la loi de mélange macroscopique. La loi de Fick a été proposée par Adolf Fick en 1855.

L'équation aux dérivées partielles de la diffusion dynamique peut être obtenue à partir de la deuxième loi de Fick. La résolution peut obtenir la distribution de concentration et la courbe de sortie.

Je ne sais pas s'il existe une solution analytique à ce problème, mais la solution numérique est une solution plus générale.

fipy est un package python de solution PDE rare qui est toujours vivant. L'auteur a adapté ce programme sur la base de l'exemple officiel.

Recommandations associées : "Tutoriel vidéo Python"

Question

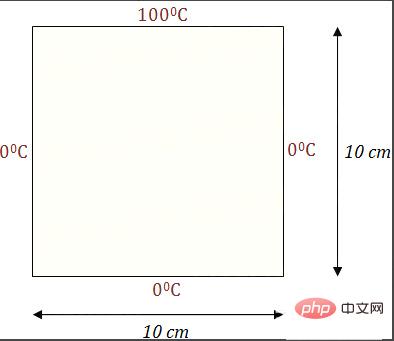
Une plaque plate bidimensionnelle avec un sommet de 1 degré Celsius (100 degrés Celsius) D'accord, juste un coefficient), les trois autres bords sont à 0 degré Celsius et la planche entière est à 0 degré Celsius au moment initial. Au fil du temps, la chaleur est transférée sur la planche, et finalement. atteint un état d'équilibre. Nous voulons non seulement connaître la répartition de la température de l'état d'équilibre, mais également savoir comment la température évolue au fil du temps. Le transfert de chaleur est donné par une équation différentielle, qui peut être simplement comprise comme la chaleur est transférée dans la direction dans laquelle la température diminue le plus rapidement.

Le côté droit de la formule est le gradient de température, et le côté gauche est le changement de température avec le temps

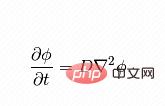
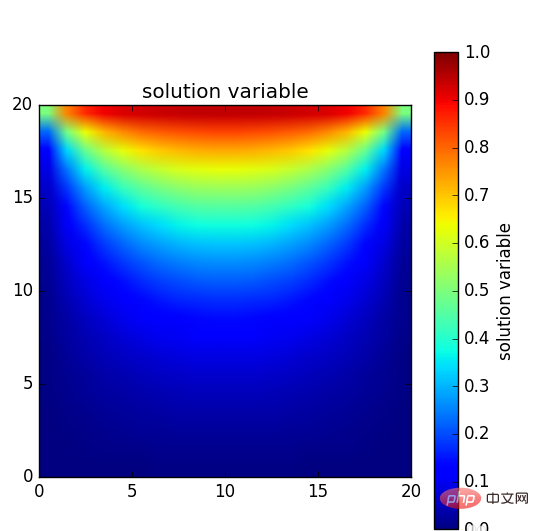
La répartition finale de la température de l'ensemble de la carte. Elle montre grossièrement comment

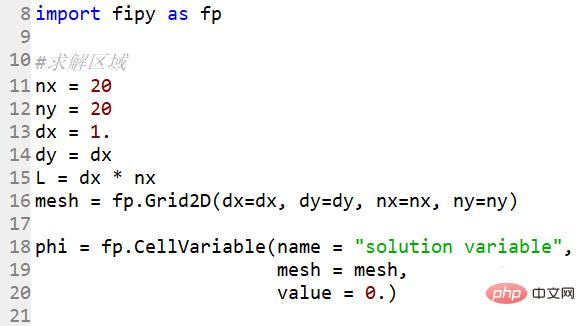
Un seul paquet doit être importé

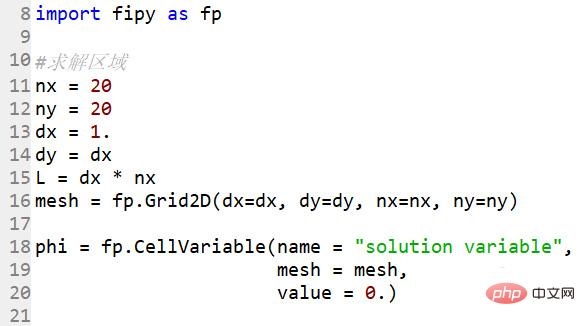
import fipy as fp

Déterminez la zone de solution, un point de grille 20*20

#Zone de solution nx = 20ny = 20dx = 1.dy = dxL = dx * nxmesh = fp.Grid2D(dx=dx, dy=dy, nx=nx, ny=ny)

pHI = fp.cellvariable (nom = "SOLUTION VARIABLE", Mesh = Mesh, Value = 0.)

Créer une équation de division différentielle

Établir les conditions aux limites

Créer un dessin

Résoudre

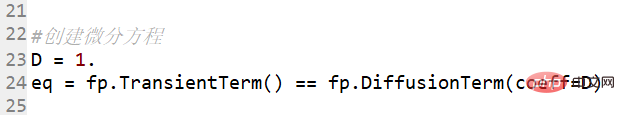
Il est recommandé pour l'exécuter dans la ligne de commande, où vous pouvez obtenir des images animées, ipython Il n'y a que la dernière image dedans

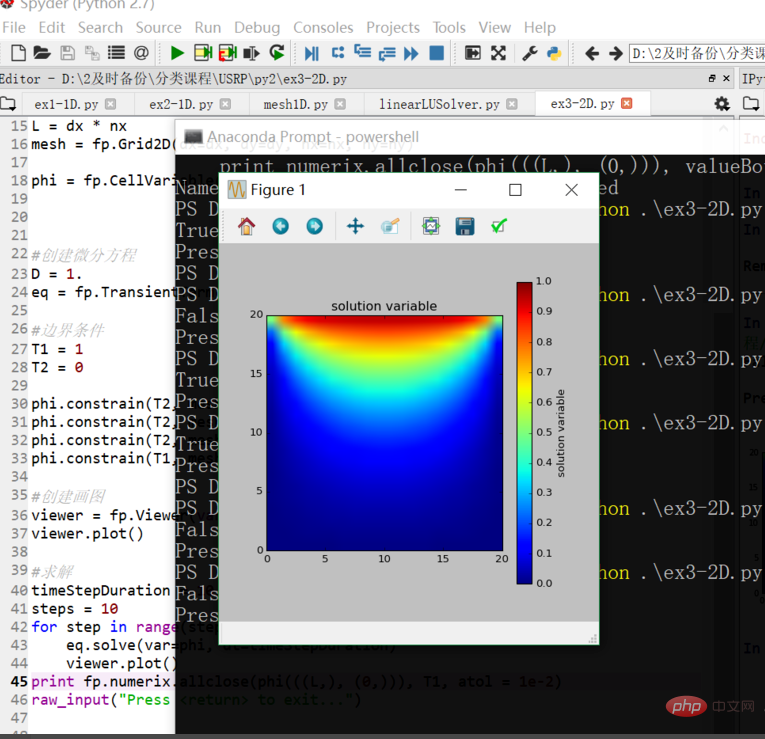Il n'y a que la dernière image dans l'ipython de Spyder

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!