Comment comprendre les structures de données et les algorithmes (Python)

Compréhension des structures de données et des algorithmes en Python : les structures de données en Python font référence à la description statique de la relation entre les éléments de données, et les algorithmes font référence à des méthodes ou des étapes pour résoudre des problèmes. Conçue, la structure des données est porteuse du problème que l'algorithme doit traiter.

La structure des données et l'algorithme sont des compétences de base essentielles pour un développeur de programme, nous devons donc prendre l'initiative de les apprendre et de les accumuler. Ensuite, je vais vous présenter ces deux points de connaissances en détail dans cet article. j'espère que cela vous sera utile.

[Cours recommandés : Tutoriel Python]

Présentation du concept

Regardons d'abord une question :

Si a+b+c=1000 et a2+b2=c^2 (a , b, c sont des nombres naturels), comment trouver toutes les combinaisons possibles de a, b, c ?

Premier essai

import time
start_time = time.time()
# 注意是三重循环
for a in range(0, 1001):    
for b in range(0, 1001):        
for c in range(0, 1001):            
if a**2 + b**2 == c**2 and a+b+c == 1000:
print("a, b, c: %d, %d, %d" % (a, b, c))
end_time = time.time()
print("elapsed: %f" % (end_time - start_time))
print("complete!")

Résultats d'exécution :

a, b, c: 0, 500, 500
a, b, c: 200, 375, 425
a, b, c: 375, 200, 425
a, b, c: 500, 0, 500
elapsed: 1066.117884
complete!

Le temps d'exécution peut atteindre 17,8 minutes

Proposition d'algorithme

Concept d'algorithme

L'algorithme est l'essence même du traitement informatique de l'information, car un programme informatique est essentiellement un algorithme qui indique à l'ordinateur les étapes exactes pour effectuer une tâche spécifiée. Généralement, lorsqu'un algorithme traite des informations, il lira les données d'un périphérique d'entrée ou d'une adresse de stockage des données, et écrira les résultats sur un périphérique de sortie ou une adresse de stockage pour un rappel ultérieur.
Les algorithmes sont des méthodes et des idées indépendantes pour résoudre des problèmes.
Pour les algorithmes, le langage d'implémentation n'a pas d'importance, ce qui est important c'est l'idée.
L'algorithme peut avoir différentes versions de description et d'implémentation de langage (telles que la description C, la description C++, la description Python, etc.). Nous utilisons maintenant le langage Python pour le décrire et l'implémenter.

Cinq caractéristiques des algorithmes

Entrée : L'algorithme a 0 ou plusieurs entrées

Sortie : L'algorithme a au moins 1 ou plusieurs sorties

Finitude : l'algorithme se terminera automatiquement après un nombre limité d'étapes sans boucler à l'infini, et chaque étape peut être complétée dans un délai acceptable

Déterministe : chaque étape de l'algorithme Toutes ont des significations définies et là il n'y aura aucune ambiguïté

Faisabilité : Chaque étape de l'algorithme est réalisable, ce qui signifie que chaque étape peut être exécutée un nombre limité de fois

Deuxième tentative

import time
start_time = time.time()
# 注意是两重循环
for a in range(0, 1001):    
for b in range(0, 1001-a):
c = 1000 - a - b        
if a**2 + b**2 == c**2:            
print("a, b, c: %d, %d, %d" % (a, b, c))
end_time = time.time()print("elapsed: %f" % (end_time - start_time))print("complete!")

Résultats d'exécution :

a, b, c: 0, 500, 500
a, b, c: 200, 375, 425
a, b, c: 375, 200, 425
a, b, c: 500, 0, 500
elapsed: 0.632128

Notez que le temps d'exécution est de 0,632128 secondes

Mesure de l'efficacité de l'algorithme

Efficacité de l'algorithme de réaction du temps d'exécution

Pour le même problème, nous donnons deux algorithmes de résolution. Dans la mise en œuvre des deux algorithmes, nous comparons le temps d'exécution du programme. Après calcul, nous avons constaté que le temps d'exécution du programme. deux programmes sont très différents. De là, nous pouvons tirer une conclusion : le temps d'exécution du programme algorithmique peut refléter l'efficacité de l'algorithme, c'est-à-dire la qualité de l'algorithme.

La valeur temps seule est-elle absolument fiable ?

Et si nous exécutions notre deuxième tentative d'algorithme sur un ordinateur avec une configuration ancienne et peu performante ? Très probablement, le temps d'exécution ne sera pas beaucoup plus rapide que l'exécution de l'algorithme 1 sur notre ordinateur.

Il n'est pas forcément objectif et précis de comparer les avantages et les inconvénients d'algorithmes basés uniquement sur le temps d'exécution !

L'exécution d'un programme ne peut être séparée de l'environnement informatique (y compris le matériel et le système d'exploitation). Ces raisons objectives affecteront la vitesse du programme et se refléteront dans le temps d'exécution du programme. Alors comment juger objectivement la qualité d’un algorithme ?

Complexité temporelle et "notation Big O"

Nous supposons que le temps nécessaire à l'ordinateur pour effectuer chaque opération de base de l'algorithme est une unité de temps fixe, donc combien d'opérations de base représentent le nombre d'unités de temps que cela prendra. Étant donné que l'unité de temps exacte est différente selon les environnements de la machine, mais que le nombre d'opérations de base effectuées par l'algorithme (c'est-à-dire le nombre d'unités de temps qu'il prend) est le même dans l'ordre de grandeur, l'influence de l'environnement de la machine peut donc être ignoré et objectif L'efficacité temporelle de l'algorithme de réaction.

Pour l'efficacité temporelle de l'algorithme, nous pouvons utiliser la "notation Big O" pour l'exprimer.

"Notation Big O" : Pour une fonction entière monotone f, s'il existe une fonction entière g et une constante réelle c>0, telle que pour un n suffisamment grand il y a toujours f(n)< =c* g(n), on dit que la fonction g est une fonction asymptotique de f (en ignorant la constante), enregistrée sous la forme f(n)=O(g(n)). C'est-à-dire que dans le sens limite de tendre vers l'infini, le taux de croissance de la fonction f est contraint par la fonction g, c'est-à-dire que les caractéristiques de la fonction f et de la fonction g sont similaires.

Complexité temporelle : Supposons qu'il existe une fonction g telle que le temps nécessaire à l'algorithme A pour traiter un exemple de problème de taille n soit T(n)=O(g(n)), alors elle est appelée O(g(n)) est la complexité temporelle asymptotique de l'algorithme A, appelée complexité temporelle, notée T(n)

Comment comprendre la « notation Big O »

对于算法进行特别具体的细致分析虽然很好，但在实践中的实际价值有限。对于算法的时间性质和空间性质，最重要的是其数量级和趋势，这些是分析算法效率的主要部分。而计量算法基本操作数量的规模函数中那些常量因子可以忽略不计。例如，可以认为3n2和100n2属于同一个量级，如果两个算法处理同样规模实例的代价分别为这两个函数，就认为它们的效率“差不多”，都为n2级。

最坏时间复杂度

分析算法时，存在几种可能的考虑：

算法完成工作最少需要多少基本操作，即最优时间复杂度

算法完成工作最多需要多少基本操作，即最坏时间复杂度

算法完成工作平均需要多少基本操作，即平均时间复杂度
对于最优时间复杂度，其价值不大，因为它没有提供什么有用信息，其反映的只是最乐观最理想的情况，没有参考价值。

对于最坏时间复杂度，提供了一种保证，表明算法在此种程度的基本操作中一定能完成工作。

对于平均时间复杂度，是对算法的一个全面评价，因此它完整全面的反映了这个算法的性质。但另一方面，这种衡量并没有保证，不是每个计算都能在这个基本操作内完成。而且，对于平均情况的计算，也会因为应用算法的实例分布可能并不均匀而难以计算。

因此，我们主要关注算法的最坏情况，亦即最坏时间复杂度。

时间复杂度的几条基本计算规则

基本操作，即只有常数项，认为其时间复杂度为O(1)

顺序结构，时间复杂度按加法进行计算

循环结构，时间复杂度按乘法进行计算

分支结构，时间复杂度取最大值

判断一个算法的效率时，往往只需要关注操作数量的最高次项，其它次要项和常数项可以忽略

在没有特殊说明时，我们所分析的算法的时间复杂度都是指最坏时间复杂度

算法分析

第一次尝试的算法核心部分

or a in range(0, 1001):    
for b in range(0, 1001):        
for c in range(0, 1001):            
if a**2 + b**2 == c**2 and a+b+c == 1000:
print("a, b, c: %d, %d, %d" % (a, b, c))

时间复杂度：

T(n) = O(n * n * n) = O(n³)

第二次尝试的算法核心部分

for a in range(0, 1001):    
for b in range(0, 1001-a):
c = 1000 - a - b        
if a**2 + b**2 == c**2:            
print("a, b, c: %d, %d, %d" % (a, b, c))

时间复杂度：

T(n) = O(n * n * (1+1)) = O(n * n) = O(n²)

由此可见，我们尝试的第二种算法要比第一种算法的时间复杂度好多的。

常见时间复杂度

执行次数函数举例	阶	非正式术语
12	O(1)	常数阶
2n + 3	O(n)	线性阶
3n² +2n + 1	O(n²)	平方阶
5log2n+20	O(logn)	对数阶
2n+3nlog2n+19	O(nlogn)	nlogn阶
6n³ +2n² +3n +  1	O(n³)	立方阶
2n	O(2n)	指数阶

注意，经常将log2n（以2为底的对数）简写成logn

常见时间复杂度之间的关系

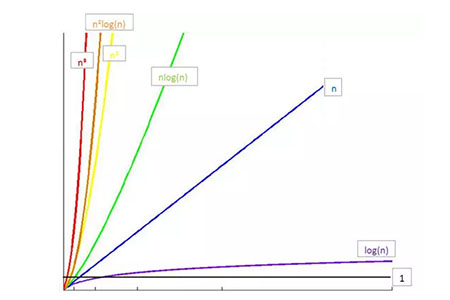
所消耗的时间从小到大

O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) < O(nn)

Python内置类型性能分析

timeit模块

timeit模块可以用来测试一小段Python代码的执行速度。

class timeit.Timer(stmt=&#39;pass&#39;, setup=&#39;pass&#39;, timer=<timer function>)

Timer是测量小段代码执行速度的类。

stmt参数是要测试的代码语句（statment）

setup参数是运行代码时需要的设置

timer参数是一个定时器函数，与平台有关。

timeit.Timer.timeit(number=1000000)

Timer类中测试语句执行速度的对象方法。number参数是测试代码时的测试次数，默认为1000000次。方法返回执行代码的平均耗时，一个float类型的秒数。

list的操作测试

def test1():
   l = []   for i in range(1000):
      l = l + [i]def test2():
   l = []   for i in range(1000):
      l.append(i)def test3():
   l = [i for i in range(1000)]def test4():
   l = list(range(1000))from timeit import Timer
t1 = Timer("test1()", "from __main__ import test1")
print("concat ",t1.timeit(number=1000), "seconds")
t2 = Timer("test2()", "from __main__ import test2")
print("append ",t2.timeit(number=1000), "seconds")
t3 = Timer("test3()", "from __main__ import test3")
print("comprehension ",t3.timeit(number=1000), "seconds")
t4 = Timer("test4()", "from __main__ import test4")
print("list range ",t4.timeit(number=1000), "seconds")
# ('concat ', 1.7890608310699463, 'seconds')
# ('append ', 0.13796091079711914, 'seconds')
# ('comprehension ', 0.05671119689941406, 'seconds')
# ('list range ', 0.014147043228149414, 'seconds')

pop操作测试

x = range(2000000)
pop_zero = Timer("x.pop(0)","from __main__ import x")
print("pop_zero ",pop_zero.timeit(number=1000), "seconds")
x = range(2000000)
pop_end = Timer("x.pop()","from __main__ import x")
print("pop_end ",pop_end.timeit(number=1000), "seconds")
# ('pop_zero ', 1.9101738929748535, 'seconds')
# ('pop_end ', 0.00023603439331054688, 'seconds')

测试pop操作：从结果可以看出，pop最后一个元素的效率远远高于pop第一个元素

可以自行尝试下list的append(value)和insert(0,value),即一个后面插入和一个前面插入？？？

list内置操作的时间复杂度

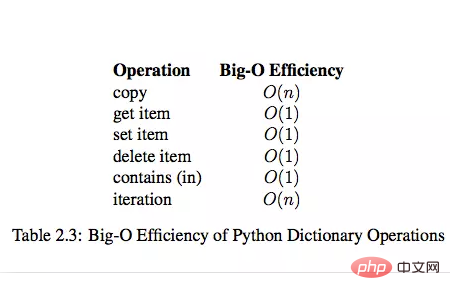
dict内置操作的时间复杂度

数据结构

概念

数据是一个抽象的概念，将其进行分类后得到程序设计语言中的基本类型。如：int，float，char等。数据元素之间不是独立的，存在特定的关系，这些关系便是结构。数据结构指数据对象中数据元素之间的关系。

Python给我们提供了很多现成的数据结构类型，这些系统自己定义好的，不需要我们自己去定义的数据结构叫做Python的内置数据结构，比如列表、元组、字典。而有些数据组织方式，Python系统里面没有直接定义，需要我们自己去定义实现这些数据的组织方式，这些数据组织方式称之为Python的扩展数据结构，比如栈，队列等。

算法与数据结构的区别

数据结构只是静态的描述了数据元素之间的关系。

高效的程序需要在数据结构的基础上设计和选择算法。

程序 = 数据结构 + 算法

总结：算法是为了解决实际问题而设计的，数据结构是算法需要处理的问题载体

抽象数据类型(Abstract Data Type)

抽象数据类型(ADT)的含义是指一个数学模型以及定义在此数学模型上的一组操作。即把数据类型和数据类型上的运算捆在一起，进行封装。引入抽象数据类型的目的是把数据类型的表示和数据类型上运算的实现与这些数据类型和运算在程序中的引用隔开，使它们相互独立。

最常用的数据运算有五种

插入

删除

修改

查找

排序

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!