Méthode de base pour implémenter la recherche binaire en Java (avec code)

Ce que cet article vous apporte concerne la méthode de base d'implémentation de la recherche binaire en Java (avec du code). Il a une certaine valeur de référence. Les amis dans le besoin peuvent s'y référer.

La recherche binaire est particulièrement facile à comprendre. Elle est similaire à l'idée de diviser pour régner utilisée dans le tri rapide et la fusion. À chaque fois, le nombre du milieu est comparé au nombre cible, puis il est déterminé. qu'il soit plus grand ou plus petit, et l'intervalle est réduit de moitié.

Par exemple :

Xiao Hong a sélectionné un nombre entre 1 et 100 (ce nombre est 56) et a demandé à Xiao Ming de deviner, ce qui a donné le dialogue suivant :

Xiao Ming Première supposition : 68

Xiao Hong : Grand

Deuxième supposition de Xiao Ming : 35

Xiao Hong : Petit

Troisième supposition de Xiao Ming Première supposition : 58

Xiaohong : Trop grand

Quatrième supposition de Xiao Ming : 49

Xiaohong : Petit

Cinquième supposition de Xiao Ming :54

Xiaohong : Trop petit

Sixième supposition de Xiao Ming : 56

Xiaohong : bingo ! ! !

Nous pouvons voir que dans la conversation ci-dessus, Xiao Ming peut réduire l'intervalle à chaque fois qu'il devine jusqu'à ce que la réponse soit correcte

La recherche binaire est comme ceci. Par exemple, nous avons maintenant les tableaux 8. , 11, 19 , 23, 27, 33, 45, 55, 67, 98, utilisez la recherche binaire comme indiqué ci-dessous :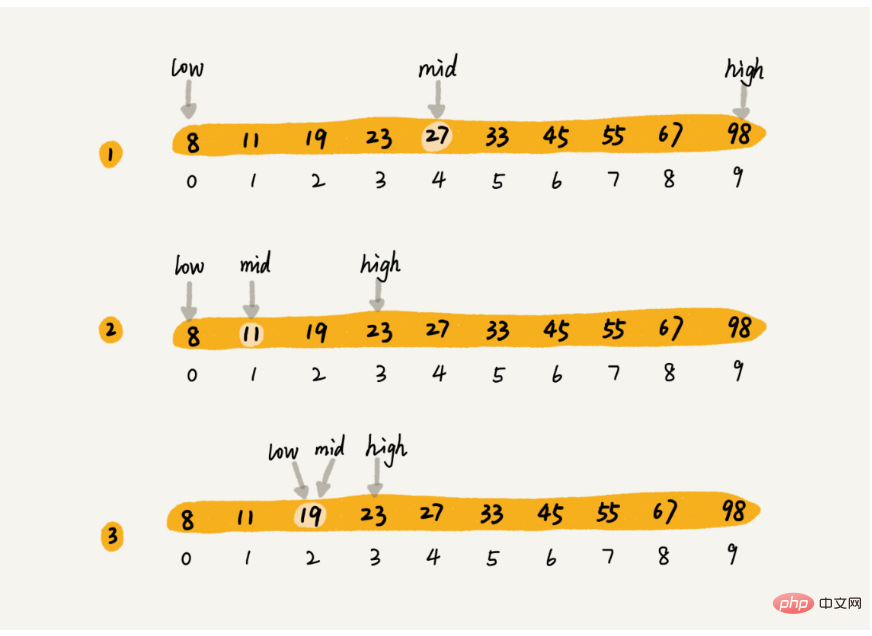

Chaque fois que vous pouvez réduire l'intervalle de moitié, nous pouvons voir que le l'intervalle change comme suit :

Lorsque la taille de l'intervalle est infiniment proche de 1, k = log2n, donc la complexité temporelle est O(logn).

Est-ce très facile à comprendre ? Voici une recherche binaire simple que j'ai implémentée en Java (remarque : c'est l'implémentation la plus simple, les variantes de la recherche binaire sont très compliquées et je ne la maîtrise pas encore)

package com.structure.search;

/**
 * 二分查找法
 *
 * @author zhangxingrui
 * @create 2019-02-15 21:29
 **/
public class BinarySearch {

    public static void main(String[] args) {
        int[] nums = new int[]{4, 6, 9, 19, 30, 40, 500, 3450, 50004, 4334343};
        System.out.println(binarySearch(nums, 0, nums.length - 1, 30));
        System.out.println(binarySearch(nums, 50004));
    }

    /**
     * @Author: xingrui
     * @Description: 二分查找法（针对有序数组且不存在重复元素-递归方式实现）
     * @Date: 21:37 2019/2/15
     */
    private static int binarySearch(int[] nums, int p, int r, int k){
        if(p > r)
            return -1;

        int mid = (p + r) / 2;
        if(nums[mid] == k)
            return mid;

        if(k > nums[mid])
            return binarySearch(nums, mid + 1, r, k);
        else
            return binarySearch(nums, p,  mid - 1, k);
    }

    /**
     * @Author: xingrui
     * @Description: 二分查找法（针对有序数组且不存在重复元素-循环实现）
     * @Date: 21:37 2019/2/15
     */
    private static int binarySearch(int[] nums, int k){
        int p = 0;
        int r = nums.length - 1;
        while (p <= r){
            int mid = (p + r) / 2;

            if(nums[mid] == k)
                return mid;

            if(k > nums[p])
                p = mid + 1;
            else
                r = mid - 1;
        }
        return -1;
    }

}

Le code est très simple, et il faut prêter attention à la condition aux limites p<=r.

Il ressort également du code que l'implémentation simple a de grandes limites et ne peut être appliquée qu'à des tableaux ordonnés sans données en double.

Et la recherche binaire ne convient pas aux requêtes de données à petite échelle (car les requêtes de données à petite échelle ne sont pas nécessaires), c'est facile à comprendre en même temps, elle ne convient pas aux données à grande échelle ; question, pourquoi est-ce du drap de laine ?

C'est à cause de ce qui précède : la recherche binaire convient aux données sous-jacentes à l'aide de tableaux, mais le tableau est un espace mémoire continu. Lorsque les données sont volumineuses, si vous souhaitez utiliser la recherche binaire, alors le sous-jacent. implémentation des données Just

ne peut utiliser que des tableaux, ce qui n'est pas très bon. En supposant que mes données ont un G, je dois alors demander un espace mémoire continu de 1 G. Oh mon dieu, j'ai peur d'être rassasié.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!