Analyse algorithmique de la pile et de la file d'attente en JavaScript

Le contenu de cet article concerne l'analyse algorithmique des piles et des files d'attente en JavaScript. Il a une certaine valeur de référence. Les amis dans le besoin peuvent s'y référer.

1. Comprendre la structure des données

Qu'est-ce que la structure des données ? Ce qui suit est une explication tirée de Wikipédia

La structure des données est la façon dont un ordinateur stocke et organise les données

La structure des données signifie interface ou encapsulation : une structure de données peut être considérée comme une interface entre deux fonctions, ou est représentée par un fichier de données. type La méthode d'encapsulation du contenu stocké composé d'unions

Nous utilisons des structures de données dans le codage quotidien, car les tableaux sont les structures de données en mémoire les plus simples

• <.>Tableau

• Pile

• File d'attente

• Liste chaînée

• Arbre

• Graphique

• Tas

• Hash

Apprenons-en davantage sur les piles et les files d'attente..

2. Pile

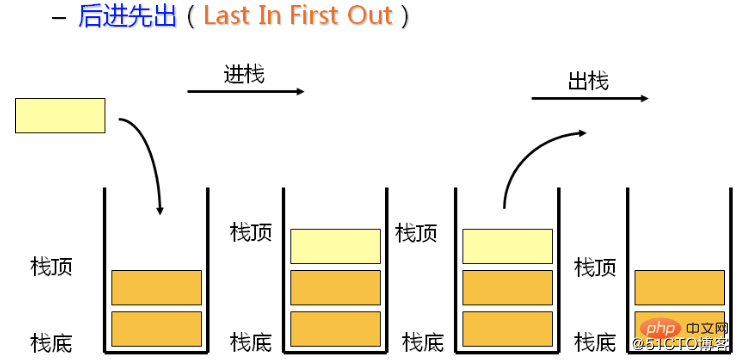
2.1 Structure des données de la pileLa. stack est une collection ordonnée qui suit le principe du dernier entré, premier sorti (LIFO). Les éléments nouvellement ajoutés ou à supprimer sont stockés à la même extrémité de la pile, appelée haut de la pile, et l'autre extrémité est appelée bas de la pile. Dans la pile, les nouveaux éléments se trouvent en haut de la pile et les anciens éléments en bas.

Analogie avec les objets de la vie : une pile de livres ou d'assiettes rapprochées

2.2 Mise en œuvre de la pile

Ce qui suit les méthodes sont couramment utilisées dans les piles ordinaires :

push ajoute un (ou plusieurs) nouveaux éléments en haut de la pile

pop déborde de l'élément supérieur de la pile et renvoie l'élément supprimé

peek renvoie l'élément supérieur de la pile sans modifier la pile

isEmpty renvoie vrai s'il n'y a aucun élément dans la pile, sinon renvoie faux

size renvoie le nombre d'éléments dans la pile

clear efface la pile

class Stack {
  constructor() {
    this._items = []; // 储存数据
  }
  // 向栈内压入一个元素
  push(item) {
    this._items.push(item);
  }
  // 把栈顶元素弹出
  pop() {
    return this._items.pop();
  }
  // 返回栈顶元素
  peek() {
    return this._items[this._items.length - 1];
  }
  // 判断栈是否为空
  isEmpty() {
    return !this._items.length;
  }
  // 栈元素个数
  size() {
    return this._items.length;
  }
  // 清空栈
  clear() {
    this._items = [];
  }
}

Regardons maintenant en arrière et réfléchissons à ce qu'est la pile dans la structure de données.

Tout à coup, j'ai découvert que ce n'était pas si magique, c'était juste une encapsulation des données originales. Le résultat de l'encapsulation est :

ne se soucie pas des éléments qu'il contient, mais n'exploite que l'élément supérieur de la pile Dans ce cas, le codage sera plus contrôlable.

2.3 Application de la pile

(1) Décimal à base arbitraire

Exigences : Étant donné une fonction, saisir la valeur cible et base, affiche le numéro de base correspondant (hexadécimal maximum)

baseConverter(10, 2) ==> 1010
baseConverter(30, 16) ==> 1E

Analyse : L'essence de la conversion de base : divisez la valeur cible une à la fois Base, la valeur arrondie obtenue est la nouvelle valeur cible, enregistrez le reste jusqu'à ce que la valeur cible soit inférieure à 0, et enfin combinez les restes dans l'ordre inverse. Utilisez la pile pour enregistrer le reste et poussez-le dans la pile, puis retirez-le lors de la combinaison

// 进制转换
function baseConverter(delNumber, base) {
  const stack = new Stack();
  let rem = null;
  let ret = [];
  // 十六进制中需要依次对应A~F
  const digits = '0123456789ABCDEF';

  while (delNumber > 0) {
    rem = Math.floor(delNumber % base);
    stack.push(rem);
    delNumber = Math.floor(delNumber / base);
  }

  while (!stack.isEmpty()) {
    ret.push(digits[stack.pop()]);
  }

  return ret.join('');
}

console.log(baseConverter(100345, 2)); //输出11000011111111001
console.log(baseConverter(100345, 8)); //输出303771
console.log(baseConverter(100345, 16)); //输出187F9

(2) Calcul de l'expression polonaise inversée

Exigences : Les expressions polonaises inverses, également appelées expressions postfixes, convertissent des expressions complexes en expressions qui peuvent s'appuyer sur des opérations simples pour obtenir des résultats de calcul, telles que converti en (a+b)*(c+d)a b + c d + *

["4", "13", "5", "/", "+"] ==> (4 + (13 / 5)) = 6
["10", "6", "9", "3", "+", "-11", "*", "/", "*", "17", "+", "5", "+"]
==> ((10 * (6 / ((9 + 3) * -11))) + 17) + 5

Analyse : utilise le symbole comme nœud déclencheur. Une fois qu'un symbole est rencontré, les deux premiers éléments du symbole sont exploités en fonction du symbole et le nouveau résultat est poussé dans la pile jusqu'à ce qu'il n'y ait qu'un seul élément. dans la pile

function isOperator(str) {
  return ['+', '-', '*', '/'].includes(str);
}
// 逆波兰表达式计算
function clacExp(exp) {
  const stack = new Stack();
  for (let i = 0; i <p>(3) Utiliser une pile normale pour implémenter une pile avec la méthode <strong> <code>min</code></strong></p><p> Idée : <strong> Utiliser deux piles pour stocker les données, dont l'une est nommée </strong>, spécifiquement utilisée pour stocker les données, et l'autre nommée <code>dataStack</code>, spécifiquement utilisée pour stocker les plus petites données de la pile. Gardez toujours le même nombre d'éléments dans les deux piles. Lorsque vous poussez la pile, comparez la taille de l'élément poussé avec l'élément <code>minStack</code> supérieur de la pile, s'il est plus petit que l'élément supérieur de la pile, poussez-le. directement sur la pile. Sinon, copiez l'élément supérieur de la pile et poussez-le sur la pile. Lorsque vous faites apparaître le haut de la pile, faites simplement apparaître les deux. De cette façon, l'élément supérieur de la pile de <code>minStack</code> est toujours la valeur minimale. <code>minStack</code></p><pre class="brush:php;toolbar:false">class MinStack {
  constructor() {
    this._dataStack = new Stack();
    this._minStack = new Stack();
  }

  push(item) {
    this._dataStack.push(item);
    // 为空或入栈元素小于栈顶元素，直接压入该元素
    if (this._minStack.isEmpty() || this._minStack.peek() > item) {
      this._minStack.push(item);
    } else {
      this._minStack.push(this._minStack.peek());
    }
  }

  pop() {
    this._dataStack.pop();
    return this._minStack.pop();
  }

  min() {
    return this._minStack.peek();
  }
}

const minstack = new MinStack();

minstack.push(3);
minstack.push(4);
minstack.push(8);
console.log(minstack.min()); // 3
minstack.push(2);
console.log(minstack.min()); // 2

3. File d'attente

3.1 Structure des données de la file d'attenteLa file d'attente suit le premier entré, premier sorti (FIFO , également connu sous le nom de premier entré, premier sorti) Un ensemble ordonné d'articles basé sur le principe (premier arrivé, premier servi). La file d'attente ajoute de nouveaux éléments à la queue et supprime des éléments du haut. Le dernier élément ajouté doit être mis en file d'attente en fin de file d'attente

Analogie : File d'attente des achats dans la vie quotidienne

3.2 Mise en œuvre de la file d'attente

Les méthodes suivantes sont couramment utilisées dans les files d'attente ordinaires :

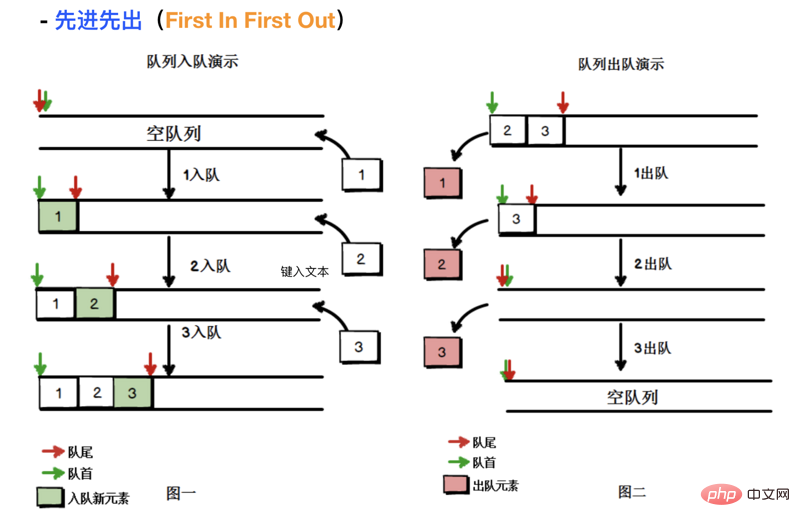
• Ajouter un (ou plusieurs) nouveaux éléments à la fin de la file d'attente enqueue

• Supprimez le premier élément de la file d'attente (c'est-à-dire le début de la file d'attente) et renvoyez l'élément supprimé dequeue

• Renvoyez le premier élément de l'élément de file d'attente, la file d'attente n'apporte aucune modification head

• Renvoie le dernier élément de la file d'attente, la file d'attente n'apporte aucune modificationtail

• isEmpty 队列内无元素返回true，否则返回false

• size 返回队列内元素个数

• clear 清空队列

class Queue {
  constructor() {
    this._items = [];
  }

  enqueue(item) {
    this._items.push(item);
  }

  dequeue() {
    return this._items.shift();
  }

  head() {
    return this._items[0];
  }

  tail() {
    return this._items[this._items.length - 1];
  }

  isEmpty() {
    return !this._items.length;
  }

  size() {
    return this._items.length;
  }

  clear() {
    this._items = [];
  }
}

与栈类比，栈仅能操作其头部，队列则首尾均能操作，但仅能在头部出尾部进。当然，也印证了上面的话：栈和队列并不关心其内部元素细节，也无法直接操作非首尾元素。

3.3 队列的应用

（1）约瑟夫环（普通模式）

要求: 有一个数组a[100]存放0~99；要求每隔两个数删掉一个数，到末尾时循环至开头继续进行，求最后一个被删掉的数。

分析: 按数组创建队列，依次判断元素是否满足为指定位置的数，如果不是则enqueue到尾部，否则忽略，当仅有一个元素时便输出

// 创建一个长度为100的数组
const arr_100 = Array.from({ length: 100 }, (_, i) => i*i);

function delRing(list) {
  const queue = new Queue();
  list.forEach(e => { queue.enqueue(e); });
  
  let index = 0;
  while (queue.size() !== 1) {
    const item = queue.dequeue();
    index += 1;
    if (index % 3 !== 0) {
      queue.enqueue(item);
    }
  }

  return queue.tail();
}

console.log(delRing(arr_100)); // 8100 此时index=297

（2）菲波那切数列（普通模式）

要求: 使用队列计算斐波那契数列的第n项
分析: 斐波那契数列的前两项固定为1，后面的项为前两项之和，依次向后，这便是斐波那契数列。

function fibonacci(n) {
    const queue = new Queue();
    queue.enqueue(1);
    queue.enqueue(1);
    
    let index = 0;
    while(index <p><strong>（3）用队列实现一个栈</strong></p><p><strong>要求:</strong> 用两个队列实现一个栈<br><strong>分析:</strong> 使用队列实现栈最主要的是在队列中找到栈顶元素并对其操作。具体的思路如下：</p><ol class=" list-paddingleft-2">
<li><p>两个队列，一个备份队列<code>emptyQueue</code>，一个是数据队列<code>dataQueue</code>；</p></li>
<li><p>在确认栈顶时，依次<code>dequeue</code>至备份队列，置换备份队列和数据队列的引用即可</p></li>
</ol><pre class="brush:php;toolbar:false">class QueueStack {
  constructor() {
    this.queue_1 = new Queue();
    this.queue_2 = new Queue();
    this._dataQueue = null; // 放数据的队列
    this._emptyQueue = null; // 空队列,备份使用
  }

  // 确认哪个队列放数据,哪个队列做备份空队列
  _initQueue() {
    if (this.queue_1.isEmpty() && this.queue_2.isEmpty()) {
      this._dataQueue = this.queue_1;
      this._emptyQueue = this.queue_2;
    } else if (this.queue_1.isEmpty()) {
      this._dataQueue = this.queue_2;
      this._emptyQueue = this.queue_1;
    } else {
      this._dataQueue = this.queue_1;
      this._emptyQueue = this.queue_2;
    }
  };

  push(item) {
    this.init_queue();
    this._dataQueue.enqueue(item);
  };

  peek() {
    this.init_queue();
    return this._dataQueue.tail();
  }

  pop() {
    this.init_queue();
    while (this._dataQueue.size() > 1) {
      this._emptyQueue.enqueue(this._dataQueue.dequeue());
    }
    return this._dataQueue.dequeue();
  };
};

学习了栈和队列这类简单的数据结构，我们会发现。数据结构并没有之前想象中那么神秘，它们只是规定了这类数据结构的操作方式：栈只能对栈顶进行操作，队列只能在尾部添加在头部弹出；且它们不关心内部的元素状态。

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!