Maison >développement back-end >Tutoriel Python >Le principe et l'implémentation de l'algorithme K-plus proche voisin en python (code source ci-joint)
Le principe et l'implémentation de l'algorithme K-plus proche voisin en python (code source ci-joint)
- 不言avant
- 2018-10-27 14:21:554239parcourir
Ce que cet article vous apporte concerne le principe et la mise en œuvre de l'algorithme du K-plus proche voisin en python (code source ci-joint). Il a une certaine valeur de référence. Les amis dans le besoin peuvent s'y référer. pour vous.
L'algorithme du k-voisin le plus proche effectue une classification en mesurant la distance entre les différentes valeurs de caractéristiques.
Principe de l'algorithme du k-plus proche voisin
Pour un ensemble d'échantillons d'entraînement avec des étiquettes, après la saisie de nouvelles données sans étiquettes, chaque fonctionnalité des nouvelles données est intégrée au échantillon Les caractéristiques correspondant aux données sont comparées, et les k données les plus similaires dans l'ensemble de données échantillon sont sélectionnées selon l'algorithme, et la classification avec le plus d'occurrences parmi les k données les plus similaires est sélectionnée comme classification du nouveau données.
Implémentation de l'algorithme du k-voisin le plus proche
Voici seulement la prédiction d'une seule nouvelle donnée, et la prédiction de plusieurs nouvelles données en même temps est placée plus tard .
Supposons qu'il existe un ensemble d'échantillons de formation X_train (X_train.shape=(10, 2)), la marque correspondante y_train (y_train.shape=(10,), incluant 0, 1), utilisez matplotlib. pyplot à dessiner Il est représenté comme suit (les points verts représentent la marque 0, les points rouges représentent la marque 1) :
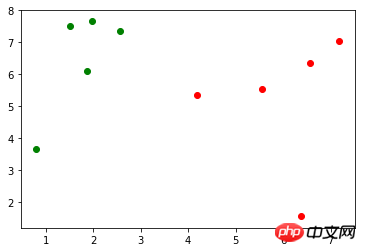
Il y a une nouvelle donnée : x (x = np.array([3.18557125, 6.03119673])), la représentation du dessin est la suivante (points bleus) :
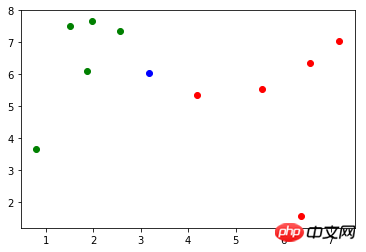
Tout d'abord, utilisez Distance d'Euler La formule calcule la distance de x à chaque échantillon en Toute influence :
import math distances = [math.sqrt(np.sum((x_train - x) ** 2)) for x_train in X_train]
Troisièmement, prenez les marques correspondant aux k échantillons les plus proches : np.argsort()
import numpy as np nearest = np.argsort(distances)Enfin, comptez les marques correspondant aux k échantillons les plus proches, trouvez la classification prédite avec la plus grande proportion de marques, qui est x La classification prédite dans cet exemple est 0 :
topK_y = [y_train[i] for i in nearest[:k]]Encapsulez le code ci-dessus dans une méthode : <.>
from collections import Counter votes = Counter(topK_y) votes.most_common(1)[0][0]L'algorithme du k-voisin le plus proche dans Scikit Learn
import numpy as np import math from collections import Counter def kNN(k, X_train, y_train, x): distances = [math.sqrt(np.sum((x_train - x) ** 2)) for x_train in X_train] nearest = np.argsort(distances) topK_y = [y_train[i] for i in nearest[:k]] votes = Counter(topK_y) return votes.most_common(1)[0][0]Un processus typique d'algorithme d'apprentissage automatique consiste à entraîner (ajuster) l'ensemble de données d'entraînement via l'algorithme d'apprentissage automatique pour produire un modèle et utiliser ce modèle pour prédire les résultats de l'exemple d'échantillon d'entrée.
Pour l'algorithme du k-voisin le plus proche, il s'agit d'un algorithme spécial sans modèle, mais nous considérons son ensemble de données d'entraînement comme un modèle . C'est ainsi que cela est géré dans Scikit Learn. 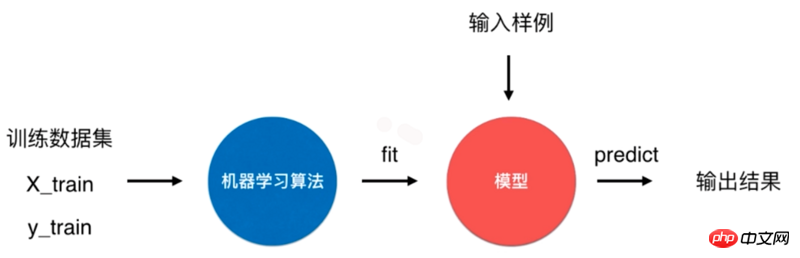 L'algorithme du k-voisin le plus proche dans Scikit Learn utilise
L'algorithme du k-voisin le plus proche dans Scikit Learn utilise
"entraîne" le classificateur en fonction de l'ensemble de données d'entraînement, cette méthode renvoie le classificateur lui-même :
from sklearn.neighbors import KNeighborsClassifier kNN_classifier = KNeighborsClassifier(n_neighbors=6)La méthode
prédit l'entrée. Par conséquent, la méthode nécessite que le paramètre transmis soit de type matrice. Par conséquent, l'opération fit() est d'abord effectuée sur x :
kNN_classifier.fit(X_train, y_train)
La valeur y_predict est 0, ce qui est cohérent avec le résultat de la méthode kNN implémentée précédemment. predict()reshape
X_predict = x.reshape(1, -1) y_predict = kNN_classifier.predict(X_predict)Définissez une classe KNNClassifier Sa méthode constructeur passe le paramètre k, qui représente les données les plus similaires sélectionnées lors de la prédiction Number. :
La méthode entraîne le classificateur et renvoie le classificateur lui-même :
class KNNClassifier: def __init__(self, k): self.k = k self._X_train = None self._y_train = None
La méthode prédit l'ensemble de données à tester, et le paramètre X_predict le type est une matrice. Cette méthode utilise la compréhension de liste pour parcourir X_predict et appelle la méthode fit() une fois pour chaque donnée à tester.
def fit(self, X_train, y_train): self._X_train = X_train self._y_train = y_train return self
predict()Précision de l'algorithme_predict()
def predict(self, X_predict): y_predict = [self._predict(x) for x in X_predict] return np.array(y_predict) def _predict(self, x): distances = [math.sqrt(np.sum((x_train - x) ** 2)) for x_train in self._X_train] nearest = np.argsort(distances) topK_y = [self._y_train[i] for i in nearest[:self.k]] votes = Counter(topK_y) return votes.most_common(1)[0][0]
Problèmes avec le modèle
Le modèle est entraîné via l'échantillon d'entraînement défini ci-dessus. Mais nous ne savons pas à quel point ce modèle est bon, et il reste encore deux problèmes.Si le modèle est mauvais, les résultats prédits ne sont pas ceux que nous souhaitons. En même temps, dans des situations réelles, il est difficile d’obtenir le véritable label et de tester le modèle.
- Lors de l'entraînement du modèle, les échantillons d'entraînement ne contiennent pas tous les marqueurs.
- Pour la première question, une certaine proportion (telle que 20 %) des données de l'ensemble d'échantillons est généralement utilisée comme données de test, et les données restantes sont utilisées comme données d'entraînement. Prenons comme exemple les données d'iris fournies dans Scikit Learn, qui contiennent 150 échantillons.
Divisez maintenant l'échantillon en 20 % de données de test d'échantillon et 80 % de données d'entraînement en proportion :
Utilisez X_train et y_train comme données d'entraînement pour entraîner le modèle, X_test et y_test Utilisé comme données de test pour vérifier l'exactitude du modèle.import numpy as np from sklearn import datasets iris = datasets.load_iris() X = iris.data y = iris.target
Pour la deuxième question, prenons comme exemple les données d'iris fournies dans Scikit Learn. Le contenu de la marque y est :
.array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
发现0、1、2是以顺序存储的,在将样本划分为训练数据和测试数据过程中,如果训练数据中才对标记只包含0、1,这样的训练数据对于模型的训练将是致命的。以此,应将样本数据先进行随机处理。
np.random.permutation() 方法传入一个整数 n,会返回一个区间在 [0, n) 且随机排序的一维数组。将 X 的长度作为参数传入,返回 X 索引的随机数组:
shuffle_indexes = np.random.permutation(len(X))
将随机化的索引数组分为训练数据的索引与测试数据的索引两部分:
test_ratio = 0.2 test_size = int(len(X) * test_ratio) test_indexes = shuffle_indexes[:test_size] train_indexes = shuffle_indexes[test_size:]
再通过两部分的索引将样本数据分为训练数据和测试数据:
X_train = X[train_indexes] y_train = y[train_indexes] X_test = X[test_indexes] y_test = y[test_indexes]
可以将两个问题的解决方案封装到一个方法中,seed 表示随机数种子,作用在 np.random 中:
import numpy as np def train_test_split(X, y, test_ratio=0.2, seed=None): if seed: np.random.seed(seed) shuffle_indexes = np.random.permutation(len(X)) test_size = int(len(X) * test_ratio) test_indexes = shuffle_indexes[:test_size] train_indexes = shuffle_indexes[test_size:] X_train = X[train_indexes] y_train = y[train_indexes] X_test = X[test_indexes] y_test = y[test_indexes] return X_train, X_test, y_train, y_test
Scikit Learn 中封装了 train_test_split() 方法,放在了 model_selection 模块中:
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
算法正确率
通过 train_test_split() 方法对样本数据进行了预处理后,开始训练模型,并且对测试数据进行验证:
from sklearn.neighbors import KNeighborsClassifier kNN_classifier = KNeighborsClassifier(n_neighbors=6) kNN_classifier.fit(X_train, y_train) y_predict = kNN_classifier.predict(X_test)
y_predict 是对测试数据 X_test 的预测结果,其中与 y_test 相等的个数除以 y_test 的个数就是该模型的正确率,将其和 y_test 进行比较可以算出模型的正确率:
def accuracy_score(y_true, y_predict): return sum(y_predict == y_true) / len(y_true)
调用该方法,返回一个小于等于1的浮点数:
accuracy_score(y_test, y_predict)
同样在 Scikit Learn 的 metrics 模块中封装了 accuracy_score() 方法:
from sklearn.metrics import accuracy_score accuracy_score(y_test, y_predict)
Scikit Learn 中的 KNeighborsClassifier 类的父类 ClassifierMixin 中有一个 score() 方法,里面就调用了 accuracy_score() 方法,将测试数据 X_test 和 y_test 作为参数传入该方法中,可以直接计算出算法正确率。
class ClassifierMixin(object): def score(self, X, y, sample_weight=None): from .metrics import accuracy_score return accuracy_score(y, self.predict(X), sample_weight=sample_weight)
超参数
前文中提到的 k 是一种超参数,超参数是在算法运行前需要决定的参数。 Scikit Learn 中 k-近邻算法包含了许多超参数,在初始化构造函数中都有指定:
def __init__(self, n_neighbors=5, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=None, **kwargs): # code here
这些超参数的含义在源代码和官方文档[scikit-learn.org]中都有说明。
算法优缺点
k-近邻算法是一个比较简单的算法,有其优点但也有缺点。
优点是思想简单,但效果强大, 天然的适合多分类问题。
缺点是效率低下,比如一个训练集有 m 个样本,n 个特征,则预测一个新的数据的算法复杂度为 O(m*n);同时该算法可能产生维数灾难,当维数很大时,两个点之间的距离可能也很大,如 (0,0,0,...,0) 和 (1,1,1,...,1)(10000维)之间的距离为100。
源码地址
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

