Maison >interface Web >js tutoriel >JavaScript calcule la distance entre deux lieux par latitude et longitude
JavaScript calcule la distance entre deux lieux par latitude et longitude
- 不言original
- 2018-09-10 14:40:538323parcourir
Comment calculer la distance entre deux lieux avec JavaScript ? Je pense qu'il existe de nombreuses façons d'y parvenir. L'article suivant vous présentera JavaScript pour calculer la distance entre deux lieux en fonction de la longitude et de la latitude.
Récemment, en raison de besoins professionnels, j'ai recherché en ligne des méthodes pour calculer la distance entre deux endroits en fonction de la longitude et de la latitude. J'ai découvert qu'il s'agissait soit d'une méthode géométrique, de dessiner une image, de faire un dessin. un tas de lignes auxiliaires, puis prouver le raisonnement, ou simplement l'appliquer sans rien dire de formule. Cet article présente une manière facile à comprendre de trouver cette distance.
Idée
La terre est un ellipsoïde irrégulier. Pour plus de simplicité, nous la traitons comme une sphère pour le calcul.
La distance la plus courte entre deux endroits sur une sphère est la longueur de l'arc mineur d'un grand cercle passant par deux points.
L'idée est la suivante :
Longueur de l'arc ← Longueur de la corde (distance entre deux points) ← Coordonnées à deux points (Coordonnées rectangulaires) ← Latitude et longitude
Calculer
1. Conversion de coordonnées
Supposons :
Le rayon de la terre est $R$
La ligne reliant le centre de la terre à E 0° N 0° est l'axe des x
La ligne reliant le centre de la terre à E 90° N 0° est l'axe des y
La ligne reliant le centre de la terre la terre à E 0° N 90° est l'axe z
Il y a un point $A sur la surface de la terre $, la longitude est $e$, la latitude est $n$, et l'unité est des radians
alors les coordonnées de $A$ peuvent être exprimées comme :
$$ x = R cdot cos(n) cdot cos(e)\ y = R cdot cos(n) cdot sin(e)\ z = R cdot sin(n) $$
Code
const R = 6371
const {cos, sin, PI} = Math
let getPoint = (e, n) => {
//首先将角度转为弧度
e *= PI/180
n *= PI/180
reutrn {
x: R*cos(n)*cos(e),
y: R*cos(n)*sin(e),
z: R*sin(n)
}
}
2 Calculer la distance entre deux points en fonction des coordonnées
C'est trop simple, sautez
.3. Trouvez la longueur de l'arc en fonction de la longueur de la corde
Vous pouvez faire un dessin pour aider à comprendre :
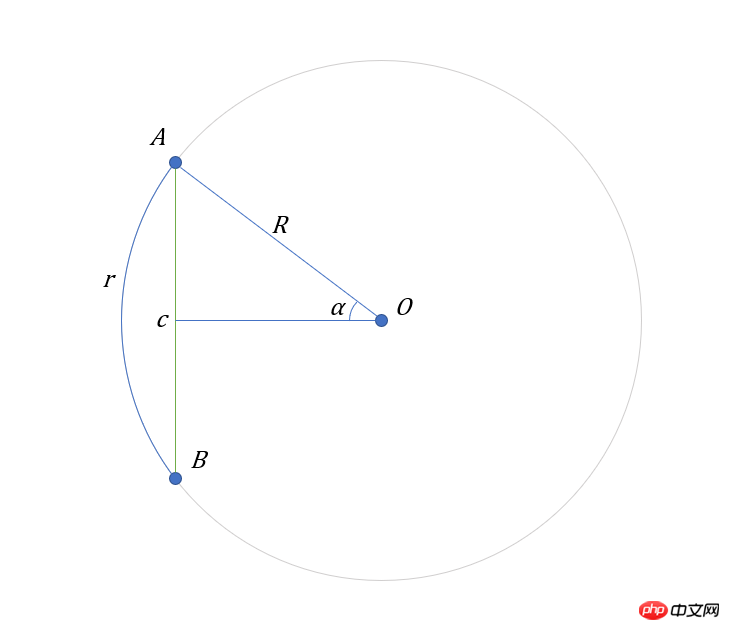
Maintenant la longueur de la corde est connue $ c$, le rayon $R$, nécessite la longueur de l'arc $r$
C'est très simple, il suffit de trouver d'abord la taille de $∠alpha$ :
$$ alpha = arcsin(c/2/R)\ r = 2alpha cdot R $$
Code
const {asin} = Math
const R = 6371
r = asin(c/2/R)*2*R
Code final
/**
* 获取两经纬度之间的距离
* @param {number} e1 点1的东经, 单位:角度, 如果是西经则为负
* @param {number} n1 点1的北纬, 单位:角度, 如果是南纬则为负
* @param {number} e2
* @param {number} n2
*/
function getDistance(e1, n1, e2, n2){
const R = 6371
const { sin, cos, asin, PI, hypot } = Math
/** 根据经纬度获取点的坐标 */
let getPoint = (e, n) => {
e *= PI/180
n *= PI/180
//这里 R* 被去掉, 相当于先求单位圆上两点的距, 最后会再将这个距离放大 R 倍
return {x: cos(n)*cos(e), y: cos(n)*sin(e), z: sin(n)}
}
let a = getPoint(e1, n1)
let b = getPoint(e2, n2)
let c = hypot(a.x - b.x, a.y - b.y, a.z - b.z)
let r = asin(c/2)*2*R
return r
}
Recommandations associées :
Calculer la distance entre deux lieux en fonction de la longitude et latitude
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

