js_Trois algorithmes pour la traversée d'un arbre binaire avant, au milieu et en arrière_implémentation d'un arbre binaire simple

À propos de l'établissement et du parcours des arbres binaires, cet article fournit une introduction détaillée, ainsi que les algorithmes de parcours d'arbres binaires de pré-ordre, de parcours d'arbres binaires dans l'ordre et de parcours d'arbres binaires de post-ordre. également cité dans le but de permettre à chacun d'y voir plus clairement. L'introduction de cet article doit commencer par les arbres binaires et les arbres de recherche binaires pour une compréhension facile. apache php mysql

Arbre binaire et arbre de recherche binaire

Termes associés à l'arbre :

Nœud : chaque élément de l'arbre appelé un nœud,

nœud racine : un nœud situé au sommet de l'arbre entier, il n'a pas de nœud parent, comme le montre la figure 5 ci-dessus

nœud enfant : descendants d'autres nœuds

nœud feuilles : les éléments sans nœuds enfants sont appelés nœuds feuilles, comme le montre la figure 3 8 24

Arbre binaire : l'arbre binaire est une structure de données et sa relation organisationnelle est comme un arbre dans la nature. La définition dans la langue officielle est la suivante : il s'agit d'un ensemble d'éléments finis, soit vide, soit constitué d'un élément appelé racine et de deux arbres binaires disjoints, appelés respectivement sous-arbre gauche et sous-arbre droit.

Arbre de recherche binaire :
L'arbre de recherche binaire est également appelé arbre de recherche binaire (BST). Il nous permet uniquement de stocker une valeur plus petite dans le nœud gauche que le nœud parent, et une valeur plus petite dans le nœud parent. nœud droit que le nœud parent. Pour des valeurs plus grandes, l'image ci-dessus montre un arbre de recherche binaire.

Implémentation du code

Créez d'abord une classe pour représenter un arbre de recherche binaire. Il devrait y avoir une classe Node à l'intérieur pour créer des nœuds

    function BinarySearchTree () {
        var Node = function(key) {
            this.key = key,
            this.left = null,
            this.right = null
        }
        var root = null
    }

Il devrait également y en avoir. quelques méthodes :

• insert(key) Insérer une nouvelle clé

• inOrderTraverse() Effectuer un parcours dans l'ordre de l'arbre et imprimer les résultats

• preOrderTraverse() effectue un parcours pré-commandé de l'arbre et imprime les résultats

• postOrderTraverse() effectue un parcours post-ordre de l'arbre et imprime les résultats

• search(key) recherche la clé dans l'arborescence, si elle existe elle renvoie vrai, si elle n'existe pas elle renvoie fasle

• findMin() renvoie la clé dans l'arborescence Valeur minimale

• findMax() Renvoie la valeur maximale dans l'arborescence

• remove(key) Supprimer une clé dans l'arborescence

Insérer une clé dans l'arborescence

Insérer une nouvelle clé dans l'arborescence La page d'accueil doit créer une instance de classe Node. pour représenter le nouveau nœud, vous devez donc créer une nouvelle classe Node et la fusionner. Transmettez la valeur clé qui doit être insérée, et elle s'initialisera automatiquement sur un nouveau nœud avec des nœuds gauche et droit nuls

Ensuite, vous devez faire quelques jugements. Tout d'abord, déterminez si l'arbre est vide. S'il est vide, le nœud nouvellement inséré sera le nœud racine. S'il n'est pas vide, appelez une méthode auxiliaire insertNode() et passez-la. le nœud racine et le nouveau nœud dans

    this.insert = function(key) {
        var newNode = new Node(key)
        if(root === null) {
            root = newNode
        } else {
            insertNode(root, newNode)
        }
    }

Définissez la méthode insertNode(), cette méthode s'appellera récursivement, pour trouver la position appropriée du nœud nouvellement ajouté

    var insertNode = function(node, newNode) {
        if (newNode.key <= node.key) {
            if (node.left === null) {
                node.left = newNode
            }else {
                insertNode(node.left, newNode)
            }
        }else {
            if (node.right === null) {
                node.right = newNode
            }else {
                insertNode(node.right, newNode)
            }
        }
    }

Complétez la méthode de parcours dans l'ordre

Pour implémenter le parcours dans l'ordre, nous avons besoin d'une méthode inOrderTraverseNode(node), qui peut s'appeler récursivement Traverser chaque nœud

    this.inOrderTraverse = function() {
        inOrderTraverseNode(root)
    }

Cette méthode imprimera la valeur clé de chaque nœud. Cela nécessite une condition de terminaison récursive - vérifiez si le nœud entrant est nul, sinon continuez. S'appeler récursivement pour vérifier les nœuds gauche et droit du nœud
est également très simple à mettre en œuvre :

    var inOrderTraverseNode = function(node) {
        if (node !== null) {
            inOrderTraverseNode(node.left)
            console.log(node.key)
            inOrderTraverseNode(node.right)
        }
    }

Parcours de précommande, parcours de post-commande

Avec la méthode de parcours dans l'ordre, uniquement Avec de légers changements, vous pouvez implémenter le parcours de pré-commande et le parcours de post-commande
Le code ci-dessus :

De cette façon, vous pouvez effectuer un parcours dans l'ordre de l'ensemble de l'arbre

    // 实现先序遍历
    this.preOrderTraverse = function() {
        preOrderTraverseNode(root)
    }
    var preOrderTraverseNode = function(node) {
        if (node !== null) {
            console.log(node.key)
            preOrderTraverseNode(node.left)
            preOrderTraverseNode(node.right)
        }
    }

    // 实现后序遍历
    this.postOrderTraverse = function() {
        postOrderTraverseNode(root)
    }
    var postOrderTraverseNode = function(node) {
        if (node !== null) {
            postOrderTraverseNode(node.left)
            postOrderTraverseNode(node.right)
            console.log(node.key)
        }
    }

Découvrir Eh bien, en fait, les instructions internes ont changé de recto et de verso positions, qui est simplement conforme aux trois règles de parcours : parcours en pré-ordre (racine-gauche-droite), parcours en ordre (racine-gauche-droite) et parcours en ordre (gauche-droite) <.>

Faisons d'abord un test

Le code complet est maintenant le suivant :

    function BinarySearchTree () {
        var Node = function(key) {
            this.key = key,
            this.left = null,
            this.right = null
        }
        var root = null
        
        //插入节点
        this.insert = function(key) {
            var newNode = new Node(key)
            if(root === null) {
                root = newNode
            } else {
                insertNode(root, newNode)
            }
        }
        var insertNode = function(node, newNode) {
            if (newNode.key <= node.key) {
                if (node.left === null) {
                    node.left = newNode
                }else {
                    insertNode(node.left, newNode)
                }
            }else {
                if (node.right === null) {
                    node.right = newNode
                }else {
                    insertNode(node.right, newNode)
                }
            }
        } 
        
        //实现中序遍历
        this.inOrderTraverse = function() {
            inOrderTraverseNode(root)
        }
        var inOrderTraverseNode = function(node) {
            if (node !== null) {
                inOrderTraverseNode(node.left)
                console.log(node.key)
                inOrderTraverseNode(node.right)
            }
        }
        // 实现先序遍历
        this.preOrderTraverse = function() {
            preOrderTraverseNode(root)
        }
        var preOrderTraverseNode = function(node) {
            if (node !== null) {
                console.log(node.key)
                preOrderTraverseNode(node.left)
                preOrderTraverseNode(node.right)
            }
        }

        // 实现后序遍历
        this.postOrderTraverse = function() {
            postOrderTraverseNode(root)
        }
        var postOrderTraverseNode = function(node) {
            if (node !== null) {
                postOrderTraverseNode(node.left)
                postOrderTraverseNode(node.right)
                console.log(node.key)
            }
        }
    }

Il a en fait terminé la méthode d'ajout de nouveaux nœuds et de parcours, testons-le :

Définissons un tableau contenant quelques éléments

var arr = [9,6,3,8,12,15]

Nous insérons chaque élément de arr dans l'arbre de recherche binaire en conséquence, puis imprimons le résultat

    var tree = new BinarySearchTree()
    arr.map(item => {
        tree.insert(item)
    })
    tree.inOrderTraverse()
    tree.preOrderTraverse()
    tree.postOrderTraverse()

Après avoir exécuté le code, regardons d'abord la situation de l'arbre entier après avoir inséré le nœud :

Résultat de sortie

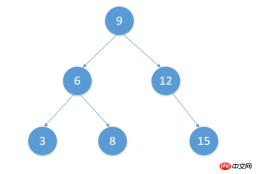
En séquence Traversée : <p>3<code><br>3<br>6<br>8<br>9<br>12<br>15<br>6

8

9<br>9<br>6<br>3<br>8<br>12<br>15<br>12

15

<br>3<br>8<br>6<br>15<br>12<br>9<br>Parcours de précommande : <p>9 </p>6<h2 id="">3</h2>8<p>12</p>15<p></p>Parcours post-commande : 3 8615129Évidemment, le résultat est comme prévu, nous utilisons donc le code JavaScript ci-dessus pour réaliser l'insertion de nœud dans l'arborescence , et trois méthodes de parcours, en même temps, il est évident que dans l'arbre de recherche binaire, la valeur du nœud le plus à gauche est la plus petite et la valeur du nœud le plus à droite est la plus grande, donc l'arbre de recherche binaire peut facilement obtenir les valeurs maximales et minimales Comment trouver les valeurs minimales et maximales ? En fait, il vous suffit de passer le nœud racine dans la méthode minNode/ou maxNode, puis de juger par une boucle que le nœud de gauche (minNode)/droite (maxNode) est nul Code d'implémentation :

    // 查找最小值
    this.findMin = function() {
        return minNode(root)
    }
    var minNode = function(node) {
        if (node) {
            while (node && node.left !== null) {
                node = node.left
            }
            return node.key
        }
        return null
    }
    
    // 查找最大值
    this.findMax = function() {
        return maxNode(root)
    }
    var maxNode = function (node) {
        if(node) {
            while (node && node.right !== null) {
                node =node.right
            }
            return node.key
        }
        return null
    }

所搜特定值

this.search = function(key) {
    return searchNode(root, key)
}

同样，实现它需要定义一个辅助方法,这个方法首先会检验node的合法性，如果为null，直接退出，并返回fasle。如果传入的key比当前传入node的key值小，它会继续递归查找node的左侧节点，反之，查找右侧节点。如果找到相等节点，直接退出，并返回true

    var searchNode = function(node, key) {
        if (node === null) {
            return false
        }
        if (key < node.key) {
            return searchNode(node.left, key)
        }else if (key > node.key) {
            return searchNode(node.right, key)
        }else {
            return true
        }
    }

移除节点

移除节点的实现情况比较复杂，它会有三种不同的情况：

• 
  

• 需要移除的节点是一个叶子节点

• 需要移除的节点包含一个子节点

• 需要移除的节点包含两个子节点

和实现搜索指定节点一元，要移除某个节点，必须先找到它所在的位置，因此移除方法的实现中部分代码和上面相同：

    // 移除节点
    this.remove = function(key) {
        removeNode(root,key)
    }
    var removeNode = function(node, key) {
        if (node === null) {
            return null
        }
        if (key < node.key) {
            node.left = removeNode(node.left, key)
            return node
        }else if(key > node.key) {
            node.right = removeNode(node.right,key)
            return node
        }else{
            //需要移除的节点是一个叶子节点
            if (node.left === null && node.right === null) {
                node = null
                return node
            }
            //需要移除的节点包含一个子节点
            if (node.letf === null) {
                node = node.right
                return node
            }else if (node.right === null) {
                node = node.left
                return node
            }
            //需要移除的节点包含两个子节点
            var aux = findMinNode(node.right)
            node.key = aux.key
            node.right = removeNode(node.right, axu.key)
            return node
        }
    }
    var findMinNode = function(node) {
        if (node) {
            while (node && node.left !== null) {
                node = node.left
            }
            return node
        }
        return null
    }

其中，移除包含两个子节点的节点是最复杂的情况，它包含左侧节点和右侧节点，对它进行移除主要需要三个步骤：

1. 需要找到它右侧子树中的最小节点来代替它的位置

2. 将它右侧子树中的最小节点移除

3. 将更新后的节点的引用指向原节点的父节点

有点绕儿，但必须这样，因为删除元素后的二叉搜索树必须保持它的排序性质

测试删除节点

tree.remove(8)
tree.inOrderTraverse()

打印结果：

3<br>6<br>9<br>12<br>15<br>

8 这个节点被成功删除了，但是对二叉查找树进行中序遍历依然是保持排序性质的

到这里，一个简单的二叉查找树就基本上完成了，我们为它实现了，添加、查找、删除以及先中后三种遍历方法

存在的问题

但是实际上这样的二叉查找树是存在一些问题的，当我们不断的添加更大/更小的元素的时候，会出现如下情况：

tree.insert(16)
tree.insert(17)
tree.insert(18)

来看看现在整颗树的情况：

看图片容易得出它是不平衡的，这又会引出平衡树的概念，要解决这个问题，还需要更复杂的实现，例如：AVL树，红黑树 哎，之后再慢慢去学习吧

相关文章：

二叉树遍历算法-php的示例

二叉树的中序遍历,该怎么解决

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!