Explication détaillée de l'insertion d'arbre rouge-noir et exemples de méthodes d'implémentation Javascript

Cet article vous présente principalement les informations pertinentes sur l'insertion d'arbres rouge-noir, ainsi que la méthode d'implémentation Javascript. L'article le présente en détail à travers un exemple de code. Il a une certaine valeur d'apprentissage de référence pour l'étude de chacun ou. travail. Il en a besoin. Examinons-le ensemble.

Propriétés des arbres rouge-noir

Un arbre de recherche binaire qui satisfait aux propriétés suivantes est un arbre rouge-noir

1. Chaque nœud est noir ou rouge.

2. Le nœud racine est noir.

3. Chaque nœud feuille (NIL) est noir.

4. Si un nœud est rouge, alors ses deux nœuds enfants sont noirs.

5. Pour chaque nœud, le chemin simple du nœud à tous ses nœuds feuilles descendants contient le même nombre de nœuds noirs.

Les propriétés 1 et 2 n'ont pas besoin d'être trop expliquées.

Propriété 3, chaque nœud feuille (NIL) est noir. Les nœuds feuilles ici ne font pas référence aux nœuds 1, 5, 8 et 15 dans la figure ci-dessus, mais aux nœuds avec des valeurs nulles dans la figure ci-dessous. Leur couleur est noire et ce sont les nœuds enfants de leurs nœuds parents. .

Propriété 4, si un nœud est rouge (le blanc est utilisé à la place du rouge dans l'image), alors ses deux nœuds enfants sont noirs, comme le nœud 2,5, 8,15. Cependant, si les deux nœuds enfants d'un nœud sont noirs, le nœud peut ne pas être rouge, comme le nœud 1.

Propriété 5, pour chaque nœud, le chemin simple du nœud à tous ses nœuds feuilles descendants contient le même nombre de nœuds noirs. Par exemple, sur le chemin simple du nœud 2 à tous ses nœuds feuilles descendants, le nombre de nœuds noirs est de 2 ; sur le chemin simple du nœud racine 11 à tous ses nœuds feuilles descendants, le nombre de nœuds noirs est de 2 ; .

Quelles sont les caractéristiques d’un tel arbre ?

En limitant la couleur de chaque nœud sur n'importe quel chemin simple de la racine au nœud feuille, l'arbre rouge-noir garantit qu'aucun chemin n'est deux fois plus long qu'un autre chemin. il est à peu près équilibré. ——"Introduction aux algorithmes"

En raison de la propriété 4, deux nœuds rouges ne seront pas adjacents dans un arbre rouge-noir. Le chemin le plus court possible dans l’arborescence est le chemin avec tous les nœuds noirs, et le chemin le plus long possible dans l’arborescence est le chemin avec une alternance de nœuds rouges et de nœuds noirs. Combiné avec la propriété 5, chaque chemin contient le même nombre de nœuds noirs, donc l'arbre rouge-noir garantit qu'aucun chemin ne sera deux fois plus long que les autres chemins.

Insertion de l'arbre rouge-noir

Insérez d'abord le nœud dans l'arbre de recherche binaire et coloriez-le en rouge. S'il est noir, il violera la propriété 5 et n'est pas pratique à ajuster ; s'il est rouge, il peut violer la propriété 2 ou la propriété 4. Il peut être restauré aux propriétés d'un arbre rouge-noir par des opérations relativement simples.

Après l'insertion d'un nœud dans un arbre de recherche binaire, les situations suivantes peuvent se produire :

Cas 1

Après l'insertion du nœud , il n'y a pas de nœud parent et le nœud est inséré pour devenir le nœud racine, ce qui viole la propriété 2. Le nœud est ajusté en noir pour terminer l'insertion.

Cas 2

Après l'insertion d'un nœud, son nœud parent est noir et ne viole aucune propriété. Aucun ajustement n'est requis et l'insertion est terminée. Par exemple, insérez le nœud 13 dans la figure ci-dessous.

Cas 3

Après l'insertion d'un nœud, son nœud parent est rouge, ce qui viole la propriété 4 et nécessite une série d'ajustements. Par exemple, insérez le nœud 4 dans la figure ci-dessous.

Alors, quelles sont les séries d'ajustements ?

Si le nœud parent père du nœud inséré est rouge, alors le nœud père doit avoir un grand-père de nœud parent noir, car si le nœud père n'a pas de nœud parent, c'est la racine point de nœud et le nœud racine est noir. Ensuite, l'autre nœud enfant du nœud grand-père peut être appelé le nœud oncle, qui est le nœud frère du nœud père. L'oncle du nœud peut être noir ou rouge.

Analysons d'abord la situation la plus simple, car des situations complexes peuvent être transformées en situations simples. La situation simple est la situation où l'oncle du nœud est noir.

Cas 3.1

Comme indiqué en (a) ci-dessus, la situation est la suivante, le nœud est rouge, le père est rouge, le grand-père et l'oncle sont noirs , α , β, θ, ω et η sont tous des sous-arbres correspondant aux nœuds. Supposons que dans l'ensemble de l'arbre de recherche binaire, seuls le nœud et le père ne peuvent pas devenir un arbre rouge-noir normal en raison de la violation de la propriété 4. À ce stade, l'ajustement de l'image (a) à l'image (b) peut lui redonner un arbre rouge-noir normal. arbre noir. L'ensemble du processus de réglage est en fait divisé en deux étapes : la rotation et le changement de couleur.

Qu'est-ce que la rotation ?

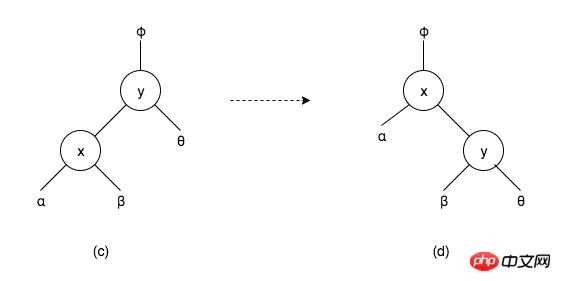
Comme le montre la figure (c) ci-dessus, il fait partie d'un arbre de recherche binaire, où x, y sont des nœuds, α, β, θ sont les sous-arbres des nœuds correspondants . On peut voir sur la figure que α < x < β < y < et la valeur du nœud y est inférieure à celle de tous les nœuds du sous-arbre θ. Dans un arbre de recherche binaire, si la valeur du nœud y est supérieure à la valeur du nœud x, alors le nœud x est dans le sous-arbre gauche du nœud y, comme le montre la figure (c) ou le nœud y est dans le sous-arbre gauche de ; nœud x Dans le sous-arbre de droite, comme le montre la figure (d). Par conséquent, α < x < β < y < Il s'agit d'une rotation qui ne détruit pas les propriétés des arbres de recherche binaires.

Le nœud est rouge, le père est rouge, le grand-père et l'oncle sont noirs. Situation spécifique 1

Dans la figure (a), le nœud est le nœud enfant gauche du père et le père est l'enfant gauche. de grand nœud, nœud < père < Dans ce cas, père < grand, cela peut être exprimé comme père est le sous-arbre gauche de grand, ou il peut être exprimé comme grand est le sous-arbre droit de père. Par conséquent, père et grand dans la figure (a) sont tournés. la rotation ne détruira pas les propriétés d'un arbre de recherche binaire, mais après la rotation, les propriétés d'un arbre rouge-noir seront détruites, la couleur des nœuds doit donc être ajustée.

Changement de couleur

Ainsi, après la rotation de l'image (a), le grand doit être changé en rouge, le père doit être changé en noir, et cela deviendra l'image (b) pour terminer l'insertion.

Le nœud est rouge, le père est rouge, le grand-père et l'oncle sont noirs. Situation spécifique 2

le nœud est le nœud enfant droit du père et le père est le nœud enfant droit de grand, comme indiqué. ci-dessous (e), se trouve le renversement de la situation spécifique 1.

C'est-à-dire, oncle

Le nœud est rouge, le père est rouge, le grand-père et l'oncle sont noirs. Situation spécifique trois

le nœud est le nœud enfant droit du père et le père est le nœud enfant gauche de grand, comme indiqué. ci-dessous ( m).

Après avoir fait pivoter le nœud et le père dans la figure (m), il devient la figure (n), et traiter le père comme un nouveau nœud devient à nouveau la situation spécifique après la rotation. et en changeant de couleur, l'insertion est terminée.

Le nœud est rouge, le père est rouge, le grand-père et l'oncle sont noirs. Situation spécifique quatre

le nœud est le nœud enfant droit du père et le père est le nœud enfant gauche de grand, comme indiqué. ci-dessous (i), se trouve le renversement de la situation spécifique trois.

Après avoir fait pivoter le nœud et le père dans la figure (i), il devient la figure (j), et traiter le père comme un nouveau nœud devient la situation spécifique 2. Encore une fois après la rotation et en changeant de couleur, l'insertion est terminée.

Cas 3.2

nœud, le père et l'oncle sont rouges, le grand-père est noir.

Comme le montre l'image ci-dessus (k), au lieu de tourner, le grand est de couleur rouge, le père et l'oncle sont noirs et le grand est utilisé comme nouveau nœud pour juger de la situation. Si grand est utilisé comme nouveau nœud, il devient le cas 2, et l'insertion est terminée ; s'il devient le cas 3.1, après ajustement, l'insertion est terminée si c'est toujours le cas 3.2, continuez à changer la couleur de grand, père ; et oncle, et nœud Le nœud monte. Si le nouveau nœud n'a pas de nœud parent, cela devient le cas 1. Le nœud racine est de couleur noire et l'insertion est terminée.

En résumé

td>

	node的情形	操作
情形1	node为红,无father	将node重新着色
情形2	node为红,father为黑
情形3.1	node,father为红,grand,uncle为黑	旋转一次或两次,并重新着色
情形3.2	node,father,uncle为红,grand为黑	将father, uncle,grand重新着色, grand作为新的node

Situation du nœud

Fonctionnement

Situation 1

Le nœud est rouge, pas de père

Recolorer le nœud

Cas 2

Le nœud est rouge et le père est noir

td>

Cas 3.1

Nœud, père est rouge, grand-père, oncle est noir

Tourner une ou deux fois et recolorer

Cas 3.2

Le nœud, le père et l'oncle sont rouges, le grand est noir

Recolorer le père, l'oncle, le grand, le grand comme un nouveau nœud

Code

// 结点
function Node(value) {
 this.value = value
 this.color = 'red' // 结点的颜色默认为红色
 this.parent = null
 this.left = null
 this.right = null
}

function RedBlackTree() {
 this.root = null
}

RedBlackTree.prototype.insert = function (node) {
 // 以二叉搜索树的方式插入结点
 // 如果根结点不存在，则结点作为根结点
 // 如果结点的值小于node，且结点的右子结点不存在，跳出循环
 // 如果结点的值大于等于node，且结点的左子结点不存在，跳出循环
 if (!this.root) {
 this.root = node
 } else {
 let current = this.root
 while (current[node.value <= current.value ? &#39;left&#39; : &#39;right&#39;]) {
  current = current[node.value <= current.value ? &#39;left&#39; : &#39;right&#39;]
 }
 current[node.value <= current.value ? &#39;left&#39; : &#39;right&#39;] = node
 node.parent = current
 }
 // 判断情形
 this._fixTree(node)
 return this
}

RedBlackTree.prototype._fixTree = function (node) {
 // 当node.parent不存在时，即为情形1，跳出循环
 // 当node.parent.color === &#39;black&#39;时，即为情形2，跳出循环
 while (node.parent && node.parent.color !== &#39;black&#39;) {
 // 情形3
 let father = node.parent
 let grand = father.parent
 let uncle = grand[grand.left === father ? &#39;right&#39; : &#39;left&#39;]
 if (!uncle || uncle.color === &#39;black&#39;) {
  // 叶结点也是黑色的
  // 情形3.1
  let directionFromFatherToNode = father.left === node ? &#39;left&#39; : &#39;right&#39;
  let directionFromGrandToFather = grand.left === father ? &#39;left&#39; : &#39;right&#39;
  if (directionFromFatherToNode === directionFromGrandToFather) {
  // 具体情形一或二
  // 旋转
  this._rotate(father)
  // 变色
  father.color = &#39;black&#39;
  grand.color = &#39;red&#39;
  } else {
  // 具体情形三或四
  // 旋转
  this._rotate(node)
  this._rotate(node)
  // 变色
  node.color = &#39;black&#39;
  grand.color = &#39;red&#39;
  }
  break // 完成插入，跳出循环
 } else {
  // 情形3.2
  // 变色
  grand.color = &#39;red&#39;
  father.color = &#39;black&#39;
  uncle.color = &#39;black&#39;
  // 将grand设为新的node
  node = grand
 }
 }

 if (!node.parent) {
 // 如果是情形1
 node.color = &#39;black&#39;
 this.root = node
 }
}

RedBlackTree.prototype._rotate = function (node) {
 // 旋转 node 和 node.parent
 let y = node.parent
 if (y.right === node) {
 if (y.parent) {
  y.parent[y.parent.left === y ? &#39;left&#39; : &#39;right&#39;] = node
 }
 node.parent = y.parent
 if (node.left) {
  node.left.parent = y
 }
 y.right = node.left
 node.left = y
 y.parent = node
 } else {
 if (y.parent) {
  y.parent[y.parent.left === y ? &#39;left&#39; : &#39;right&#39;] = node
 }
 node.parent = y.parent
 if (node.right) {
  node.right.parent = y
 }
 y.left = node.right
 node.right = y
 y.parent = node
 }
}

let arr = [11, 2, 14, 1, 7, 15, 5, 8, 4, 16]
let tree = new RedBlackTree()
arr.forEach(i => tree.insert(new Node(i)))
debugger

J'ai compilé ce qui précède pour vous, j'espère que cela vous sera utile à l'avenir.

Articles connexes :

Code à barres de progression js ajax lors du chargement

Deux solutions aux problèmes inter-domaines Ajax Méthode

Basé sur ajax, cliquez pour charger plus sans actualiser et charger sur cette page

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!