PHP utilise un tas binaire pour implémenter l'algorithme TopK

Cet article vous présente principalement la méthode d'utilisation de PHP pour implémenter l'algorithme TopK à l'aide de tas binaires. L'introduction dans l'article est très détaillée et a une certaine valeur de référence et d'apprentissage pour tous les amis qui en ont besoin peuvent suivre l'éditeur. pour apprendre ensemble.

Avant-propos

Dans le passé, j'ai souvent rencontré un problème en travaillant ou en interviewant comment obtenir un TopN massif, c'est-à-dire dans un. résultat très volumineux Pour trouver rapidement les 10 ou 100 premiers nombres les plus grands d'un ensemble, tout en garantissant l'efficacité de la mémoire et de la vitesse, notre première idée peut être d'utiliser le tri, puis d'intercepter le top 10 ou le top 100, et le tri n'est pas adapté lorsque le montant n'est pas particulièrement important. Il n'y a pas de problème, mais tant que le montant est extrêmement important, il est impossible de terminer cette tâche. Par exemple, s'il y a des centaines de millions de nombres dans un tableau ou un fichier texte, c'est le cas. impossible de tous les lire dans la mémoire, donc utiliser le tri pour résoudre ce problème n'est pas la meilleure, donc ici nous utilisons php pour implémenter un petit tas supérieur pour résoudre ce problème

Binaire. tas

Tas binaire Un tas est un type spécial de tas. Un tas binaire est un arbre binaire complet ou un arbre binaire approximativement complet. Il existe deux types de tas binaires, le tas maximum. et le tas minimum. Le tas maximum : la valeur clé du nœud parent est toujours supérieure ou égale à n'importe quel enfant. La valeur clé du nœud : la valeur clé du nœud parent est toujours inférieure ou égale à. la valeur clé de tout nœud enfant

Tas minimum-(image d'Internet)

Les tas binaires sont généralement représentés par des tableaux (voir l'image ci-dessus) Par exemple, la position du nœud racine dans le tableau est 0, et les nœuds enfants à la nième position sont respectivement à 2n+1 et 2n+2, donc les nœuds enfants à la position 0 sont à 1 et 2, le les nœuds enfants en position 1 sont en 3 et 4, et ainsi de suite. Cette méthode de stockage facilite la recherche des nœuds parents et des nœuds enfants.

Je n'entrerai pas ici dans les détails des problèmes conceptuels spécifiques. Si vous avez des questions sur les tas binaires, vous pouvez avoir une bonne compréhension de cette structure de données. Ensuite, nous utiliserons le code PHP pour l'implémenter et le résoudre. Les principaux problèmes ci-dessus. Afin de voir la différence, utilisons d'abord la méthode de tri pour l'implémenter et voyons comment elle fonctionne.

Utilisez l'algorithme de tri rapide pour implémenter TopN

//为了测试运行内存调大一点
ini_set('memory_limit', '2024M');

//实现一个快速排序函数
function quick_sort(array $array){
 $length = count($array);
 $left_array = array();
 $right_array = array();
 if($length <= 1){
  return $array;
 }
 $key = $array[0];
 for($i=1;$i<$length;$i++){
  if($array[$i] > $key){
   $right_array[] = $array[$i];
  }else{
   $left_array[] = $array[$i];
  }
 }
 $left_array = quick_sort($left_array);
 $right_array = quick_sort($right_array);
 return array_merge($right_array,array($key),$left_array); 
}

//构造500w不重复数
for($i=0;$i<5000000;$i++){
 $numArr[] = $i; 
}
//打乱它们
shuffle($numArr);

//现在我们从里面找到top10最大的数
var_dump(time());
print_r(array_slice(quick_sort($all),0,10));
var_dump(time());

Résultat après l'exécution

Vous pouvez voir que les 10 meilleurs résultats sont imprimés ci-dessus et que le temps d'exécution est affiché, qui est d'environ 99 s, mais c'est seulement 5 millions Si tous les nombres peuvent être chargés dans la mémoire, si nous avons un fichier avec 5 kW ou 500 millions de nombres, il y aura certainement des problèmes.

Utilisez l'algorithme du tas binaire pour implémenter TopN

Le processus de mise en œuvre est le suivant :

1. Lisez d'abord 10 ou 100 nombres dans le tableau, Il s'agit de notre numéro topN.

2. Appelez la fonction générer un petit tas supérieur pour générer une petite structure de tas supérieur à partir de ce tableau. À ce stade, le haut du tas doit être le plus petit.

3. Parcourez tous les nombres restants du fichier ou du tableau dans l'ordre

4. Comparez la taille de chaque élément parcouru avec l'élément en haut du tas. . S'il est plus petit que l'élément en haut du tas, jetez-le. S'il est plus grand que l'élément supérieur du tas, remplacez-le

5. Après avoir remplacé l'élément supérieur. du tas, appelez la fonction générer un petit tas supérieur pour continuer à générer le petit tas supérieur, car vous devez trouver le plus petit.

6. Répétez les étapes 4 à 5 ci-dessus, de sorte qu'après toutes les traversées sont terminées, le plus grand topN sera dans notre petit tas supérieur, car notre petit tas supérieur exclura toujours le plus petit et le plus grand, et la vitesse d'ajustement du petit tas supérieur est également très rapide. ajustement, tant que le nœud racine est plus petit que les nœuds gauche et droit

7. En termes de complexité de l'algorithme, c'est le pire des cas dans le top 10. Ensuite, chaque fois qu'un nombre est. parcouru, s'il est remplacé par le haut du tas, il doit être ajusté 10 fois, ce qui est plus rapide que le tri, et tout le contenu n'est pas lu dans la mémoire. On peut comprendre que la réalisation est un parcours linéaire.

//生成小顶堆函数
function Heap(&$arr,$idx){
 $left = ($idx << 1) + 1;
 $right = ($idx << 1) + 2;

 if (!$arr[$left]){
  return;
 }

 if($arr[$right] && $arr[$right] < $arr[$left]){
  $l = $right;
 }else{
  $l = $left;
 }

 if ($arr[$idx] > $arr[$l]){
   $tmp = $arr[$idx]; 
   $arr[$idx] = $arr[$l];
   $arr[$l] = $tmp;
   Heap($arr,$l);
 }
}

//这里为了保证跟上面一致，也构造500w不重复数
/*
 当然这个数据集并不一定全放在内存，也可以在
 文件里面，因为我们并不是全部加载到内存去进
 行排序
*/
for($i=0;$i<5000000;$i++){
 $numArr[] = $i; 
}
//打乱它们
shuffle($numArr);

//先取出10个到数组
$topArr = array_slice($numArr,0,10);

//获取最后一个有子节点的索引位置
//因为在构造小顶堆的时候是从最后一个有左或右节点的位置
//开始从下往上不断的进行移动构造（具体可看上面的图去理解）
$idx = floor(count($topArr) / 2) - 1;

//生成小顶堆
for($i=$idx;$i>=0;$i--){
 Heap($topArr,$i);
}

var_dump(time());
//这里可以看到，就是开始遍历剩下的所有元素
for($i = count($topArr); $i < count($numArr); $i++){
 //每遍历一个则跟堆顶元素进行比较大小
 if ($numArr[$i] > $topArr[0]){
  //如果大于堆顶元素则替换
  $topArr[0] = $numArr[$i];
  /*
   重新调用生成小顶堆函数进行维护，只不过这次是从堆顶
   的索引位置开始自上往下进行维护，因为我们只是把堆顶
   的元素给替换掉了而其余的还是按照根节点小于左右节点
   的顺序摆放这也就是我们上面说的，只是相对调整下，并
   不是全部调整一遍
  */
  Heap($topArr,0);
 }
}
var_dump(time());

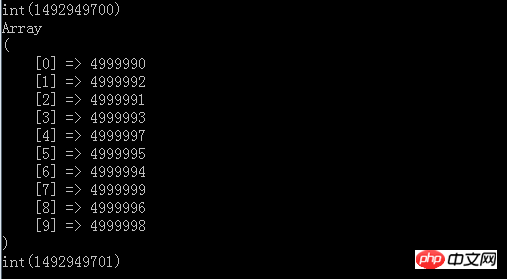
Après avoir exécuté le résultat

vous pouvez voir le résultat final Il fait également partie du top 10, mais cela ne prend qu'environ 1 seconde, et l'efficacité de la mémoire et du temps répond à nos exigences. Et la meilleure chose à propos du tri est que nous n'avons pas besoin de lire tous les ensembles de données dans la mémoire. , parce que nous n'avons pas besoin de trier, et ce qui précède est à titre de démonstration, donc 5 millions d'éléments sont construits directement dans la mémoire. Cependant, nous pouvons transférer tout cela dans le fichier, puis lire et comparer ligne par ligne, car. le point central de notre structure de données est le parcours linéaire. Comparez-le avec la petite structure de tas supérieur dans la mémoire et obtenez enfin TopN.

Ce qui précède représente l’intégralité du contenu de cet article, j’espère qu’il sera utile à l’étude de chacun.

Recommandations associées :

php pour acquérir des compétences de conversion_php hexadécimales

Comment compiler Redis et PHPredis sous Linux_php conseils

PHPComment utiliser la bibliothèque de classes Mysqli pour obtenir un effet de pagination parfait_php conseils

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!