Explication détaillée des étapes pour implémenter l'algorithme de tri par fusion en PHP

Cette fois, je vais vous apporter une explication détaillée des étapes pour implémenter l'algorithme de tri par fusion en PHP. Quelles sont les précautions pour que PHP implémente l'algorithme de tri par fusion. Voici des cas pratiques, prenons. un regard.

Idée de base :

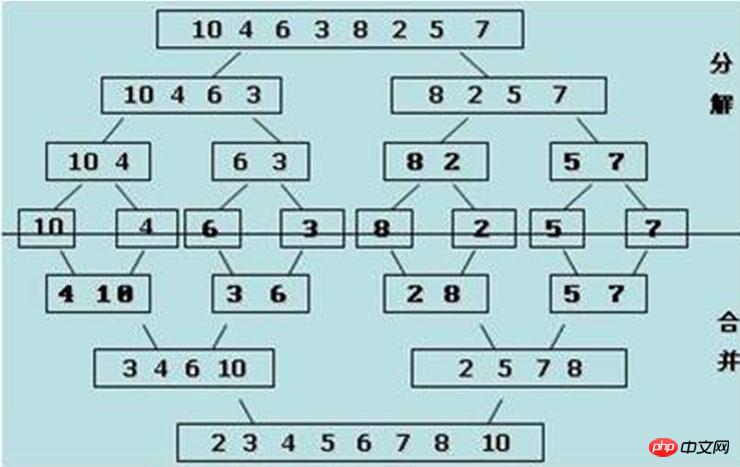
Tri par fusion : C'est une méthode de tri mise en œuvre en utilisant l'idée de fusion (fusion). Son principe est qu'en supposant que la séquence initiale contient n éléments, elle peut être considérée comme n sous-séquences ordonnées, chaque sous-séquence a une longueur de 1, puis fusionnée par paires pour obtenir ⌈ n / 2⌉ (⌈ x ⌉ signifie non Le plus petit entier inférieur au tri par fusion bidirectionnel.

1. Le processus de fusion :

a[i] prend la partie avant du tableau a (déjà trié), a[j] prend la dernière partie de la partie du tableau a (déjà triée)

le tableau r stocke le tableau a trié

compare les tailles de a[i] et a[j], si a[i] ≤ a[ j ], puis copiez l'élément a[i] dans la première liste ordonnée dans r[k], et ajoutez 1 à i et k respectivement ; sinon, copiez l'élément a[j] dans la deuxième liste ordonnée. Copiez-le dans r[ ; k], et ajoutez 1 à j et k respectivement. Ce cycle continue jusqu'à ce que l'une des listes ordonnées soit récupérée, puis copie les éléments restants de l'autre liste ordonnée vers r de l'indice k vers l'élément de l'indice t. Nous utilisons généralement la récursion pour implémenter l'algorithme de tri par fusion. Tout d'abord, divisez l'intervalle à trier [s, t] en deux au milieu, puis triez la sous-plage de gauche, puis triez la sous-plage de droite et enfin effectuez une sous-plage de gauche. opération de fusion sur les intervalles gauche et droit Fusionner en intervalles ordonnés [s,t].

2. Opération de fusion :

L'opération de fusion (fusion), également appelée algorithme de fusion, fait référence à la méthode de fusion de deux séquences séquentielles en une seule séquence séquentielle.

S'il existe une séquence {6, 202, 100, 301, 38, 8, 1>

État initial : 6, 202, 100, 301, 38, 8, 1

Après la première fusion : {6,202}, {100,301}, {8,38}, {1}, nombre de comparaisons : 3

Après la deuxième fusion : {6,100,202,301}, {1 ; ,8,38}, nombre de comparaisons : 4 ;

Après la troisième fusion : {1,6,8,38,100,202,301}, nombre de comparaisons :

Le nombre total de comparaisons est : 3+4+4=11,;

Le nombre inverse est 14 ;

Description de l'algorithme :

Le principe de fonctionnement de. l'opération de fusion est la suivante :

Étape 1 : Demander de l'espace pour que sa taille soit la somme des deux séquences triées. Cet espace est utilisé pour stocker la séquence fusionnée

Étape 2 : Définissez deux pointeurs. Les positions initiales sont les positions de départ des deux séquences triées

Étape 3 : Comparez les éléments pointés par les deux pointeurs, sélectionnez l'élément relativement petit et placez-le dans l'espace de fusion, puis déplacez-le. le pointeur vers la position suivante

Répétez l'étape 3 jusqu'à ce qu'un pointeur dépasse la fin de la séquence

Copiez tous les éléments restants de l'autre séquence directement à la fin de la séquence fusionnée

Implémentation de l'algorithme :

Jetons d'abord un coup d'œil à la partie fonction principale :

//交换函数
function swap(array &$arr,$a,$b){
  $temp = $arr[$a];
  $arr[$a] = $arr[$b];
  $arr[$b] = $temp;
}
//归并算法总函数
function MergeSort(array &$arr){
  $start = 0;
  $end = count($arr) - 1;
  MSort($arr,$start,$end);
}

Dans la fonction totale, nous appelons uniquement une fonction MSort(), car nous voulons utiliser des appels récursifs, MSort() est encapsulé.

Jetons un coup d'œil à la fonction MSort() :

function MSort(array &$arr,$start,$end){
  //当子序列长度为1时，$start == $end，不用再分组
  if($start < $end){
    $mid = floor(($start + $end) / 2); //将 $arr 平分为 $arr[$start - $mid] 和 $arr[$mid+1 - $end]
    MSort($arr,$start,$mid);  //将 $arr[$start - $mid] 归并为有序的$arr[$start - $mid]
    MSort($arr,$mid + 1,$end);  //将 $arr[$mid+1 - $end] 归并为有序的 $arr[$mid+1 - $end]
    Merge($arr,$start,$mid,$end);    //将$arr[$start - $mid]部分和$arr[$mid+1 - $end]部分合并起来成为有序的$arr[$start - $end]
  }
}

La fonction MSort() ci-dessus implémente la division du tableau en deux, puis à nouveau en deux (jusqu'à ce que la longueur de la sous-séquence soit de 1 ), puis les sous-séquences sont combinées.

C'est maintenant notre fonction d'opération de fusion Merge() :

//归并操作
function Merge(array &$arr,$start,$mid,$end){
  $i = $start;
  $j=$mid + 1;
  $k = $start;
  $temparr = array();
  while($i!=$mid+1 && $j!=$end+1)
  {
    if($arr[$i] >= $arr[$j]){
      $temparr[$k++] = $arr[$j++];
    }
    else{
      $temparr[$k++] = $arr[$i++];
    }
  }
  //将第一个子序列的剩余部分添加到已经排好序的 $temparr 数组中
  while($i != $mid+1){
    $temparr[$k++] = $arr[$i++];
  }
  //将第二个子序列的剩余部分添加到已经排好序的 $temparr 数组中
  while($j != $end+1){
    $temparr[$k++] = $arr[$j++];
  }
  for($i=$start; $i<=$end; $i++){
    $arr[$i] = $temparr[$i];
  }
}

À ce stade, notre algorithme de fusion est terminé. Essayons d'appeler :

$arr = array(9,1,5,8,3,7,4,6,2);
MergeSort($arr);
var_dump($arr);

Résultats en cours d'exécution :

array(9) {
 [0]=>
 int(1)
 [1]=>
 int(2)
 [2]=>
 int(3)
 [3]=>
 int(4)
 [4]=>
 int(5)
 [5]=>
 int(6)
 [6]=>
 int(7)
 [7]=>
 int(8)
 [8]=>
 int(9)
}

Analyse de complexité :

En raison de la fusion de The L'algorithme regroupera et comparera, que la séquence d'origine soit ordonnée ou non, de sorte que sa meilleure, sa pire complexité temporelle et sa complexité temporelle moyenne sont O(nlogn).

L'algorithme de fusion est un algorithme de tri stable.

Je pense que vous maîtrisez la méthode après avoir lu le cas dans cet article. Pour des informations plus intéressantes, veuillez prêter attention aux autres articles connexes sur le site Web chinois de php !

Lecture recommandée :

Explication détaillée des cas d'utilisation du mode PHP singleton

php+receivemail permet d'envoyer et de recevoir des emails

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!