Python dessine des graphiques 3D

Cet article présente principalement Python pour dessiner des graphiques 3D, qui a une certaine valeur de référence. Maintenant, je le partage avec tout le monde. Les amis dans le besoin peuvent s'y référer

Les graphiques 3D sont utilisés dans l'analyse des données, la modélisation des données, et les graphiques. Il est largement utilisé dans des domaines tels que le traitement d'images et le traitement d'images. Ci-dessous, je vais vous présenter comment utiliser Python pour dessiner des graphiques 3D, y compris le dessin de points de dispersion 3D, de surfaces 3D, de contours 3D, de lignes droites 3D ( courbes) et texte 3D.

Travail de préparation :

Pour dessiner des graphiques 3D en python, vous utilisez toujours le module de dessin couramment utilisé matplotlib, mais vous devez installer la boîte à outils mpl_toolkits. La méthode d'installation est la suivante : entrez le. répertoire d'installation de python depuis la ligne de commande Windows Dans le dossier Scripts, exécutez : pip install --upgrade matplotlib; exécutez cette commande directement dans l'environnement Linux.

Après avoir installé ce module, vous pouvez appeler la classe mplot3d sous mpl_tookits pour dessiner des graphiques 3D.

Ce qui suit est un exemple.

1. Dessin de la forme de la surface 3D

from mpl_toolkits.mplot3d import Axes3D 
import matplotlib.pyplot as plt 
import numpy as np 
 
fig = plt.figure() 
ax = fig.add_subplot(111, projection='3d') 
 
# Make data 
u = np.linspace(0, 2 * np.pi, 100) 
v = np.linspace(0, np.pi, 100) 
x = 10 * np.outer(np.cos(u), np.sin(v)) 
y = 10 * np.outer(np.sin(u), np.sin(v)) 
z = 10 * np.outer(np.ones(np.size(u)), np.cos(v)) 
 
# Plot the surface 
ax.plot_surface(x, y, z, color='b') 
 
plt.show()

Surface de la sphère, les résultats sont les suivants :

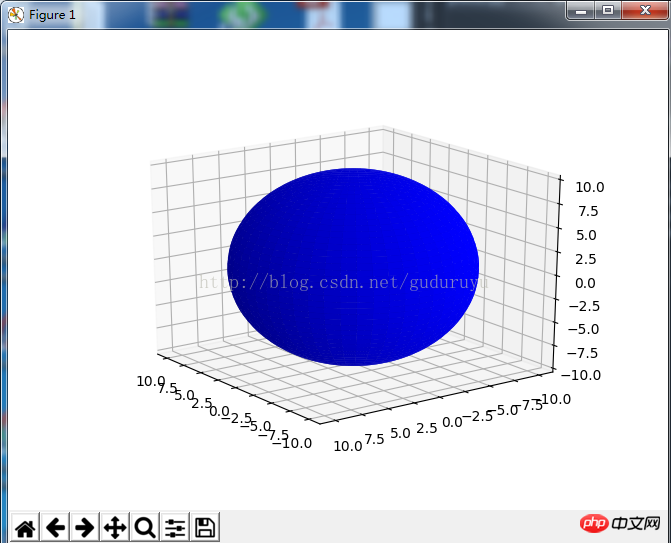
2. Dessin de lignes droites (courbes) 3D

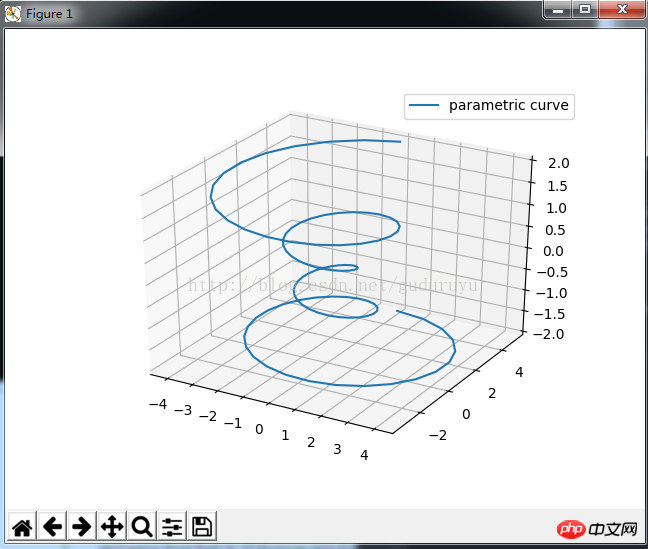
import matplotlib as mpl 
from mpl_toolkits.mplot3d import Axes3D 
import numpy as np 
import matplotlib.pyplot as plt 
 
mpl.rcParams['legend.fontsize'] = 10 
 
fig = plt.figure() 
ax = fig.gca(projection='3d') 
theta = np.linspace(-4 * np.pi, 4 * np.pi, 100) 
z = np.linspace(-2, 2, 100) 
r = z**2 + 1 
x = r * np.sin(theta) 
y = r * np.cos(theta) 
ax.plot(x, y, z, label='parametric curve') 
ax.legend() 
 
plt.show()

Ce code permet de dessiner une spirale Courbe 3D. Les résultats sont les suivants :

3. Dessinez des contours 3D

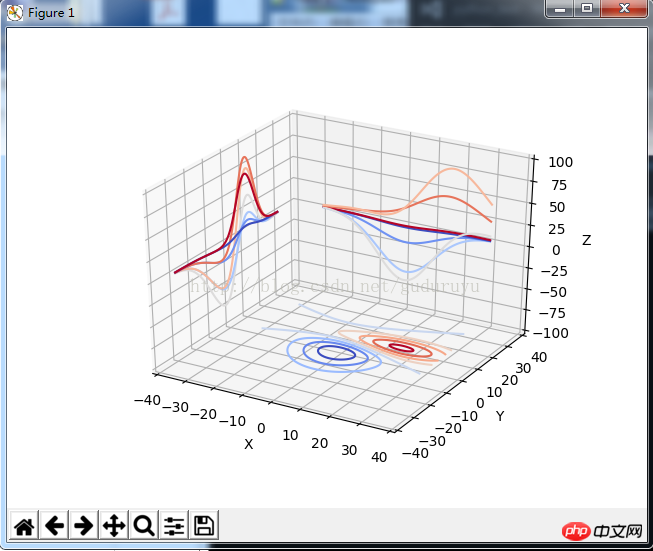
from mpl_toolkits.mplot3d import axes3d 
import matplotlib.pyplot as plt 
from matplotlib import cm 
 
fig = plt.figure() 
ax = fig.gca(projection='3d') 
X, Y, Z = axes3d.get_test_data(0.05) 
cset = ax.contour(X, Y, Z, zdir='z', offset=-100, cmap=cm.coolwarm) 
cset = ax.contour(X, Y, Z, zdir='x', offset=-40, cmap=cm.coolwarm) 
cset = ax.contour(X, Y, Z, zdir='y', offset=40, cmap=cm.coolwarm) 
 
ax.set_xlabel('X') 
ax.set_xlim(-40, 40) 
ax.set_ylabel('Y') 
ax.set_ylim(-40, 40) 
ax.set_zlabel('Z') 
ax.set_zlim(-100, 100) 
 
plt.show()

.

Les résultats du dessin sont les suivants :

4. Dessinez un histogramme 3D

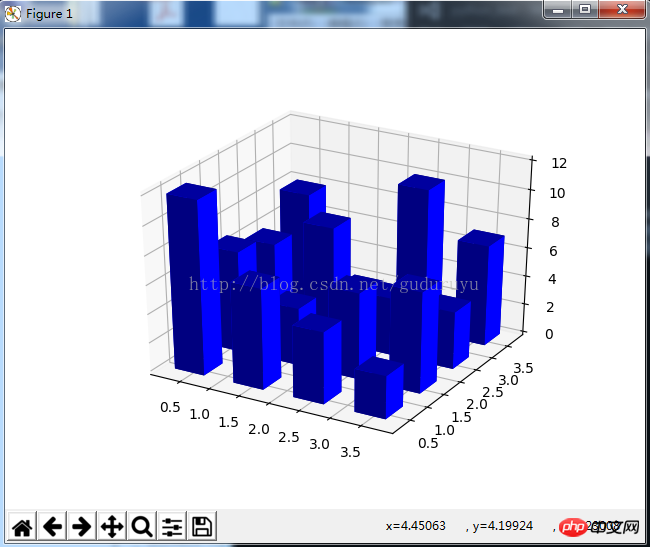
from mpl_toolkits.mplot3d import Axes3D 
import matplotlib.pyplot as plt 
import numpy as np 
 
fig = plt.figure() 
ax = fig.add_subplot(111, projection='3d') 
x, y = np.random.rand(2, 100) * 4 
hist, xedges, yedges = np.histogram2d(x, y, bins=4, range=[[0, 4], [0, 4]]) 
 
# Construct arrays for the anchor positions of the 16 bars. 
# Note: np.meshgrid gives arrays in (ny, nx) so we use 'F' to flatten xpos, 
# ypos in column-major order. For numpy >= 1.7, we could instead call meshgrid 
# with indexing='ij'. 
xpos, ypos = np.meshgrid(xedges[:-1] + 0.25, yedges[:-1] + 0.25) 
xpos = xpos.flatten('F') 
ypos = ypos.flatten('F') 
zpos = np.zeros_like(xpos) 
 
# Construct arrays with the dimensions for the 16 bars. 
dx = 0.5 * np.ones_like(zpos) 
dy = dx.copy() 
dz = hist.flatten() 
 
ax.bar3d(xpos, ypos, zpos, dx, dy, dz, color='b', zsort='average') 
 
plt.show()

Les résultats du dessin sont les suivants :

5. Dessinez des lignes de maillage 3D

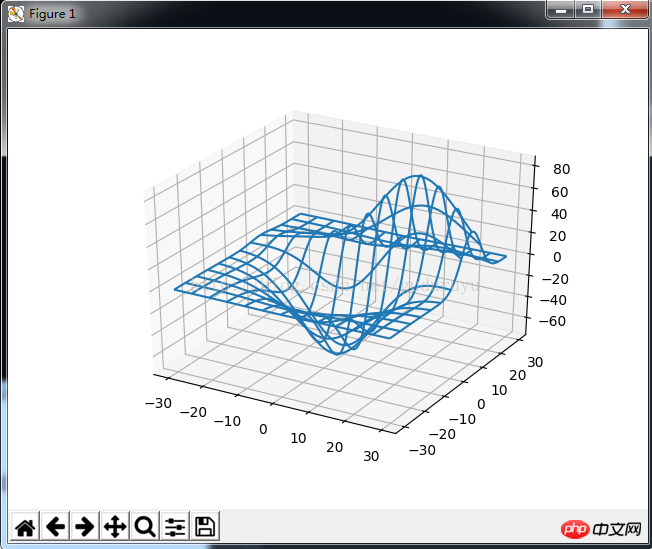
from mpl_toolkits.mplot3d import axes3d 
import matplotlib.pyplot as plt 
 
 
fig = plt.figure() 
ax = fig.add_subplot(111, projection='3d') 
 
# Grab some test data. 
X, Y, Z = axes3d.get_test_data(0.05) 
 
# Plot a basic wireframe. 
ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10) 
 
plt.show()

.

Les résultats du dessin sont les suivants :

6. Dessinez un diagramme de patch triangulaire 3D

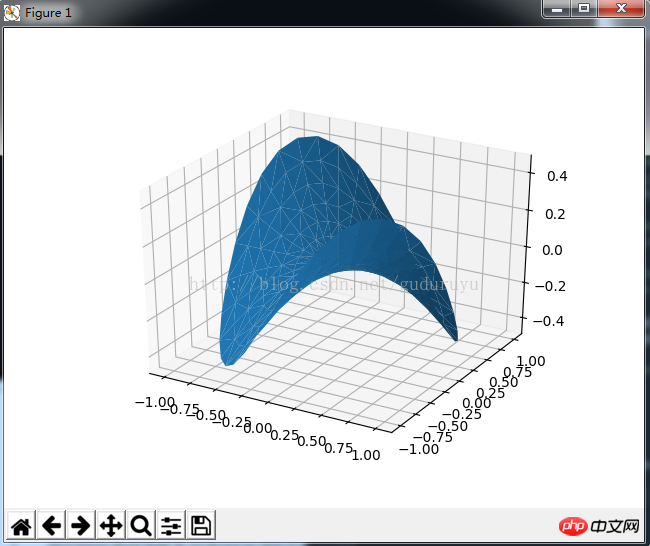
from mpl_toolkits.mplot3d import Axes3D 
import matplotlib.pyplot as plt 
import numpy as np 
 
 
n_radii = 8 
n_angles = 36 
 
# Make radii and angles spaces (radius r=0 omitted to eliminate duplication). 
radii = np.linspace(0.125, 1.0, n_radii) 
angles = np.linspace(0, 2*np.pi, n_angles, endpoint=False) 
 
# Repeat all angles for each radius. 
angles = np.repeat(angles[..., np.newaxis], n_radii, axis=1) 
 
# Convert polar (radii, angles) coords to cartesian (x, y) coords. 
# (0, 0) is manually added at this stage, so there will be no duplicate 
# points in the (x, y) plane. 
x = np.append(0, (radii*np.cos(angles)).flatten()) 
y = np.append(0, (radii*np.sin(angles)).flatten()) 
 
# Compute z to make the pringle surface. 
z = np.sin(-x*y) 
 
fig = plt.figure() 
ax = fig.gca(projection='3d') 
 
ax.plot_trisurf(x, y, z, linewidth=0.2, antialiased=True) 
 
plt.show(

Les résultats du dessin sont les suivants :

7. Dessinez un nuage de points 3D

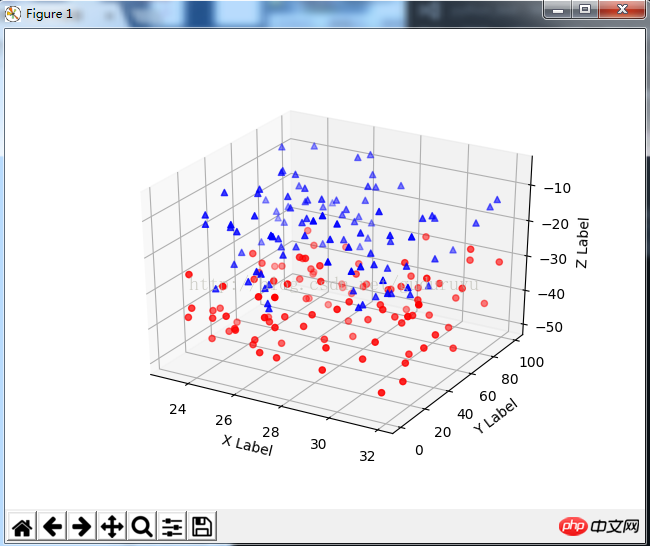
from mpl_toolkits.mplot3d import Axes3D 
import matplotlib.pyplot as plt 
import numpy as np 
 
 
def randrange(n, vmin, vmax): 
 ''''' 
 Helper function to make an array of random numbers having shape (n, ) 
 with each number distributed Uniform(vmin, vmax). 
 ''' 
 return (vmax - vmin)*np.random.rand(n) + vmin 
 
fig = plt.figure() 
ax = fig.add_subplot(111, projection='3d') 
 
n = 100 
 
# For each set of style and range settings, plot n random points in the box 
# defined by x in [23, 32], y in [0, 100], z in [zlow, zhigh]. 
for c, m, zlow, zhigh in [('r', 'o', -50, -25), ('b', '^', -30, -5)]: 
 xs = randrange(n, 23, 32) 
 ys = randrange(n, 0, 100) 
 zs = randrange(n, zlow, zhigh) 
 ax.scatter(xs, ys, zs, c=c, marker=m) 
 
ax.set_xlabel('X Label') 
ax.set_ylabel('Y Label') 
ax.set_zlabel('Z Label') 
 
plt.show()

Les résultats du dessin sont les suivants :

8. Dessinez du texte 3D

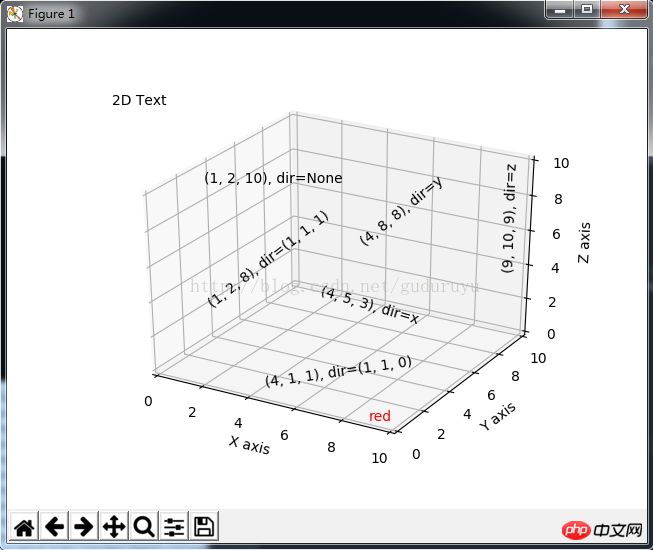
from mpl_toolkits.mplot3d import Axes3D 
import matplotlib.pyplot as plt 
 
 
fig = plt.figure() 
ax = fig.gca(projection='3d') 
 
# Demo 1: zdir 
zdirs = (None, 'x', 'y', 'z', (1, 1, 0), (1, 1, 1)) 
xs = (1, 4, 4, 9, 4, 1) 
ys = (2, 5, 8, 10, 1, 2) 
zs = (10, 3, 8, 9, 1, 8) 
 
for zdir, x, y, z in zip(zdirs, xs, ys, zs): 
 label = '(%d, %d, %d), dir=%s' % (x, y, z, zdir) 
 ax.text(x, y, z, label, zdir) 
 
# Demo 2: color 
ax.text(9, 0, 0, "red", color='red') 
 
# Demo 3: text2D 
# Placement 0, 0 would be the bottom left, 1, 1 would be the top right. 
ax.text2D(0.05, 0.95, "2D Text", transform=ax.transAxes) 
 
# Tweaking display region and labels 
ax.set_xlim(0, 10) 
ax.set_ylim(0, 10) 
ax.set_zlim(0, 10) 
ax.set_xlabel('X axis') 
ax.set_ylabel('Y axis') 
ax.set_zlabel('Z axis') 
 
plt.show(

Résultat du dessin Comme suit :

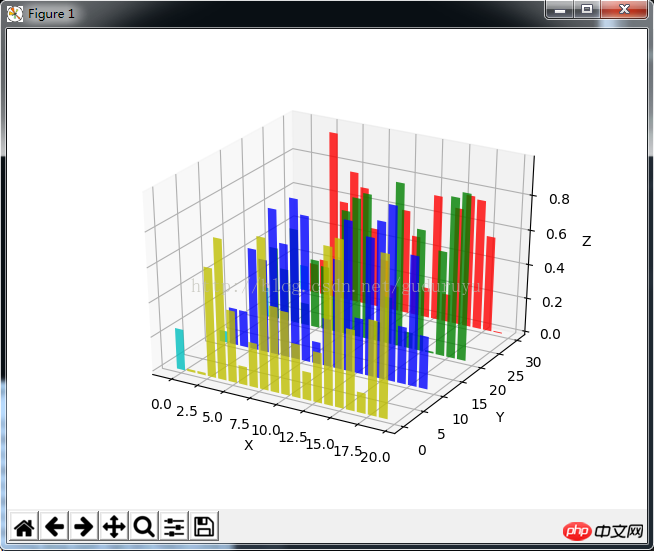
9. Graphique à barres 3D

from mpl_toolkits.mplot3d import Axes3D 
import matplotlib.pyplot as plt 
import numpy as np 
 
fig = plt.figure() 
ax = fig.add_subplot(111, projection='3d') 
for c, z in zip(['r', 'g', 'b', 'y'], [30, 20, 10, 0]): 
 xs = np.arange(20) 
 ys = np.random.rand(20) 
 
 # You can provide either a single color or an array. To demonstrate this, 
 # the first bar of each set will be colored cyan. 
 cs = [c] * len(xs) 
 cs[0] = 'c' 
 ax.bar(xs, ys, zs=z, zdir='y', color=cs, alpha=0.8) 
 
ax.set_xlabel('X') 
ax.set_ylabel('Y') 
ax.set_zlabel('Z') 
 
plt.show()

Les résultats du tirage sont les suivants :

Recommandations associées :

Utilisez Python pour dessiner des graphiques couramment utilisés

Utilisez une explication détaillée d'exemples de dessin de graphiques en python

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!