Maison >développement back-end >Tutoriel Python >Comment TensorFlow met en œuvre l'entraînement aléatoire et l'entraînement par lots
Comment TensorFlow met en œuvre l'entraînement aléatoire et l'entraînement par lots
- 不言original
- 2018-04-28 10:00:452728parcourir
Cet article présente principalement la méthode de TensorFlow pour implémenter l'entraînement aléatoire et l'entraînement par lots. Maintenant, je le partage avec vous et le donne comme référence. Venez jeter un œil ensemble
TensorFlow met à jour les variables du modèle. Il peut fonctionner sur un point de données à la fois ou sur de grandes quantités de données à la fois. Opérer sur un seul exemple de formation peut conduire à un processus d'apprentissage « original », mais la formation avec de gros lots peut être coûteuse en termes de calcul. Le type de formation choisi est très critique pour la convergence de l’algorithme d’apprentissage automatique.
Pour que TensorFlow puisse calculer des gradients variables pour que la rétropropagation fonctionne, nous devons mesurer la perte sur un ou plusieurs échantillons.
L'entraînement aléatoire échantillonnera de manière aléatoire les données d'entraînement et ciblera les paires de données à la fois pour terminer l'entraînement. Une autre option consiste à faire la moyenne de la perte pour le calcul du gradient dans une formation par lots importants, et la taille de la formation par lots peut être étendue à l'ensemble des données en même temps. Nous montrons ici comment étendre l'exemple précédent d'un algorithme de régression - en utilisant un entraînement aléatoire et un entraînement par lots.
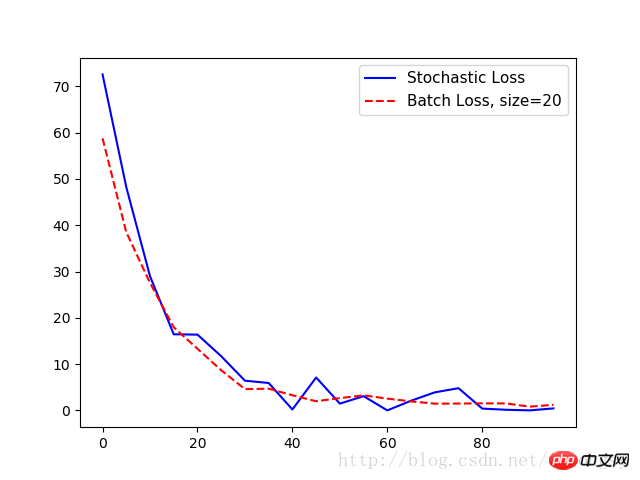
La formation par lots et la formation aléatoire diffèrent par leurs méthodes d'optimisation et leur convergence.
# 随机训练和批量训练
#----------------------------------
#
# This python function illustrates two different training methods:
# batch and stochastic training. For each model, we will use
# a regression model that predicts one model variable.
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from tensorflow.python.framework import ops
ops.reset_default_graph()
# 随机训练:
# Create graph
sess = tf.Session()
# 声明数据
x_vals = np.random.normal(1, 0.1, 100)
y_vals = np.repeat(10., 100)
x_data = tf.placeholder(shape=[1], dtype=tf.float32)
y_target = tf.placeholder(shape=[1], dtype=tf.float32)
# 声明变量 (one model parameter = A)
A = tf.Variable(tf.random_normal(shape=[1]))
# 增加操作到图
my_output = tf.multiply(x_data, A)
# 增加L2损失函数
loss = tf.square(my_output - y_target)
# 初始化变量
init = tf.global_variables_initializer()
sess.run(init)
# 声明优化器
my_opt = tf.train.GradientDescentOptimizer(0.02)
train_step = my_opt.minimize(loss)
loss_stochastic = []
# 运行迭代
for i in range(100):
rand_index = np.random.choice(100)
rand_x = [x_vals[rand_index]]
rand_y = [y_vals[rand_index]]
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
if (i+1)%5==0:
print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)))
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})
print('Loss = ' + str(temp_loss))
loss_stochastic.append(temp_loss)
# 批量训练:
# 重置计算图
ops.reset_default_graph()
sess = tf.Session()
# 声明批量大小
# 批量大小是指通过计算图一次传入多少训练数据
batch_size = 20
# 声明模型的数据、占位符
x_vals = np.random.normal(1, 0.1, 100)
y_vals = np.repeat(10., 100)
x_data = tf.placeholder(shape=[None, 1], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
# 声明变量 (one model parameter = A)
A = tf.Variable(tf.random_normal(shape=[1,1]))
# 增加矩阵乘法操作(矩阵乘法不满足交换律)
my_output = tf.matmul(x_data, A)
# 增加损失函数
# 批量训练时损失函数是每个数据点L2损失的平均值
loss = tf.reduce_mean(tf.square(my_output - y_target))
# 初始化变量
init = tf.global_variables_initializer()
sess.run(init)
# 声明优化器
my_opt = tf.train.GradientDescentOptimizer(0.02)
train_step = my_opt.minimize(loss)
loss_batch = []
# 运行迭代
for i in range(100):
rand_index = np.random.choice(100, size=batch_size)
rand_x = np.transpose([x_vals[rand_index]])
rand_y = np.transpose([y_vals[rand_index]])
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
if (i+1)%5==0:
print('Step #' + str(i+1) + ' A = ' + str(sess.run(A)))
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})
print('Loss = ' + str(temp_loss))
loss_batch.append(temp_loss)
plt.plot(range(0, 100, 5), loss_stochastic, 'b-', label='Stochastic Loss')
plt.plot(range(0, 100, 5), loss_batch, 'r--', label='Batch Loss, size=20')
plt.legend(loc='upper right', prop={'size': 11})
plt.show()
Sortie :
Étape #5 A = [ 1.47604525]
Perte = [ 72.55678558]
Étape n°10 A = [ 3.01128507]
Perte = [ 48.22986221]
Étape n°15 A = [ 4.27042341]
Perte = [ 28.97912598]
Étape n°20 A = [ 5.2984333]
Perte = [ 16.44779968]
Étape #25 A = [ 6.17473984]
Perte = [ 16.373312]
Étape #30 A = [ 6.89866304]
Perte = [ 11.71054649]
Étape #35Un = [ 7.39849901]
Perte = [ 6.42773056]
Étape #40 A = [ 7.84618378]
Perte = [ 5.92940331]
Étape #45 A = [ 8.15709782]
Perte = [ 0 . 2142024]
Étape #50 A = [ 8.54818344]
Perte = [ 7.11651039]
Étape #55 A = [ 8.82354641]
Perte = [ 1.47823763]
Étape #60 A = [ .07896614 ]
Perte = [ 3.08244276]
Étape #65 A = [ 9.24868107]
Perte = [ 0.01143846]
Étape #70 A = [ 9.36772251]
Perte = [ ]
Étape #75 A = [ 9.49171734]
Perte = [ 3.90913701]
Étape #80 A = [ 9.6622715]
Perte = [ 4.80727625]
Étape #85 A = [ 9.73786926]
Perte = [ 0,39915398]
Étape n°90 A = [ 9,81853104]
Perte = [ 0,14876099]
Étape n°95 A = [ 9,90371323]
Perte = [ 0,01657014]
Étape n°10 0A = [ 9.86669159 ]
Perte = [ 0.444787]
Étape #5 A = [[ 2.34371352]]
Perte = 58.766
Étape #10 A = [[ 3.74766445]]
Perte = 38.48 75
Étape #15 A = [[ 4.88928795]]
Perte = 27.5632
Étape #20 A = [[ 5.82038736]]
Perte = 17.9523
Étape #25 A = [[ 6.58999157]]
Perte = 13,3245
Étape n°30 A = [[ 7,20851326]]
Perte = 8,68099
Étape n°35 A = [[ 7,71694899]]
Perte = 4,60659
Étape n°40 A = [[8.1296711]]
Perte = 4.70107
Étape #45 A = [[8.47107315]
Perte = 3.28318
Étape #50 A = [[8.74283409]]
Perte = 1.99057
Étape #55 A = [[ 8.98811722]]
Perte = 2.66906
Étape #60 A = [[ 9.18062305]]
Perte = 3.26207
Étape #65 A = [[ 9.3165 5025 ]]
Perte = 2,55459
Étape #70 A = [[ 9,43130589]]
Perte = 1,95839
Étape #75 A = [[ 9,55670166]]
Perte = 1,46504
Étape #80 A = [[ 9.6354847]]
Perte = 1.49021
Étape #85 A = [[ 9.73470974]]
Perte = 1.53289
Étape #90 A = [[ 9.77956581]]
Perte = 1,52173
Étape #95 A = [[ 9,83666706]]
Perte = 0,819207
Étape #100 A = [[ 9,85569191]]
Perte = 1,2197
| 训练类型 | 优点 | 缺点 |
|---|---|---|
| 随机训练 | 脱离局部最小 | 一般需更多次迭代才收敛 |
| 批量训练 | 快速得到最小损失 | 耗费更多计算资源 |
Recommandations associées :
Une brève discussion sur la sauvegarde et la restauration du modèle Tensorflow
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

