Explication détaillée de la programmation Python pour calculer des intégrales définies via la méthode de Monte Carlo

Cet article présente principalement l'explication détaillée du calcul des intégrales définies via la méthode de Monte Carlo dans la programmation Python. Il a une certaine valeur de référence et les amis dans le besoin peuvent s'y référer.

Je pense qu'à l'époque, lorsque je passais l'examen d'entrée aux études supérieures, j'aurais aimé savoir qu'il existait une si bonne chose que le calcul d'intégrales définies. . . Je plaisante, calculer des intégrales définies n’était pas si simple à l’époque. Mais cela m’a donné l’idée d’utiliser des langages de programmation pour résoudre des problèmes mathématiques plus complexes. Venons-en au fait.

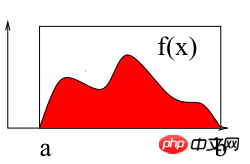
Comme le montre la figure ci-dessus, calculer l'intégrale de f(x) sur l'intervalle [a b] revient à trouver l'aire de la zone rouge délimitée par le courbe et l’axe X. Ce qui suit utilise la méthode de Monte Carlo pour calculer l'intégrale définie sur l'intervalle [2 3] : ∫(x²+4*x*sin(x))dx

# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt

def f(x):
  return x**2 + 4*x*np.sin(x) 
def intf(x): 
  return x**3/3.0+4.0*np.sin(x) - 4.0*x*np.cos(x)
a = 2;  
b = 3; 
# use N draws 
N= 10000
X = np.random.uniform(low=a, high=b, size=N) # N values uniformly drawn from a to b 
Y =f(X)  # CALCULATE THE f(x) 
# 蒙特卡洛法计算定积分：面积=宽度*平均高度
Imc= (b-a) * np.sum(Y)/ N;
exactval=intf(b)-intf(a)
print "Monte Carlo estimation=",Imc, "Exact number=", intf(b)-intf(a)
# --How does the accuracy depends on the number of points(samples)? Lets try the same 1-D integral 
# The Monte Carlo methods yield approximate answers whose accuracy depends on the number of draws.
Imc=np.zeros(1000)
Na = np.linspace(0,1000,1000)
exactval= intf(b)-intf(a)
for N in np.arange(0,1000):
  X = np.random.uniform(low=a, high=b, size=N) # N values uniformly drawn from a to b 
  Y =f(X)  # CALCULATE THE f(x) 
  Imc[N]= (b-a) * np.sum(Y)/ N;   
plt.plot(Na[10:],np.sqrt((Imc[10:]-exactval)**2), alpha=0.7)
plt.plot(Na[10:], 1/np.sqrt(Na[10:]), 'r')
plt.xlabel("N")
plt.ylabel("sqrt((Imc-ExactValue)$^2$)")
plt.show()

>>>

Estimation Monte Carlo= 11.8181144118 Nombre exact= 11.8113589251

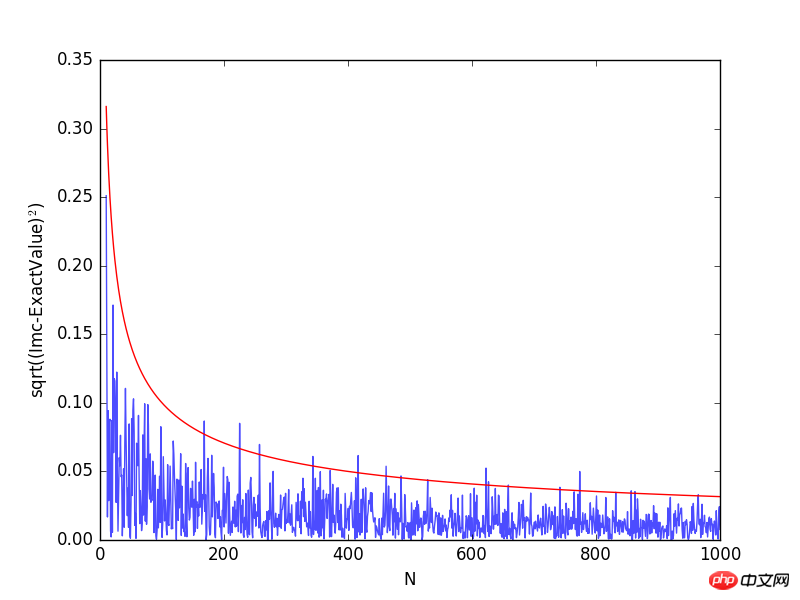
Comme le montre la figure ci-dessus, à mesure que le nombre de points d'échantillonnage augmente, l'erreur de calcul diminue progressivement. Il existe deux manières d'améliorer la précision des résultats de simulation : l'une consiste à augmenter le nombre de tests N ; l'autre consiste à réduire la variance σ2. L'augmentation du nombre de tests augmentera inévitablement le temps total de calcul utilisé pour résoudre le problème In. afin d'améliorer la précision, le but est évidemment inapproprié. Ensuite, nous présenterons la méthode d'échantillonnage importante pour réduire la variance et améliorer la précision du calcul intégral.

La caractéristique de la méthode d'échantillonnage par importance est qu'elle n'échantillonne pas à partir de la distribution de probabilité d'un processus donné, mais des échantillons à partir d'une distribution de probabilité modifiée, de sorte que les événements importants pour les résultats de la simulation apparaissent plus fréquemment, améliorant ainsi l'efficacité de l'échantillonnage, réduisant ainsi le temps de calcul consacré aux événements qui sont insignifiants pour les résultats de la simulation. Par exemple, trouvez l'intégrale de g(x) sur l'intervalle [a b]. Si un échantillonnage uniforme est utilisé, le nombre de points d'échantillonnage générés dans l'intervalle où la valeur de la fonction g(x) est relativement petite est le même que le nombre. de points d'échantillonnage générés dans l'intervalle où la valeur de la fonction est grande. Fermer, évidemment l'efficacité d'échantillonnage n'est pas élevée. Vous pouvez changer la fonction de densité de probabilité d'échantillonnage en f(x), de sorte que les formes de f(x) et g(. x) sont similaires, ce qui peut garantir que les chances d'échantillonnage des valeurs qui contribuent grandement au calcul intégral soient supérieures à la valeur d'échantillonnage avec une faible contribution, c'est-à-dire que l'opération intégrale peut être réécrite comme :

<.>

x est une variable aléatoire obtenue par échantillonnage selon la densité de probabilité f(x), évidemment dans l'intervalle [a b ] doit contenir :

Par conséquent, la valeur intégrale I peut être facilement considérée comme l'espérance de la variable aléatoire Y = g(x)/f(x), dans la formule xi est un point d'échantillonnage soumis à la densité de probabilité f(x)

L'exemple suivant utilise une fonction de distribution normale f(x) pour approximer g(x)=sin(x ) * 🎜>

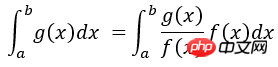
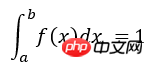
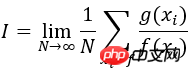
On peut voir sur la figure que la forme de la courbe sin(x)*x est similaire à la forme de la courbe de distribution normale, donc le nombre de points d'échantillonnage au sommet de la courbe sera plus grand que cela de la courbe Il y a plus de places dans les endroits inférieurs. Le résultat du calcul précis est pi. Comme le montre l'image de droite ci-dessus : les deux méthodes calculent l'intégrale définie 1000 fois. Les résultats proches de la valeur précise pi = 3,1415 sont les plus éloignés de la valeur précise. plus le nombre est petit, cela est évidemment conforme au chiffre conventionnel. Cependant, la différence au carré de la valeur intégrale calculée selon la méthode traditionnelle (histogramme rouge) est nettement plus grande que celle obtenue avec la méthode d'échantillonnage importante (histogramme bleu). Par conséquent, l’utilisation de la méthode d’échantillonnage par importance pour calculer peut réduire la variance et améliorer la précision. De plus, il convient de noter que le choix de la fonction f(x) affectera la précision des résultats du calcul. Lorsque la fonction f(x) que nous choisissons est très différente de g(x), la variance des résultats du calcul sera importante. augmentent également.

# -*- coding: utf-8 -*-
# Example: Calculate ∫sin(x)xdx

# The function has a shape that is similar to Gaussian and therefore
# we choose here a Gaussian as importance sampling distribution.
from scipy import stats
from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt
mu = 2;
sig =.7;
f = lambda x: np.sin(x)*x
infun = lambda x: np.sin(x)-x*np.cos(x)
p = lambda x: (1/np.sqrt(2*np.pi*sig**2))*np.exp(-(x-mu)**2/(2.0*sig**2))
normfun = lambda x: norm.cdf(x-mu, scale=sig)

plt.figure(figsize=(18,8)) # set the figure size
# range of integration
xmax =np.pi 
xmin =0
# Number of draws 
N =1000
# Just want to plot the function
x=np.linspace(xmin, xmax, 1000)
plt.subplot(1,2,1)
plt.plot(x, f(x), 'b', label=u'Original $x\sin(x)$')
plt.plot(x, p(x), 'r', label=u'Importance Sampling Function: Normal')
plt.xlabel('x')
plt.legend()
# =============================================
# EXACT SOLUTION 
# =============================================
Iexact = infun(xmax)-infun(xmin)
print Iexact
# ============================================
# VANILLA MONTE CARLO 
# ============================================
Ivmc = np.zeros(1000)
for k in np.arange(0,1000):
  x = np.random.uniform(low=xmin, high=xmax, size=N)
  Ivmc[k] = (xmax-xmin)*np.mean(f(x))
# ============================================
# IMPORTANCE SAMPLING 
# ============================================
# CHOOSE Gaussian so it similar to the original functions

# Importance sampling: choose the random points so that
# more points are chosen around the peak, less where the integrand is small.
Iis = np.zeros(1000)
for k in np.arange(0,1000):
  # DRAW FROM THE GAUSSIAN: xis~N(mu,sig^2)
  xis = mu + sig*np.random.randn(N,1);
  xis = xis[ (xis<xmax) & (xis>xmin)] ;
  # normalization for gaussian from 0..pi
  normal = normfun(np.pi)-normfun(0)   # 注意:概率密度函数在采样区间[0 pi]上的积分需要等于1
  Iis[k] =np.mean(f(xis)/p(xis))*normal  # 因此,此处需要乘一个系数即p(x)在[0 pi]上的积分
plt.subplot(1,2,2)
plt.hist(Iis,30, histtype=&#39;step&#39;, label=u&#39;Importance Sampling&#39;);
plt.hist(Ivmc, 30, color=&#39;r&#39;,histtype=&#39;step&#39;, label=u&#39;Vanilla MC&#39;);
plt.vlines(np.pi, 0, 100, color=&#39;g&#39;, linestyle=&#39;dashed&#39;)
plt.legend()
plt.show()

Recommandations associées :

Comment utiliser NotImplementedError dans Python programmation_python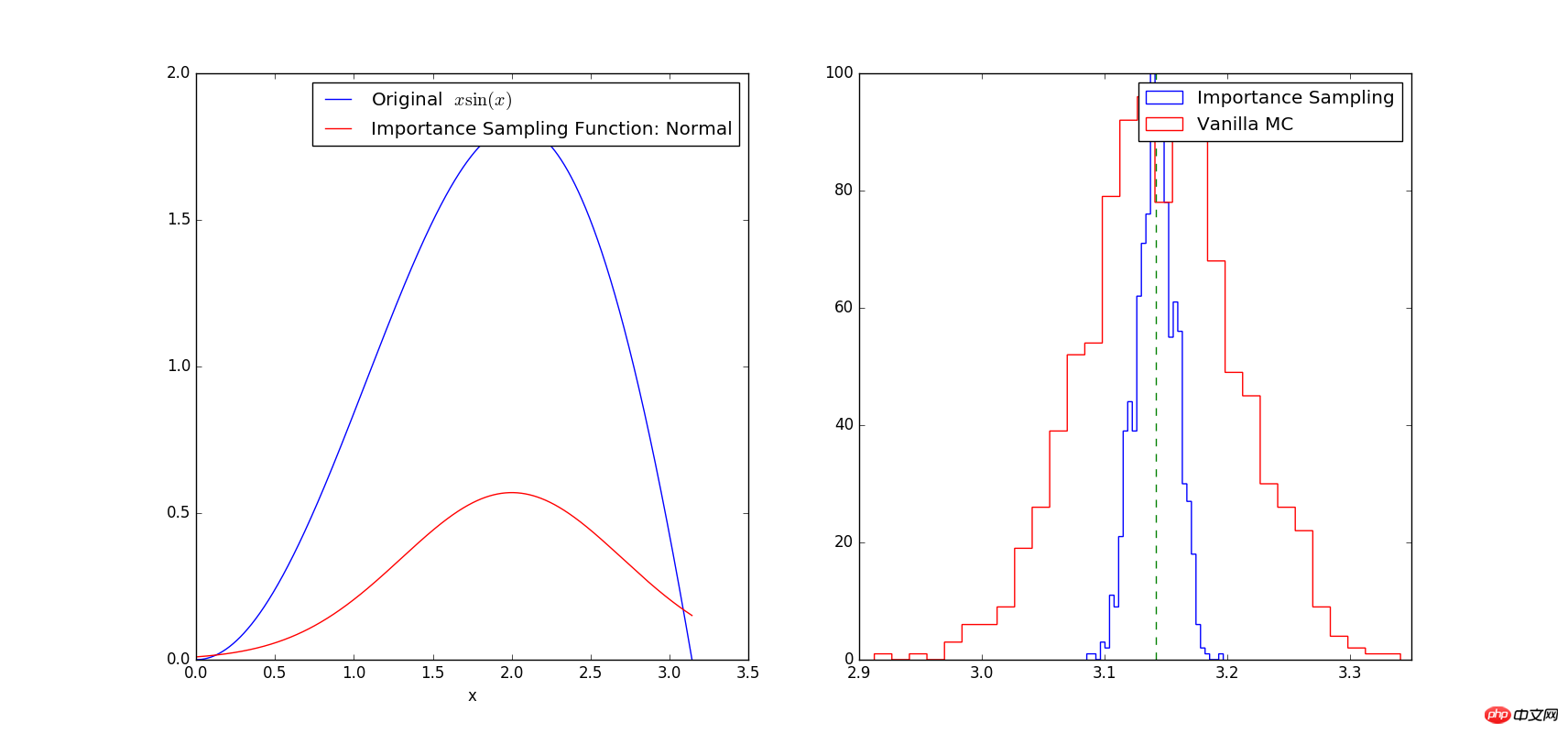

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!