Traitement morphologique avancé du traitement d'images numériques Python

Cet article présente principalement le traitement morphologique avancé du traitement d'images numériques python. Maintenant, je le partage avec vous et le donne comme référence. Jetons un coup d'oeil ensemble

Le traitement morphologique, en plus des opérations les plus élémentaires d'expansion, de corrosion, d'ouverture/fermeture, de traitement du chapeau noir/blanc, il existe également des applications plus avancées, telles que la coque convexe, la région connectée marquage, suppression de petites zones, etc.

1. Coque convexe

La coque convexe fait référence à un polygone convexe qui contient tous les pixels blancs de l'image. La fonction

est :

skimage.morphology.convex_hull_image(image)

L'entrée est une image binaire et la sortie est une image binaire logique. Les points à l'intérieur de la coque convexe sont vrais, sinon faux

Exemple :

import matplotlib.pyplot as plt
from skimage import data,color,morphology

#生成二值测试图像
img=color.rgb2gray(data.horse())
img=(img<0.5)*1

chull = morphology.convex_hull_image(img)

#绘制轮廓
fig, axes = plt.subplots(1,2,figsize=(8,8))
ax0, ax1= axes.ravel()
ax0.imshow(img,plt.cm.gray)
ax0.set_title(&#39;original image&#39;)

ax1.imshow(chull,plt.cm.gray)
ax1.set_title(&#39;convex_hull image&#39;)

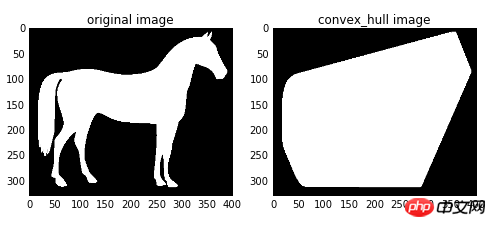
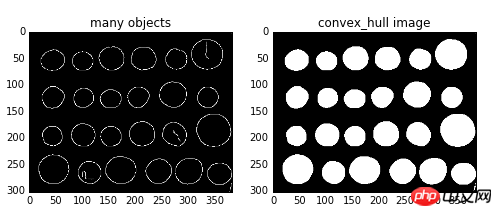
convex_hull_image( ) traite toutes les cibles de l'image dans leur ensemble, donc un seul polygone convexe minimum est calculé. S'il y a plusieurs objets cibles dans l'image et que chaque objet doit calculer un polygone convexe minimum, vous devez utiliser la fonction convex_hull_object().

Format de la fonction : skimage.morphology.convex_hull_object(image,neighbors=8 )

L'image du paramètre d'entrée est une image binaire, et les voisins indiquent s'il faut utiliser 4 connectés ou 8 connectés. La valeur par défaut est 8 connectés.

Exemple :

import matplotlib.pyplot as plt
from skimage import data,color,morphology,feature

#生成二值测试图像
img=color.rgb2gray(data.coins())
#检测canny边缘,得到二值图片
edgs=feature.canny(img, sigma=3, low_threshold=10, high_threshold=50) 

chull = morphology.convex_hull_object(edgs)

#绘制轮廓
fig, axes = plt.subplots(1,2,figsize=(8,8))
ax0, ax1= axes.ravel()
ax0.imshow(edgs,plt.cm.gray)
ax0.set_title('many objects')
ax1.imshow(chull,plt.cm.gray)
ax1.set_title('convex_hull image')
plt.show()

2. Marque de zone connectée

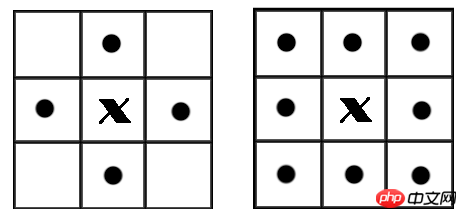
Dans une image binaire, si deux pixels sont adjacents et ont la même valeur (tous deux 0 ou 1), alors les deux pixels sont considérés comme étant dans une zone connexe. Tous les pixels de la même zone connectée sont marqués avec la même valeur. Ce processus est appelé marquage de zone connectée. Pour juger si deux pixels sont adjacents, nous utilisons généralement un jugement à 4 ou 8 connexions. Dans une image, la plus petite unité est un pixel, et chaque pixel est entouré de 8 pixels adjacents. Il existe deux relations de contiguïté courantes : 4-contiguïté et 8-contiguïté. 4 est adjacent à un total de 4 points, à savoir haut, bas, gauche et droite, comme le montre l'image de gauche ci-dessous. 8 Il y a 8 points adjacents au total, y compris les points situés en diagonale, comme le montre la figure de droite ci-dessous.

Dans le package skimage, nous utilisons la fonction label() sous le sous-module mesure pour implémenter l'étiquetage des zones connectées.

Format de la fonction :

skimage.measure.label（image,connectivity=None)

L'image dans le paramètre représente l'image binaire qui doit être traitée, et la connectivité représente la connexion mode, 1 représente 4 contiguïtés, 2 représente 8 contiguïtés.

Sort un tableau d'étiquettes (étiquettes), en commençant par 0.

import numpy as np
import scipy.ndimage as ndi
from skimage import measure,color
import matplotlib.pyplot as plt

#编写一个函数来生成原始二值图像
def microstructure(l=256):
  n = 5
  x, y = np.ogrid[0:l, 0:l] #生成网络
  mask = np.zeros((l, l))
  generator = np.random.RandomState(1) #随机数种子
  points = l * generator.rand(2, n**2)
  mask[(points[0]).astype(np.int), (points[1]).astype(np.int)] = 1
  mask = ndi.gaussian_filter(mask, sigma=l/(4.*n)) #高斯滤波
  return mask > mask.mean()

data = microstructure(l=128)*1 #生成测试图片

labels=measure.label(data,connectivity=2) #8连通区域标记
dst=color.label2rgb(labels) #根据不同的标记显示不同的颜色
print('regions number:',labels.max()+1) #显示连通区域块数(从0开始标记)

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4))
ax1.imshow(data, plt.cm.gray, interpolation='nearest')
ax1.axis('off')
ax2.imshow(dst,interpolation='nearest')
ax2.axis('off')

fig.tight_layout()
plt.show()

Dans le code, en multipliant par 1 à certains endroits, le tableau bool peut être rapidement converti en un tableau int.

Le résultat est tel qu'indiqué sur la figure : il y a 10 zones connectées, marquées de 0 à 9

Si vous souhaitez opérer sur chaque zone connectée séparément , comme la zone de calcul, le rectangle circonscrit, la zone de coque convexe, etc., vous devez appeler la fonction regionprops() du sous-module de mesure. Le format de cette fonction est :

skimage.measure.regionprops(label_image)

Renvoie la liste d'attributs de tous les blocs connectés. La liste d'attributs couramment utilisée est la suivante :

<.>

3、删除小块区域

有些时候，我们只需要一些大块区域，那些零散的、小块的区域，我们就需要删除掉，则可以使用morphology子模块的remove_small_objects（)函数。

函数格式：skimage.morphology.remove_small_objects(ar,min_size=64,connectivity=1,in_place=False)

参数：

ar: 待操作的bool型数组。

min_size: 最小连通区域尺寸，小于该尺寸的都将被删除。默认为64.

connectivity: 邻接模式，1表示4邻接，2表示8邻接

in_place: bool型值，如果为True,表示直接在输入图像中删除小块区域，否则进行复制后再删除。默认为False.

返回删除了小块区域的二值图像。

import numpy as np
import scipy.ndimage as ndi
from skimage import morphology
import matplotlib.pyplot as plt

#编写一个函数来生成原始二值图像
def microstructure(l=256):
  n = 5
  x, y = np.ogrid[0:l, 0:l] #生成网络
  mask = np.zeros((l, l))
  generator = np.random.RandomState(1) #随机数种子
  points = l * generator.rand(2, n**2)
  mask[(points[0]).astype(np.int), (points[1]).astype(np.int)] = 1
  mask = ndi.gaussian_filter(mask, sigma=l/(4.*n)) #高斯滤波
  return mask > mask.mean()

data = microstructure(l=128) #生成测试图片

dst=morphology.remove_small_objects(data,min_size=300,connectivity=1)

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4))
ax1.imshow(data, plt.cm.gray, interpolation='nearest')
ax2.imshow(dst,plt.cm.gray,interpolation='nearest')

fig.tight_layout()
plt.show()

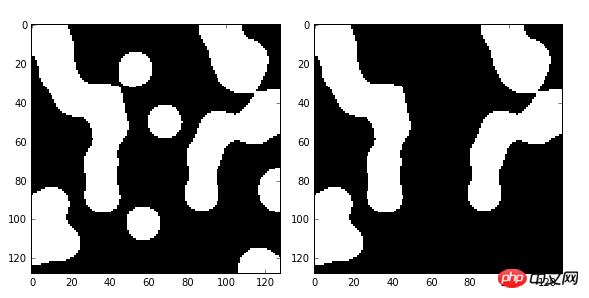
在此例中，我们将面积小于300的小块区域删除（由1变为0），结果如下图：

4、综合示例：阈值分割+闭运算+连通区域标记+删除小区块+分色显示

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
from skimage import data,filter,segmentation,measure,morphology,color

#加载并裁剪硬币图片
image = data.coins()[50:-50, 50:-50]

thresh =filter.threshold_otsu(image) #阈值分割
bw =morphology.closing(image > thresh, morphology.square(3)) #闭运算

cleared = bw.copy() #复制
segmentation.clear_border(cleared) #清除与边界相连的目标物

label_image =measure.label(cleared) #连通区域标记
borders = np.logical_xor(bw, cleared) #异或
label_image[borders] = -1
image_label_overlay =color.label2rgb(label_image, image=image) #不同标记用不同颜色显示

fig,(ax0,ax1)= plt.subplots(1,2, figsize=(8, 6))
ax0.imshow(cleared,plt.cm.gray)
ax1.imshow(image_label_overlay)

for region in measure.regionprops(label_image): #循环得到每一个连通区域属性集
  
  #忽略小区域
  if region.area < 100:
    continue

  #绘制外包矩形
  minr, minc, maxr, maxc = region.bbox
  rect = mpatches.Rectangle((minc, minr), maxc - minc, maxr - minr,
               fill=False, edgecolor=&#39;red&#39;, linewidth=2)
  ax1.add_patch(rect)
fig.tight_layout()
plt.show()

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!