Algorithme de tri PHP Shell Sort (Shell Sort)

Cet article présente principalement l'algorithme de tri PHP Shell Sort. Il analyse en détail les principes, les méthodes de mise en œuvre et les précautions associées sous forme d'exemples. Les amis dans le besoin peuvent s'y référer

L'exemple. dans cet article décrit l'algorithme de tri PHP Shell Sort. Partagez-le avec tout le monde pour référence, les détails sont les suivants :

Idée de base :

Le tri en colline signifie que les enregistrements sont regroupés par un certain incrément de l'indice, utilisez le tri par insertion directe pour chaque groupe. À mesure que l'incrément diminue progressivement, chaque groupe contient de plus en plus de mots-clés. Lorsque l'incrément diminue jusqu'à 1, la séquence entière est divisée en un groupe et l'algorithme se termine.

Étapes de l'opération :

Prenez d'abord un entier d1 inférieur à n (le nombre d'enregistrements de séquence) comme premier incrément, et ajoutez le Tous les enregistrements sont regroupés. Tous les enregistrements dont la distance est un multiple de d1 sont placés dans le même groupe. Effectuez d’abord le tri par insertion directe dans chaque groupe ; puis prenez le deuxième incrément d2 < d1 et répétez le regroupement et le tri ci-dessus jusqu’à ce que l’incrément dt=1( dt < d(t-1) ...< d2 < d1), c'est-à-dire jusqu'à ce que tous les enregistrements soient placés dans le même groupe pour le tri par insertion directe

Cette méthode est essentiellement une méthode d'insertion groupée

Comparaison des nombres qui. sont éloignés (appelés incréments) afin que les nombres puissent se déplacer sur plusieurs éléments, une seule comparaison[2] peut éliminer les échanges de plusieurs éléments. D.L. Shell a mis en œuvre cette idée en 1959 dans un algorithme de tri qui porte son nom. L'algorithme divise d'abord un ensemble de nombres à trier en plusieurs groupes selon un certain incrément d, et les indices enregistrés dans chaque groupe diffèrent de d. Trie tous les éléments de chaque groupe, puis utilise un incrément plus petit pour le trier. Triez à nouveau au sein de chaque groupe. Lorsque l'incrément diminue jusqu'à 1, le nombre entier à trier est divisé en un groupe et le tri est terminé.

Généralement, la moitié de la séquence est prise comme incrément pour la première fois, puis divisée par deux à chaque fois jusqu'à ce que l'incrément soit de 1.

Concernant la méthode de sélection des incréments, on dit que la meilleure séquence d'incréments n'a pas été trouvée jusqu'à présent, mais il existe une forte exigence selon laquelle la dernière valeur d'incrément doit être égale à 1.

Le processus de tri du shell pour une instance donnée

Supposons que le fichier à trier comporte 10 enregistrements et que les mots-clés sont :

49, 38, 65, 97, 76, 13, 27, 49, 55, 04.

Les valeurs de la séquence incrémentale sont :

5, 3, 1

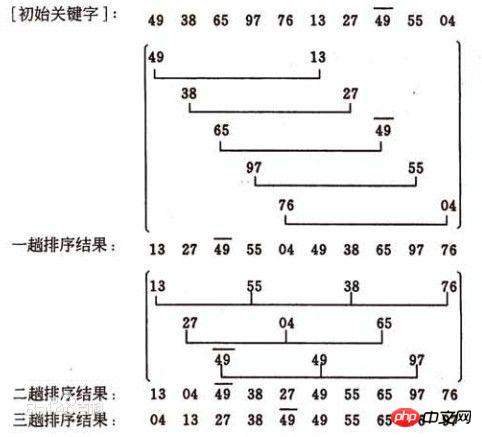
Implémentation de l'algorithme :

<?php
//希尔排序(对直接插入排序的改进)
function ShellSort(array &$arr)
{
  $count = count($arr);
  $inc = $count;  //增量
  do {
    //计算增量
    //$inc = floor($inc / 3) + 1;
    $inc = ceil($inc / 2);
    for ($i = $inc; $i < $count; $i++) {
      $temp = $arr[$i];  //设置哨兵
      //需将$temp插入有序增量子表
      for ($j = $i - $inc; $j >= 0 && $arr[$j + $inc] < $arr[$j]; $j -= $inc) {
        $arr[$j + $inc] = $arr[$j]; //记录后移
      }
      //插入
      $arr[$j + $inc] = $temp;
    }
    //增量为1时停止循环
  } while ($inc > 1);
}
//$arr = array(9,1,5,8,3,7,4,6,2);
$arr = array(49,38,65,97,76,13,27,49,55,04);
ShellSort($arr);
var_dump($arr);

Résultats en cours :

array(10) {
 [0]=>
 int(4)
 [1]=>
 int(13)
 [2]=>
 int(27)
 [3]=>
 int(38)
 [4]=>
 int(49)
 [5]=>
 int(49)
 [6]=>
 int(55)
 [7]=>
 int(65)
 [8]=>
 int(76)
 [9]=>
 int(97)
}

Analyse de complexité :

Grâce à l'analyse du code ci-dessus, je pense que tout le monde comprend dans une certaine mesure que la clé du tri Hill n'est pas de les regrouper au hasard et triez-les individuellement, mais les enregistrements séparés par un certain « incrément » sont formés en une sous-séquence pour obtenir un mouvement semblable à un saut, ce qui améliore l'efficacité du tri.

La complexité temporelle dans le pire des cas est O(n^2).

Le tri en colline est un tri instable.

Cet article est référencé à partir de "Dahua Data Structure". Il n'est enregistré ici que pour référence future.

Recommandations associées :

Partage d'exemples de tri par insertion de séries d'algorithmes de tri PHP

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!