Tour de Hanoï et séquence de Fibonacci implémentées en Python sur la base d'un algorithme récursif

Cet article présente principalement la Tour de Hanoï et la séquence de Fibonacci implémentée par Python sur la base de l'algorithme récursif. Il analyse les techniques d'implémentation récursives de la Tour de Hanoï et de la séquence de Fibonacci sous forme d'exemples. à cela

Cet article décrit les séquences de la Tour de Hanoï et de Fibonacci implémentées en Python sur la base d'algorithmes récursifs. Partagez-le avec tout le monde pour votre référence, les détails sont les suivants :

Ici, nous utilisons 2 exemples pour apprendre l'utilisation de la récursivité en python.

1. Trouvez le nombre d'indice n dans la séquence de Fibonacci (l'indice compte à partir de 0)

La forme de la séquence de Fibonacci est Comme ceci : 0,1,1,2,3,5,8,13...

① En utilisant la boucle while , le code python2 est le suivant :

def fib(n):
  a,b=0,1
  count=0
  while count<n:
    a,b=b,a+b
    count=count+1
  print a

Les résultats d'exécution sont les suivants :

>>> >0
> >> fib(1)
1
>>> fib(2)
1
>>> 🎜>2
> ;>> fib(4)
3
>>> Utilisez la récursivité (la récursion doit être des conditions aux limites)
, le code python2 est le suivant :

Les résultats en cours d'exécution sont les suivants :

def fib(n):
  if n==0 or n==1:#递归的边界条件
    return n
  else:
    return fib(n-1)+fib(n-2)

>>> fib(0)

0
>>> ;> fib(2)

1

>>> fib(3)

2

>>> >> fib(5)

5


La récursion est l'un des algorithmes qui exprime le mieux la pensée informatique. Prenons f(4) comme exemple et examinons le processus d'exécution de la récursivité. :




Le même programme utilise la récursion. Bien que le programme soit simple, l'efficacité d'exécution de la récursion est inférieure à celle de la boucle et la consommation des ressources du système est supérieure à celle de la boucle. boucle. Étant donné que la récursivité est appelée couche par couche, puis renvoyée couche par couche une fois terminée, l'efficacité d'exécution de la récursivité n'est pas élevée. Alors pourquoi utiliser la récursion ? En raison de certains problèmes, nous ne pouvons pas trouver de solution de boucle très évidente, mais il est facile de trouver une solution récursive évidente. Prenons par exemple le fameux problème de la Tour de Hanoï.

2. Tour de Hanoï

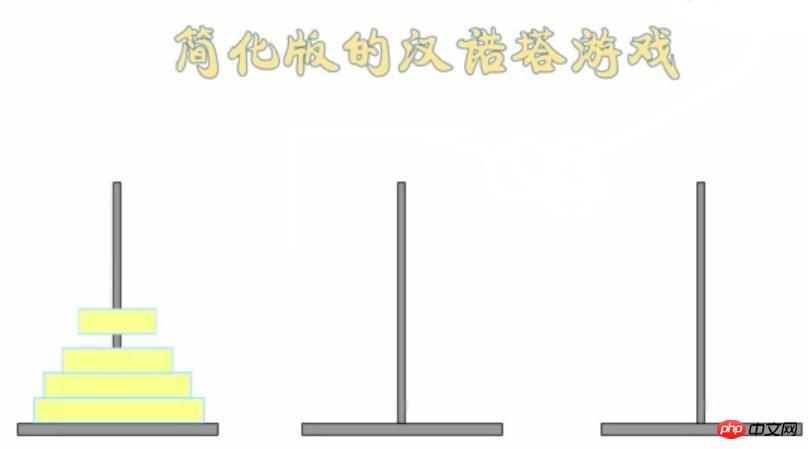
L'image ci-dessous est une version simplifiée du jeu Tour de Hanoï, avec seulement 4 planches :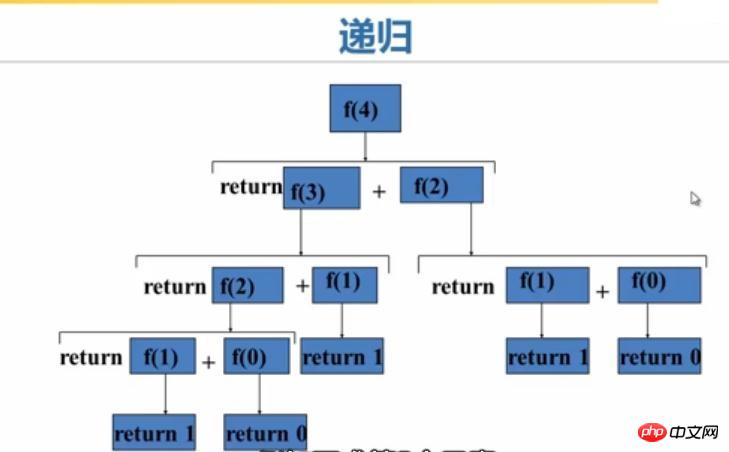

Les règles du jeu Tower of Hanoi sont les suivantes :

Le code python2 est le suivant :

Résultat de l'exécution :

>>> ','C',1)

A -> C
>>> hanoi('A','B','C',2)

A -> 🎜>A -> C

def hanoi(a,b,c,n):
  if n==1:#递归结束条件
    print a,'->',c
  else:
    hanoi(a,c,b,n-1)
    print a,'->',c
    hanoi(b,a,c,n-1)

B -> C

>>> hanoi('A','B','C',3)
A -> >A ->B

C ->B

A -> 🎜>

Recommandations associées :


Implémentation et application de l'algorithme de réseau neuronal (BP) Python

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!