Python teste si Jarque-Bera est conforme à la distribution normale

Le contenu de cet article est de tester si Jarque-Bera est conforme à la distribution normale en python. Il a une certaine valeur de référence. Les amis dans le besoin peuvent s'y référer

<.>La distribution normale est un test de normalité de la distribution d'une population. Lorsque la séquence obéit à la distribution normale, la statistique JB :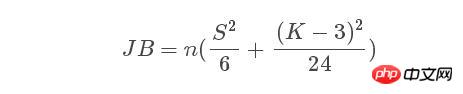

obéit asymptotiquement distribué. Où n est la taille de l'échantillon, S et K sont respectivement l'asymétrie et l'aplatissement de la variable aléatoire. La formule de calcul est la suivante :

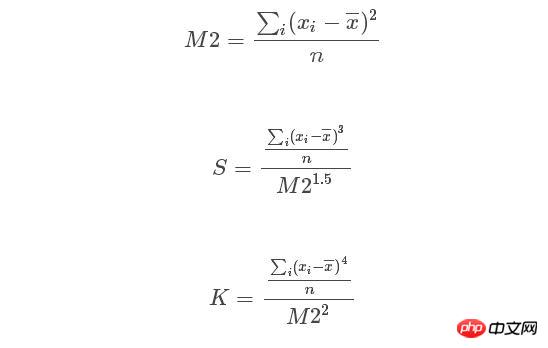
Les fonctions appelées pour l'asymétrie et l'aplatissement dans sicipy.stats de Python sont
et stats.skew(y), où la formule de l'aplatissement est stats.kurtosis(y)

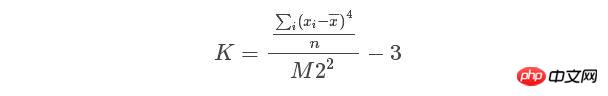
Dans Excel, la formule de calcul de l'asymétrie et de l'aplatissement est la suivante :

Implémentons les formules de calcul de l'asymétrie et de l'asymétrie dans la bibliothèque scipy de python et établissons un test de distribution normale.

Code

import numpy as npimport scipy.stats as statsdef self_JBtest(y):
    # 样本规模n
    n = y.size
    y_ = y - y.mean()    """
    M2:二阶中心钜
    skew 偏度 = 三阶中心矩 与 M2^1.5的比
    krut 峰值 = 四阶中心钜 与 M2^2 的比
    """
    M2 = np.mean(y_**2)
    skew =  np.mean(y_**3)/M2**1.5
    krut = np.mean(y_**4)/M2**2

    """
    计算JB统计量，以及建立假设检验
    """
    JB = n*(skew**2/6 + (krut-3 )**2/24)
    pvalue = 1 - stats.chi2.cdf(JB,df=2)
    print("偏度：",stats.skew(y),skew)
    print("峰值：",stats.kurtosis(y)+3,krut)
    print("JB检验：",stats.jarque_bera(y))    return np.array([JB,pvalue])

y1 = stats.norm.rvs(size=10)

y2 = stats.t.rvs(size=1000,df=4)

print(self_JBtest(y1))

print(self_JBtest(y2))

Résultat

=============== RESTART: C:\Users\tinysoft\Desktop\JB正态性检验.py =============== 

  偏度： 0.5383125387398069 0.53831253874 

  峰值： 2.9948926317585918 2.99489263176 

  JB检验： (0.48297818444514068, 0.78545737133644544) 

  [ 0.48297818  0.78545737] 

  偏度： -1.0488825341925703 -1.04888253419 

  峰值： 13.40804986639119 13.4080498664 

  JB检验： (4697.0050126426095, 0.0) 

  [ 4697.00501264     0.        ]

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!