Python implémente la méthode de résolution du plus grand diviseur commun

Cette fois, je vais vous amener Python pour implémenter la méthode de résolution du plus grand diviseur commun. Quelles sont les précautions pour que Python implémente la méthode de résolution du plus grand diviseur commun. Ce qui suit est un cas pratique. Jetons un coup d'œil.

Tout d'abord, extrayez une description de l'algorithme sur Internet comme suit :

Méthode de soustraction de phase supplémentaire : également appelée méthode de soustraction de phase de mise à jour, il s'agit d'une convention maximale de "Neuf chapitres d'arithmétique" Il s'agit d'un algorithme pour les nombres. Il a été conçu à l'origine pour la réduction, mais il convient à toute situation où il faut trouver le plus grand diviseur commun.

"Neuf chapitres sur l'arithmétique" est un ancien traité de mathématiques chinois. La "Technique de soustraction supplémentaire" qu'il contient peut être utilisée pour trouver le plus grand diviseur commun de deux nombres, c'est-à-dire ". celui qui peut être la moitié" Si la moitié n'est pas autorisée, le nombre du dénominateur et de l'enfant est substitué. Si le plus petit est inférieur au plus grand, le plus grand est réduit, il est donc égal à l'autre. "

Traduit en langage moderne comme suit :

Étape 1 : Étant donné deux entiers positifs ; Si oui, utilisez 2 pour réduire ; sinon, effectuez la deuxième étape.

Étape 2 : Soustrayez le plus petit nombre du plus grand nombre, puis comparez la différence résultante avec le plus petit nombre et réduisez le nombre du plus grand nombre. Continuez cette opération jusqu'à ce que le sous-trahend et la différence résultants soient égaux.

Après avoir lu la description ci-dessus, ma première réaction a été : y a-t-il quelque chose qui ne va pas avec cette description ? En termes d'universalité, il devrait y avoir des problèmes. Par exemple, si je trouve le plus grand diviseur commun de 4 et 4, mais après moitié-moitié, le résultat doit être faux ! L’algorithme suivant ne peut pas non plus être exécuté !

Quoi qu'il en soit, implémentons d'abord la description de l'algorithme ci-dessus :

# -*- coding:utf-8 -*-
#! python2
def MaxCommpisor(m,n):
  # even process
  while m % 2 == 0 and n % 2 == 0:
    m = m / 2
    n = n / 2
  # exchange order when needed
  if m < n:
    m,n = n,m
  # calculate the max comm pisor
  while m - n != n:
    diff = m - n
    if diff > n:
      m = diff
    else:
      m = n
      n = diff
  return n
print(MaxCommpisor(55,120))
print(MaxCommpisor(55,77))
print(MaxCommpisor(32,64))
print(MaxCommpisor(16,128))

Résultats d'exécution :

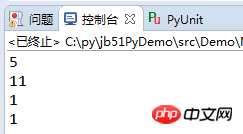
Inutile de dire que le programme ci-dessus L'exécution est truffée d'erreurs. Alors comment le corriger ?

Tout d'abord, toutes les divisions par 2 doivent être comptées à rebours à la fin ! De cette façon, le programme est modifié comme suit :

def MaxCommpisor(m,n):
  com_factor = 1
  if m == n:
    return n
  else:
    # process for even number
    while m % 2 == 0 and n % 2 == 0:
      m = int(m / 2)
      n = int(n / 2)
      com_factor *= 2
    if m < n:
      m,n = n,m
    diff = m - n
    while n != diff:
      m = diff
      if m < n:
        m,n = n,m
      diff = m - n
    return n * com_factor
print(MaxCommpisor(55,120))
print(MaxCommpisor(55,77))
print(MaxCommpisor(32,64))
print(MaxCommpisor(16,128))

Après modification, le résultat de l'exécution du programme ci-dessus est le suivant

Bien que cela Le programme semble un peu bizarre une fois écrit, mais l'algorithme global est toujours implémenté. Par rapport à des algorithmes tels que la division euclidienne, cette probabilité sera réduite dans une certaine mesure au niveau de la boucle . Surtout pour les deux dernières paires de numéros de test, l'effet est meilleur dans ce cas. Cependant, je ne suis pas encore en mesure de donner une mesure précise de l’efficacité globale de l’algorithme.

Je pense que vous maîtrisez la méthode après avoir lu le cas dans cet article. Pour des informations plus intéressantes, veuillez prêter attention aux autres articles connexes sur le site Web chinois de php. !

Lecture recommandée :

Résumé des compétences d'utilisation de Pycharm

Comment obtenir la valeur de crête locale d'un objet bidimensionnel tableau en python

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!