Maison >interface Web >js tutoriel >Comment créer une sous-séquence publique en JS
Comment créer une sous-séquence publique en JS
- php中世界最好的语言original
- 2018-03-23 13:40:501672parcourir
Cette fois, je vais vous montrer comment créer une sous-séquence publique en JS. Quelles sont les précautions pour implémenter une sous-séquence publique en JS. Voici un cas pratique, jetons un oeil.
Introduction
La sous-séquence commune la plus longue consiste à extraire tous les éléments possibles des deux séquences données X et Y. Les caractères supplémentaires possibles sont disposés dans l'ordre dans lequel ils sont disposés dans la séquence originale. L'algorithme pour les problèmes LCS a un large éventail d'utilisations. Par exemple, dans la gestion de différentes versions de logiciels, l'algorithme LCS est utilisé pour trouver les similitudes et les différences entre l'ancienne et la nouvelle version dans les tests de logiciels. utilisé pour comparer les séquences enregistrées et rejouées. Dans le domaine du génie génétique, l'algorithme LCS est utilisé. L'algorithme vérifie les similitudes et les différences entre le brin d'ADN du patient et le brin d'ADN de la liaison dans le système anti-plagiat, l'algorithme LCS est utilisé. utilisé pour vérifier le taux de plagiat du journal. L'algorithme LCS peut également être utilisé pour la mesure de similarité de code de programme, la récupération de séquences d'exécution humaine, la mise en correspondance de segments vidéo, etc., de sorte que la recherche sur l'algorithme LCS a une grande valeur d'application.
Sous-séquence : Une sous-séquence d'une séquence spécifique est une sous-séquence d'une séquence donnée Le résultat. obtenu en supprimant zéro ou plusieurs éléments (sans changer l'ordre relatif entre les éléments). Par exemple, les sous-séquences de la séquence Sous-séquence commune : Étant donné les séquences X et Y, la séquence Z est une sous-séquence de X et une sous-séquence de Y, alors Z est la sous-séquence commune de X et Y. Par exemple, X=[A,B,C,B,D,A,B], Y=[B,D,C,A,B,A[, alors la séquence Z=[B,C,A] est XEtY Sous - séquence commune de , Sa longueur est 3. Mais Z n'est pas la plus longue sous-séquence commune de X et Y, et les séquences [B, C, B, A] et [B, D, A, B] sont également les plus longues sous-séquences communes de X et Y, avec une longueur de 4 , et X et Y n'ont pas de sous-suite commune de longueur supérieure ou égale à 5. Pour les sous-séquences communes de la séquence [A, B, C] et de la séquence [E, F, G], il n'existe que la séquence vide []. Sous-séquence commune la plus longue : Étant donné les séquences X et Y, sélectionnez celle ou plusieurs ayant la plus longue longueur parmi toutes leurs sous-séquences communes. Donnez-moi une photo pour expliquer : On peut voir La sous-séquence est pas nécessairement continu, ce qui est continu c'est la sous-chaîne. Analyse du problème Nous commençons toujours l'analyse à partir d'une matrice et dérivons nous-mêmes l'équation de transition d'état. Tout d'abord, nous convertissons le problème en un concept suffisamment familier au front-end. Au lieu de l'appeler en série, il peut être considéré comme un tableau ou une chaîne. Pour simplifier les choses, supposons simplement que deux chaînes soient comparées. Nous nous concentrons sur le concept de "sous-séquence", qui peut en supprimer plusieurs ou zéro, ou la totalité. À ce stade, notre première sous-séquence est une chaîne vide (si notre séquence n’est pas une chaîne, nous pouvons toujours) ! C’est quelque chose auquel vous devez vraiment faire attention ! Beaucoup de gens ne peuvent tout simplement pas comprendre le tableau de « Introduction aux algorithmes », et il y a aussi de nombreux blogueurs qui ne prétendent pas comprendre. On compare toujours de gauche à droite, et bien sûr la première chaîne, car c'est la hauteur de la matrice, est placée verticalement. Supposons La solution de l'équation LCS est un nombre, ce tableau ne peut donc être rempli que de nombres. La longueur de la zone commune de deux chaînes vides est 0. Ensuite, nous élargissons un peu le problème. Cette fois, les deux côtés produisent un caractère. Évidemment, ce n'est que lorsque les deux sont identiques qu'il peut y avoir une sous-séquence commune qui n'est pas une chaîne vide, et la longueur peut également. être compris comme 1. Toute sous-séquence dans laquelle A est "X" et Y est "BDCA" Si Ensuite, regardons d'abord B, ${X_1} == ${Y_0}, nous obtenons une nouvelle sous-chaîne publique et nous devrions ajouter 1. Pourquoi? Parce que notre matrice est une table d'états, décrivant le processus de migration des états de gauche à droite et de haut en bas, et ces états sont accumulés sur la base des états existants. Ce que nous devons maintenant confirmer, c'est la relation entre la valeur de la grille que nous voulons remplir et les valeurs des grilles qui l'entourent et qui ont déjà été remplies. Pour l’instant, il y a trop peu d’informations et ce n’est qu’un point isolé. Il suffit de remplir 1. Ensuite, nous laissons Y avoir un D supplémentaire comme assistant, {"",A,B,AB} vs {"",B,D,BD} Évidemment, continuez à remplir 1. . Continuez à remplir Jusqu'au deuxième B de Y, tout est 1. Parce que lorsqu’il s’agit de BDCAB, ils ont une autre sous-séquence commune, AB. À ce stade, nous pouvons résumer quelques règles. Ensuite, nous vérifierons nos idées par des calculs et ajouterons de nouvelles règles ou contraintes pour les améliorer. Y envoie tous les caractères, X fait toujours 2 caractères, après observation attentive, remplissez toujours 2. Regardez les cinq lignes, envoyez plus X Si l’ensemble des sous-séquences de C et ABC est plus grand que l’ensemble des sous-séquences de AB, alors lui et l’ensemble des sous-séquences B de Y sont plus grands, même s’ils ne sont pas plus grands, ils ne peuvent pas être plus petits que les sous-séquences d’origine. Évidemment, le C nouvellement ajouté ne peut pas devenir une puissance de combat et n'est pas un caractère commun entre les deux, donc la valeur doit être égale à l'ensemble de sous-séquence de AB. Et nous pouvons être sûrs que si les caractères à comparer entre les deux chaînes sont différents, alors la grille à remplir est liée au côté gauche ou supérieur, et le côté le plus grand sera utilisé. Si les caractères comparés sont les mêmes, ne vous inquiétez pas, il arrive que le C de X doive être comparé au C de Y, c'est-à-dire l'ensemble de sous-séquences de ABC {"",A, B,C,AB,BC, ABC} est comparé à l'ensemble de sous-séquences {"",B,D,C,BD,DC,BDC} de BDC, et les sous-chaînes communes obtenues sont "",B,D. À ce stade, la conclusion est toujours la même qu'avant. Lorsque les caractères sont égaux, la valeur de la grille correspondante est égale à la valeur des coins gauche, droit et supérieur gauche, et les côtés gauche, supérieur et supérieur gauche sont. toujours égal. Ces mystères nécessitent des connaissances mathématiques plus rigoureuses pour être démontrés. Supposons qu'il y ait deux tableaux, A et B. A[i] est le i-ème élément de A, et A(i) est le préfixe constitué du premier élément du i-ème élément de A. m(i, j) est la plus longue longueur de sous-séquence commune de A(i) et B(j). En raison de la nature récursive de l'algorithme lui-même, en fait, il suffit de prouver que pour un certain i et j : m(i, j) = m(i- 1, j-1) + 1 (Quand A[i] = B[j]) m(i, j) = max( m(i-1, j), m(i, j- 1) ) (Quand A[ i] != B[j]) La première formule est facile à prouver, c'est-à-dire quand A[i] = B[j]. Vous pouvez utiliser une contre-preuve, en supposant que m(i, j) > m(i-1, j-1) + 1 (m(i, j) ne peut pas être inférieur à m(i-1, j-1) + 1, il y a plusieurs raisons évidemment), alors on peut en déduire le résultat contradictoire que m(i-1, j-1) n'est pas le plus long. Le second est un peu délicat. Lorsque A[i] != B[j], c'est toujours une réfutation, en supposant que m(i, j) > max( m(i-1, j), m(i, j-1) ). Par hypothèse de réfutation, nous pouvons obtenir m(i, j) > On peut en déduire que A[i] doit être dans la séquence LCS correspondant à m(i, j) (des preuves contradictoires sont disponibles). Et puisque A[i] != B[j], B[j] ne doit pas être dans la séquence LCS correspondant à m(i, j). On peut donc en déduire que m(i, j) = m(i, j-1). Cela conduit à des résultats qui contredisent de toute façon l’hypothèse. Obtenez une certification. Nous utilisons maintenant l'équation ci-dessous pour continuer à remplir le tableau. La mise en œuvre du programme LCS peut être encore simplifiée en déplaçant la position et en éliminant le besoin de générer de nouveaux tableaux Imprimer un LCS Nous allons donner la fonction d'impression et voir comment en imprimer un en premier. Nous commençons à regarder depuis le coin inférieur droit et terminons par la ligne supérieure. Par conséquent, la chaîne cible est construite dans l’ordre inverse. Afin d'éviter d'utiliser des quantités intermédiaires gênantes telles que stringBuffer, nous pouvons l'implémenter de manière récursive. Chaque fois que le programme est exécuté, une seule chaîne est renvoyée, sinon une chaîne vide est renvoyée, en utilisant printLCS(x,y,...) +. str[ i] sont ajoutés pour obtenir la chaîne dont nous avons besoin. Écrivons une autre méthode pour vérifier si la chaîne que nous obtenons est une vraie chaîne LCS. En tant que personne qui travaille déjà, je ne peux pas écrire de code comme un étudiant à l'école, sans faire des tests unitaires puis le mettre en ligne pour que d'autres puissent s'en servir. Utilisation : Imprimer tous les LCS L'idée est similaire à celle ci-dessus. Notons qu'il existe une valeur Math.max dans la méthode LCS. Celle-ci intègre en fait trois situations, donc trois chaînes peuvent être bifurquées. Notre méthode renverra un objet de collection es6 pour une suppression automatique. Puis à chaque fois le nouvel ensemble est utilisé pour fusionner les chaînes de l’ancien ensemble. Utilisation : Optimisation de l'espace Utilisation Tableau roulant : Solution récursive dangereuse Une sous-séquence de str1 correspond à la séquence d'indice {1, 2, … , a sous-séquence de m}. Par conséquent, str1 a un total de ${2^m}$ différentes sous-séquences (il en va de même pour str2, comme ${2^n}$), donc la complexité atteint un temps exponentiel étonnant ($ { 2^m * 2^n}$). Je pense que vous maîtrisez la méthode après avoir lu le cas dans cet article. Pour des informations plus intéressantes, veuillez prêter attention aux autres articles connexes sur le site Web chinois de php ! Lecture recommandée : Explication détaillée de l'utilisation du composant NavigatorIOS L'utilisation du modèle ejsExcel dans Vue.js Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Sous-chaîne : une nouvelle série formée en supprimant zéro ou plusieurs caractères du début, du dernier ou des deux d'une séquence. La différence est que les sous-séquences peuvent avoir des caractères coupés au milieu. Combien de séquences de neutrons possède cette chaîne de cnblogs ? Évidemment il y en a 27, comme cb, cgs, etc. sont toutes des sous-séquences 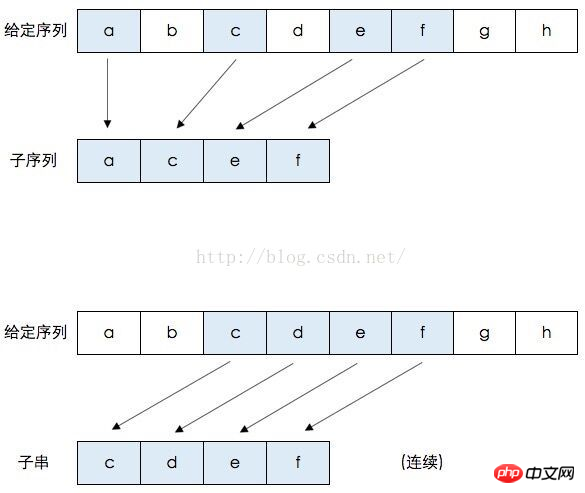
x "" B D C A B A "" A B C D A B x "" B D C A B A "" 0 A B C D A B x "" B D C A B A "" 0 0 0 0 0 0 0 A 0 B 0 C 0 D 0 A 0 B 0 x "" B D C A B A "" 0 0 0 0 0 0 0 A 0 0 0 0 1 B 0 C 0 D 0 A 0 B 0 x "" B D C A B A "" 0 0 0 0 0 0 0 A 0 0 0 0 1 1 1 B 0 1 C 0 D 0 A 0 B 0 x "" B D C A B A "" 0 0 0 0 0 0 0 A 0 0 0 0 1 1 1 B 0 1 1 1 1 2 C 0 D 0 A 0 B 0 
× "" B D C A B A "" 0 0 0 0 0 0 0 A 0 0 0 0 1 1 1 B 0 1 1 1 1 2 2 C 0 1 D 0 A 0 B 0 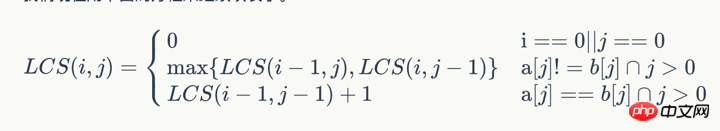
//by 司徒正美
function LCS(str1, str2){
var rows = str1.split("")
rows.unshift("")
var cols = str2.split("")
cols.unshift("")
var m = rows.length
var n = cols.length
var dp = []
for(var i = 0; i < m; i++){
dp[i] = []
for(var j = 0; j < n; j++){
if(i === 0 || j === 0){
dp[i][j] = 0
continue
}
if(rows[i] === cols[j]){
dp[i][j] = dp[i-1][j-1] + 1 //对角+1
}else{
dp[i][j] = Math.max( dp[i-1][j], dp[i][j-1]) //对左边,上边取最大
}
}
console.log(dp[i].join(""))//调试
}
return dp[i-1][j-1]
}//by司徒正美
function LCS(str1, str2){
var m = str1.length
var n = str2.length
var dp = [new Array(n+1).fill(0)] //第一行全是0
for(var i = 1; i <= m; i++){ //一共有m+1行
dp[i] = [0] //第一列全是0
for(var j = 1; j <= n; j++){//一共有n+1列
if(str1[i-1] === str2[j-1]){
//注意这里,str1的第一个字符是在第二列中,因此要减1,str2同理
dp[i][j] = dp[i-1][j-1] + 1 //对角+1
} else {
dp[i][j] = Math.max( dp[i-1][j], dp[i][j-1])
}
}
}
return dp[m][n];
}//by 司徒正美,打印一个LCS
function printLCS(dp, str1, str2, i, j){
if (i == 0 || j == 0){
return "";
}
if( str1[i-1] == str2[j-1] ){
return printLCS(dp, str1, str2, i-1, j-1) + str1[i-1];
}else{
if (dp[i][j-1] > dp[i-1][j]){
return printLCS(dp, str1, str2, i, j-1);
}else{
return printLCS(dp, str1, str2, i-1, j);
}
}
}
//by司徒正美, 将目标字符串转换成正则,验证是否为之前两个字符串的LCS
function validateLCS(el, str1, str2){
var re = new RegExp( el.split("").join(".*") )
console.log(el, re.test(str1),re.test(str2))
return re.test(str1) && re.test(str2)
}
function LCS(str1, str2){
var m = str1.length
var n = str2.length
//....略,自行补充
var s = printLCS(dp, str1, str2, m, n)
validateLCS(s, str1, str2)
return dp[m][n]
}
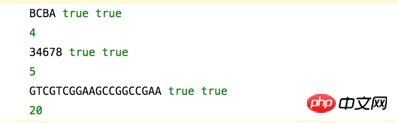
var c1 = LCS( "ABCBDAB","BDCABA");
console.log(c1) //4 BCBA、BCAB、BDAB
var c2 = LCS("13456778" , "357486782" );
console.log(c2) //5 34678
var c3 = LCS("ACCGGTCGAGTGCGCGGAAGCCGGCCGAA" ,"GTCGTTCGGAATGCCGTTGCTCTGTAAA" );
console.log(c3) //20 GTCGTCGGAAGCCGGCCGAA
//by 司徒正美 打印所有LCS
function printAllLCS(dp, str1, str2, i, j){
if (i == 0 || j == 0){
return new Set([""])
}else if(str1[i-1] == str2[j-1]){
var newSet = new Set()
printAllLCS(dp, str1, str2, i-1, j-1).forEach(function(el){
newSet.add(el + str1[i-1])
})
return newSet
}else{
var set = new Set()
if (dp[i][j-1] >= dp[i-1][j]){
printAllLCS(dp, str1, str2, i, j-1).forEach(function(el){
set.add(el)
})
}
if (dp[i-1][j] >= dp[i][j-1]){//必须用>=,不能简单一个else搞定
printAllLCS(dp, str1, str2, i-1, j).forEach(function(el){
set.add(el)
})
}
return set
}
}
function LCS(str1, str2){
var m = str1.length
var n = str2.length
//....略,自行补充
var s = printAllLCS(dp, str1, str2, m, n)
console.log(s)
s.forEach(function(el){
validateLCS(el,str1, str2)
console.log("输出LCS",el)
})
return dp[m][n]
}
var c1 = LCS( "ABCBDAB","BDCABA");
console.log(c1) //4 BCBA、BCAB、BDAB
var c2 = LCS("13456778" , "357486782" );
console.log(c2) //5 34678
var c3 = LCS("ACCGGTCGAGTGCGCGGAAGCCGGCCGAA" ,"GTCGTTCGGAATGCCGTTGCTCTGTAAA" );
console.log(c3) //20 GTCGTCGGAAGCCGGCCGAA

function LCS(str1, str2){
var m = str1.length
var n = str2.length
var dp = [new Array(n+1).fill(0)],now = 1,row //第一行全是0
for(var i = 1; i <= m; i++){ //一共有2行
row = dp[now] = [0] //第一列全是0
for(var j = 1; j <= n; j++){//一共有n+1列
if(str1[i-1] === str2[j-1]){
//注意这里,str1的第一个字符是在第二列中,因此要减1,str2同理
dp[now][j] = dp[i-now][j-1] + 1 //对角+1
} else {
dp[now][j] = Math.max( dp[i-now][j], dp[now][j-1])
}
}
now = 1- now; //1-1=>0;1-0=>1; 1-1=>0 ...
}
return row ? row[n]: 0
}
//警告,字符串的长度一大就会爆栈
function LCS(str1, str2, a, b) {
if(a === void 0){
a = str1.length - 1
}
if(b === void 0){
b = str2.length - 1
}
if(a == -1 || b == -1){
return 0
}
if(str1[a] == str2[b]) {
return LCS(str1, str2, a-1, b-1)+1;
}
if(str1[a] != str2[b]) {
var x = LCS(str1, str2, a, b-1)
var y = LCS(str1, str2, a-1, b)
return x >= y ? x : y
}
}
Articles Liés
Voir plus- Une analyse approfondie du composant de groupe de liste Bootstrap
- Explication détaillée du currying de la fonction JavaScript
- Exemple complet de génération de mot de passe JS et de détection de force (avec téléchargement du code source de démonstration)
- Angularjs intègre l'interface utilisateur WeChat (weui)
- Comment basculer rapidement entre le chinois traditionnel et le chinois simplifié avec JavaScript et l'astuce permettant aux sites Web de prendre en charge le basculement entre les compétences en chinois simplifié et traditionnel_javascript

