jQuery implémente la fonction de couche infinie récursive

Cette fois, je vais vous proposer jQuery pour implémenter la fonction de couche infinie récursive. Quelles sont les précautions à prendre pour jQuery pour implémenter la fonction de couche infinie récursive ? Ce qui suit est un cas pratique, jetons un coup d'oeil.

Chat

Il y a deux jours, un ami m'a dit qu'il voulait une fonction de recherche ztree, et je l'ai giflé : Ceci genre de chose Y a-t-il trop de méthodes que d'innombrables prédécesseurs n'ont pas réussi à appliquer ? Je suis allé le chercher moi-même, j'étais très occupé ~ Puis je me suis accroupi en silence et j'ai écrit la méthode de recherche pour zTree. Pourquoi? Parce que j'ai dit : « C'est impossible de le trouver. Il doit y avoir beaucoup de gens qui l'ont fait un nombre incalculable de fois. Si vous ne le trouvez pas, je vous l'écrirai et vous demanderai de déjeuner. pendant longtemps et je ne l'ai pas trouvé (les larmes, mon plan, mon déjeuner ~). La plupart d'entre eux utilisent getNodesByParamFuzzy() ou la mise en évidence dans l'API. Cependant, des amis ont dit que les exigences ne sont pas remplies : 1. Si la correspondance échoue, le nœud parent est également masqué 2. Les règles de correspondance peuvent être personnalisées, c'est-à-dire qu'elles peuvent faire correspondre les noms et les attributs... (Quoi qu'il en soit, qu'est-ce que c'est ? Je veux, ce n'est pas épicé, Xiaosheng Avec un sourire sur mon visage, mais dans mon cœur... alors je l'écrirai pour toi ~), entrez le texte ci-dessous :

Carte mentale

　

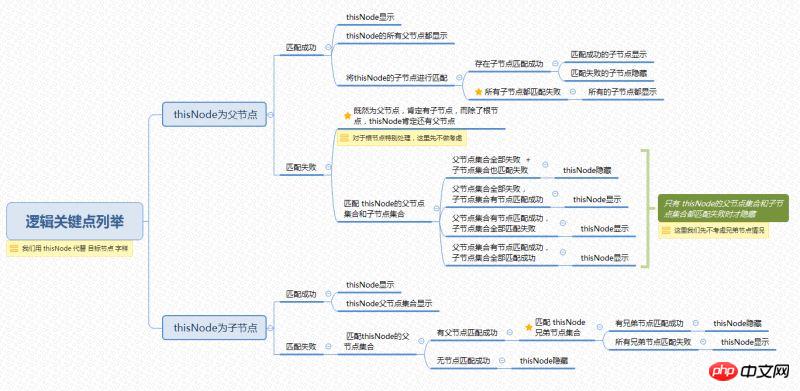
La fonction de recherche générale ne correspond qu'aux mots-clés dans la « plage établie (nom pratique) ». plage de recherche : par exemple, une bibliothèque de textes, une liste déroulante, en d'autres termes, la taille de notre ensemble d'objets correspondants a été déterminée. Cependant, cela n'est pas réalisable sur ztree. Pourquoi ? Quand j'ai réfléchi à la logique d'implémentation de la fonction de recherche ztree, j'ai demandé : alors, le niveau de cet arbre est-il fixe ? Ou vous ne savez pas combien de couches il y a ? Mon frère m'a regardé et a souri d'un air entendu : Vous écrivez en couches infinies ~ Le mollet de Xiaosheng a tremblé. . Parce que le niveau de l'arborescence est incertain, la plage de recherche est incertaine. Par exemple : le nœud cible correspond avec succès. Si ce nœud est un nœud enfant, alors son nœud parent doit également être affiché, puis le nœud parent de son nœud parent. être également affiché, puis le nœud parent du nœud parent de son nœud parent... Orz... Il semble que cela ne finira jamais... Il n'y a pas d'autre moyen que de : récurer pour trouver tous les nœuds parents et nœuds enfants du nœud cible.

Points clés de la logique

Dans la carte mentale ci-dessus, j'ai énuméré grossièrement la logique, dans quelles circonstances le nœud cible est affiché, et Quoi C'est un point clé sur lequel nous devons être clairs. Examinons de plus près l'existence du nœud cible : le développement de la fonction de recherche a été clairement compris dans l'esprit. La seule chose qui reste est la méthode de mise en œuvre. , ce n'est pas du tout un problème ~ (Xiaosheng pense secrètement que ce qui est vraiment inquiétant, c'est que le processus de la fonction n'est pas clair. Quant à la méthode d'implémentation, vous la connaissez tous. N'est-ce pas ? 0.0..)

À propos des nœuds d'arbre

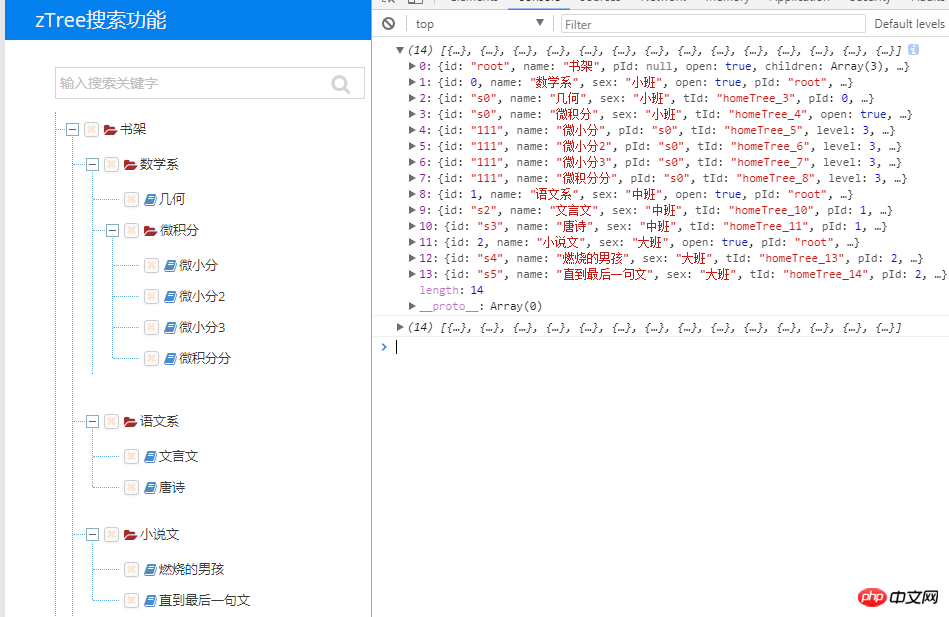
Pour compléter les différentes méthodes du processus ci-dessus, nous devons connaître une série d'attributs de nœuds d'arbre, nous savons tous qu'il existe un artefact comme l'API. Cependant, l'une des caractéristiques de l'API est qu'elle est complète (si complète que lorsque nous voulons trouver avec précision un certain attribut ou une certaine méthode, nous pouvons avoir du mal à chercher). Ce que nous voulons ici, c'est comment le faire. récupérons-nous rapidement Pour les attributs ou méthodes souhaités, nous imprimons le nœud d'arbre défini sur la console : En regardant l'image : nous pouvons voir tous les nœuds, y compris l'identifiant, le nom et d'autres attributs

 var treeObj=$.fn.zTree.getZTreeObj("homeTree"); // 设置根节点
  var node = treeObj.getNodes(); // 获取根节点
  var nodes = treeObj.transformToArray(node); // 获取所有节点
  console.log(nodes);

En regardant à nouveau l'image : nous pouvons voir divers attributs de n'importe quel nœud, y compris la collection de nœuds enfants que nous voulons, l'attribut du nœud parent isParent, l'identifiant du nœud tId, le parent node id parentTid.. .

Tout est prêt, commençons

Jetons un coup d'œil aux méthodes pertinentes De nombreux petits détails doivent être découverts au cours. le processus de codage réel. Ici, ils sont affichés pour plus de commodité. Répertoriez directement les méthodes.

Déclarez le tableau de sauvegarde :

Obtenez de manière récursive la collection de nœuds parents du nœud cible :

Obtenez de manière récursive la collection de nœuds enfants du nœud cible :

// 地区搜索
 var parentArray = [];
 var childArray = [];

Il est recommandé d'extraire la partie du nœud correspondant et d'écrire une méthode distincte pour faciliter l'expansion des règles de correspondance. Ici, nous supposons qu'en plus de faire correspondre le nom, nous devons également faire correspondre l'attributentity_code du nœud. :

 // 递归获取目标节点所有父节点
 function getParentsNode(treeNode){
  var thisParentNode = treeNode.getParentNode(); //得到该节点的父节点
  if( thisParentNode != null ){ // 父节点存在
   parentArray.push(thisParentNode); // 储存至数组
   getParentsNode(thisParentNode); // 重调 
  }else{
   return false;
  }   
 }

 //匹配节点
 function matchNode(treeNode,num){
  var inputArea = $("input[name='searchArea']");
  var name = treeNode.name;
  var entityCode = treeNode.entity_code|| '';
  var val = inputArea.val(); // 获取检索值
  var numName = name.indexOf(val);
  var numCode = entityCode.indexOf(val);
  var num = -1;
  if( numName != -1 || numCode !=-1 ){
   num = 1;
  }
  if( numName == -1 && numCode == -1 ){
   num = -1; 
  }
  return num;
 }

 　　节点匹配成功方法：

 // 节点匹配成功
 function checkTrueArray(arr,treeNode){
  var thisTid = treeNode.tId;
  var thisLi = $("#"+thisTid);
  for(var n=0;n<arr.length;n++){
   var thisNodeId = arr[n].tId;
   var thisNodeLi = $("#"+thisNodeId);
   thisLi.show();
   thisNodeLi.show();
  }
 }

 　　节点匹配失败方法：

 // 节点匹配失败
 function checkFalseArray(arr,treeNode){
  var result = [];
  var result2 = [];
  var thisTid = treeNode.tId;
  var thisLi = $("#"+thisTid);
  var val = inputArea.val(); // 获取检索值
  var thisParent = treeNode.getParentNode(); // 获取目标节点父节点
  if( thisParent != null ){ // 有父节点
   var thisBrotherArr = treeNode.getParentNode().children; // 得到包含自身的兄弟数组
   for(var m=0;m<arr.length;m++){ // 匹配父节点
    var num = matchNode(arr[m]);
    if( num != -1 ){
     result.push(arr[m]);
    }
   }
   var resultLength = result.length;
   for( var m=0;m<thisBrotherArr.length;m++ ){ // 匹配兄弟节点
    var num = matchNode(thisBrotherArr[m]);
    if( num != -1 ){
     result2.push(thisBrotherArr[m]);
    }
   }
   var resultLength2 = result2.length;
   // 对于自身匹配失败的节点，要显示必须满足有父节点匹配成功，且兄弟级节点都匹配失败
   if( (resultLength == 0 && resultLength2 == 0) || resultLength2 != 0 ){
    thisLi.hide();
   }
   if( resultLength !=0 && resultLength2 == 0 ){
    thisLi.show();
   }
  }else{
   thisLi.hide();
  } 
 }

 　　 目标节点匹配失败 目标节点即有父节点又有子节点：

 // 目标节点匹配失败 目标节点即有父节点又有子节点
 function checkAllArray(arr,arr2,treeNode){
  var result = [];
  var result2 = [];
  var thisTid = treeNode.tId;
  var thisLi = $("#"+thisTid);
  var val = inputArea.val(); // 获取检索值
  for(var m=0;m<arr.length;m++){ // 匹配子节点或父节点
   var num = matchNode(arr[m]);
   if( num != -1 ){
    result.push(arr[m]); // 匹配成功储存至数组
   }
  }
  var resultLength = result.length; // 获取匹配成功后返回的数组长度
  for(var m=0;m<arr2.length;m++){ // 匹配子节点或父节点
   var num = matchNode(arr2[m]);
   if( num != -1 ){
    result2.push(arr2[m]); // 匹配成功储存至数组
   }
  }
  var resultLength2 = result2.length; // 获取匹配成功后返回的数组长度
  if( resultLength == 0 && resultLength2 == 0 ){ // 子节点和父节点都匹配失败
   thisLi.hide();
  }else{ 
   thisLi.show(); // 有一种匹配成功或都匹配成功
  }
 }

　　定义搜索方法：

 function searchArea(treeId, treeNode){ // 定义搜索方法
  var inputArea = $("input[name='searchArea']");
  var val = inputArea.val(); // 获取检索值
  var treeObj=$.fn.zTree.getZTreeObj("homeTree"); // 设置根节点
  var node = treeObj.getNodes(); // 获取根节点
  var nodes = treeObj.transformToArray(node); // 获取所有节点
  console.log(nodes);
  for(var i=0;i
　　调用搜索方法：
 // 调用搜索方法
 $(".searchAreaBtn").click(function(treeId, treeNode){
  searchArea(treeId, treeNode);
 });
 var inputArea = $("input[name='searchArea']");
 inputArea.keyup(function(treeId, treeNode,e){
  var e = event || window.event;
  var val = inputArea.val();
  if( e.keyCode == 13 || val == "" ){
   searchArea(treeId, treeNode);
  }
 });
 　　看效果（电脑ps出问题了，用美图秀秀拼的图~囧...）：

结语
　　理论上来说应该是能支持无限层的，最多试了四层，没有问题，没有做更多测试，有兴趣的看官可以试试，需要demo的可以留言，互相学习，一起进步，么么哒~

相信看了本文案例你已经掌握了方法，更多精彩请关注php中文网其它相关文章！
推荐阅读：
jQuery与vue做出拖动验证的验证码效果

$.ajax()怎样从服务器获取json数据

jQuery动态显示select下拉列表数据
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!