Comment résoudre le problème de la perte de précision numérique dans les astuces JavaScript_javascript

Cet article est divisé en trois parties

• Quelques problèmes typiques avec la perte de précision numérique JS
• La raison pour laquelle la précision numérique JS est perdue
• Solution (un objet, une fonction)

1. Quelques problèmes typiques de perte de précision numérique JS

1. Ajoutez deux nombres simples à virgule flottante

0.1 + 0.2 != 0.3 // true

Ce n'est vraiment pas un problème de Firebug, vous pouvez essayer d'utiliser alert (haha, je plaisante).

Regardez les résultats de l'opération Java

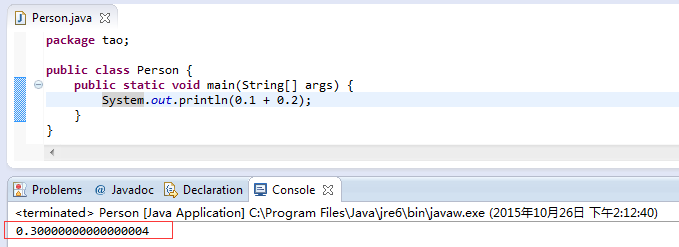
Regardez Python à nouveau

2. Opérations sur les grands entiers

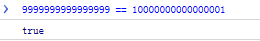
Cela n'a aucun sens que les nombres à 16 et 17 chiffres soient égaux.

Autre exemple

var x = 9007199254740992
x + 1 == x // ？

Voir les résultats

Trois vues ont de nouveau été renversées.

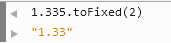
3. toFixed ne sera pas arrondi (Chrome)

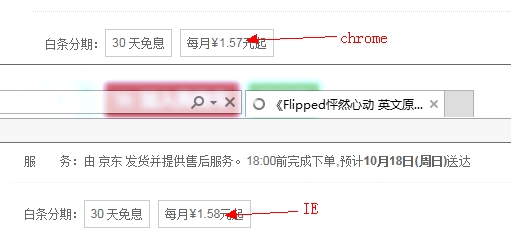
Il y a eu des cas en ligne où les prix dans Chrome n'étaient pas cohérents avec ceux d'autres navigateurs

2. Raisons pour lesquelles les nombres JS perdent en précision

L'implémentation binaire de l'ordinateur et la limite de bits limitent certains nombres qui ne peuvent pas être représentés de manière finie. Tout comme certains nombres irrationnels ne peuvent pas être représentés de manière finie, comme pi 3,1415926..., 1,3333... etc. JS suit la spécification IEEE 754, utilise un stockage double précision et occupe 64 bits. Comme le montre l'image

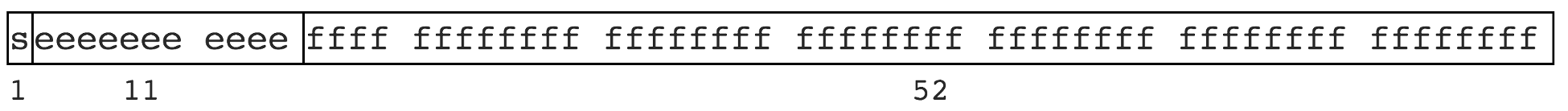
Signification

• 1 bit est utilisé pour représenter le bit de signe
• 11 bits sont utilisés pour représenter l'exposant
• 52 bits représentent la mantisse

Nombre à virgule flottante, tel que

0.1 >> 0.0001 1001 1001 1001…（1001无限循环）
0.2 >> 0.0011 0011 0011 0011…（0011无限循环）

À l'heure actuelle, nous ne pouvons imiter que le décimal pour l'arrondi, mais le binaire n'a que deux nombres : 0 et 1, il devient donc 0 et 1 pour l'arrondi. C'est la cause première des erreurs et de la perte de précision dans certaines opérations sur les nombres à virgule flottante dans les ordinateurs.

La perte de précision des grands entiers est essentiellement la même que celle des nombres à virgule flottante. Le nombre maximum de chiffres de mantisse est de 52. Par conséquent, le plus grand entier pouvant être représenté avec précision dans JS est Math.pow(2, 53) , qui en décimal est 9007199254740992.

Ceux plus grands que 9007199254740992 peuvent perdre en précision

9007199254740992  >> 10000000000000...000 // 共计 53 个 0
9007199254740992 + 1 >> 10000000000000...001 // 中间 52 个 0
9007199254740992 + 2 >> 10000000000000...010 // 中间 51 个 0

En fait

9007199254740992 + 1 // 丢失
9007199254740992 + 2 // 未丢失
9007199254740992 + 3 // 丢失
9007199254740992 + 4 // 未丢失

Le résultat est tel que montré sur l'image

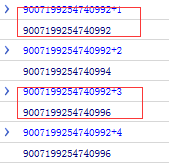
D'après ce qui précède, nous pouvons savoir que les nombres apparemment finis sont infinis dans la représentation binaire de l'ordinateur. En raison de la limitation du nombre de chiffres stockés, il y a un « arrondi » et une perte de précision se produit.

3. Solution

Pour les entiers, la probabilité de problèmes frontaux peut être relativement faible. Après tout, peu de besoins commerciaux nécessitent l'utilisation de très grands entiers tant que le résultat de l'opération ne dépasse pas Math.pow(2, 53), la précision ne sera pas perdue.

Pour les décimales, il existe encore de nombreuses chances de problèmes au niveau du front-end, surtout lorsque certains sites de commerce électronique impliquent des données telles que des montants. Solution : Mettez la décimale dans un entier (multipliez), puis réduisez-la au multiple d'origine (divisez le multiple)

// 0.1 + 0.2
(0.1*10 + 0.2*10) / 10 == 0.3 // true

Ce qui suit est un objet que j'ai écrit pour protéger la perte de précision dans les opérations décimales d'addition, de soustraction, de multiplication et de division. Bien entendu, l’entier converti ne peut toujours pas dépasser 9007199254740992.

/**
 * floatObj 包含加减乘除四个方法，能确保浮点数运算不丢失精度
 *
 * 我们知道计算机编程语言里浮点数计算会存在精度丢失问题（或称舍入误差），其根本原因是二进制和实现位数限制有些数无法有限表示
 * 以下是十进制小数对应的二进制表示
 *  0.1 >> 0.0001 1001 1001 1001…（1001无限循环）
 *  0.2 >> 0.0011 0011 0011 0011…（0011无限循环）
 * 计算机里每种数据类型的存储是一个有限宽度，比如 JavaScript 使用 64 位存储数字类型，因此超出的会舍去。舍去的部分就是精度丢失的部分。
 *
 * ** method **
 * add / subtract / multiply /divide
 *
 * ** explame **
 * 0.1 + 0.2 == 0.30000000000000004 （多了 0.00000000000004）
 * 0.2 + 0.4 == 0.6000000000000001 （多了 0.0000000000001）
 * 19.9 * 100 == 1989.9999999999998 （少了 0.0000000000002）
 *
 * floatObj.add(0.1, 0.2) >> 0.3
 * floatObj.multiply(19.9, 100) >> 1990
 *
 */
var floatObj = function() {
 
 /*
  * 判断obj是否为一个整数
  */
 function isInteger(obj) {
  return Math.floor(obj) === obj
 }
 
 /*
  * 将一个浮点数转成整数，返回整数和倍数。如 3.14 >> 314，倍数是 100
  * @param floatNum {number} 小数
  * @return {object}
  * {times:100, num: 314}
  */
 function toInteger(floatNum) {
  var ret = {times: 0, num: 0}
  if (isInteger(floatNum)) {
   ret.num = floatNum
   return ret
  }
  var strfi = floatNum + ''
  var dotPos = strfi.indexOf('.')
  var len = strfi.substr(dotPos+1).length
  var times = Math.pow(10, len)
  var intNum = parseInt(floatNum * times + 0.5, 10)
  ret.times = times
  ret.num = intNum
  return ret
 }
 
 /*
  * 核心方法，实现加减乘除运算，确保不丢失精度
  * 思路：把小数放大为整数（乘），进行算术运算，再缩小为小数（除）
  *
  * @param a {number} 运算数1
  * @param b {number} 运算数2
  * @param digits {number} 精度，保留的小数点数，比如 2, 即保留为两位小数
  * @param op {string} 运算类型，有加减乘除（add/subtract/multiply/divide）
  *
  */
 function operation(a, b, digits, op) {
  var o1 = toInteger(a)
  var o2 = toInteger(b)
  var max = o1.times > o2.times ? o1.times : o2.times
  var result = null
  switch (op) {
   case 'add':
    result = o1.num + o2.num
    break
   case 'subtract':
    result = o1.num - o2.num
    break
   case 'multiply':
    result = o1.num * o2.num
    break
   case 'divide':
    result = o1.num / o2.num
    break
  }
  return result / max
 }
 
 // 加减乘除的四个接口
 function add(a, b, digits) {
  return operation(a, b, digits, 'add')
 }
 function subtract(a, b, digits) {
  return operation(a, b, digits, 'subtract')
 }
 function multiply(a, b, digits) {
  return operation(a, b, digits, 'multiply')
 }
 function divide(a, b, digits) {
  return operation(a, b, digits, 'divide')
 }
 
 // exports
 return {
  add: add,
  subtract: subtract,
  multiply: multiply,
  divide: divide
 }
 
}();

ToFixed est corrigé comme suit

// toFixed 修复
function toFixed(num, s) {
 var times = Math.pow(10, s)
 var des = num * times + 0.5
 des = parseInt(des, 10) / times
 return des + ''
}

Ce qui précède concerne le problème de la perte de précision numérique JavaScript. Il analyse les problèmes typiques, analyse les raisons de la perte de précision numérique et partage également des solutions. J'espère que cela sera utile à l'apprentissage de chacun.