Explication détaillée du code de l'arborescence des préfixes javascript trie

Cet article présente principalement des exemples d'arbres de recherche de mots JavaScript. Il présente le concept et la mise en œuvre de trie en détail. Il a une certaine valeur de référence. J'espère qu'il pourra aider tout le monde.

Introduction

L'arbre de Trie (du mot récupération), également connu sous le nom de mot préfixe, arbre de recherche de mots, arbre de dictionnaire, est une structure arborescente, une variante haha ​​A. de l'arbre grec, une structure multi-arbre utilisée pour une récupération rapide.

Ses avantages sont les suivants : minimiser les comparaisons de chaînes inutiles et l'efficacité des requêtes est supérieure à celle des tables de hachage.

L'idée centrale de Trie est d'échanger de l'espace contre du temps. Utilisez le préfixe commun des chaînes pour réduire le temps de requête et améliorer l'efficacité.

L'arbre de Trie a aussi ses défauts. En supposant que nous traitons uniquement des lettres et des chiffres, alors chaque nœud a au moins 52+10 nœuds enfants. Pour économiser de la mémoire, nous pouvons utiliser des listes chaînées ou des tableaux. En JS, nous utilisons directement les tableaux, car les tableaux JS sont dynamiques et sont dotés d'une optimisation intégrée.

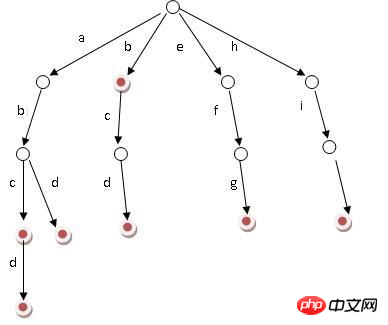
Propriétés de base

1. Le nœud racine ne contient pas de caractères, et chaque nœud enfant à l'exception du nœud racine contient un caractère

2. Du nœud racine à un certain nœud. Les caractères passant sur le chemin sont connectés, ce qui est la chaîne correspondant au nœud

3. Tous les sous-nœuds de chaque nœud contiennent des caractères différents

Mise en œuvre du programme

// by 司徒正美
class Trie {
 constructor() {
  this.root = new TrieNode();
 }
 isValid(str) {
  return /^[a-z1-9]+$/i.test(str);
 }
 insert(word) {
  // addWord
  if (this.isValid(word)) {
   var cur = this.root;
   for (var i = 0; i < word.length; i++) {
    var c = word.charCodeAt(i);
    c -= 48; //减少”0“的charCode
    var node = cur.son[c];
    if (node == null) {
     var node = (cur.son[c] = new TrieNode());
     node.value = word.charAt(i);
     node.numPass = 1; //有N个字符串经过它
    } else {
     node.numPass++;
    }
    cur = node;
   }
   cur.isEnd = true; //樯记有字符串到此节点已经结束
   cur.numEnd++; //这个字符串重复次数

   return true;
  } else {
   return false;
  }
 }
 remove(word){
   if (this.isValid(word)) {
     var cur = this.root;
     var array = [], n = word.length
     for (var i = 0; i < n; i++) {
       var c = word.charCodeAt(i);
       c = this.getIndex(c)
       var node = cur.son[c];
       if(node){
         array.push(node)
         cur = node
       }else{
         return false
       }
 
     }
     if(array.length === n){
       array.forEach(function(){
         el.numPass--
       })
       cur.numEnd --
       if( cur.numEnd == 0){
         cur.isEnd = false
       } 
     }
   }else{
     return false
   }
 }
 preTraversal(cb){//先序遍历
    function preTraversalImpl(root, str, cb){ 
      cb(root, str);
      for(let i = 0,n = root.son.length; i < n; i ++){
        let node = root.son[i];
        if(node){
          preTraversalImpl(node, str + node.value, cb);
        }
      }
    } 
    preTraversalImpl(this.root, "", cb);
  }
 // 在字典树中查找是否存在某字符串为前缀开头的字符串(包括前缀字符串本身)
 isContainPrefix(word) {
  if (this.isValid(word)) {
   var cur = this.root;
   for (var i = 0; i < word.length; i++) {
    var c = word.charCodeAt(i);
    c -= 48; //减少”0“的charCode
    if (cur.son[c]) {
     cur = cur.son[c];
    } else {
     return false;
    }
   }
   return true;
  } else {
   return false;
  }
 }
 isContainWord(str) {
  // 在字典树中查找是否存在某字符串(不为前缀)
  if (this.isValid(word)) {
   var cur = this.root;
   for (var i = 0; i < word.length; i++) {
    var c = word.charCodeAt(i);
    c -= 48; //减少”0“的charCode
    if (cur.son[c]) {
     cur = cur.son[c];
    } else {
     return false;
    }
   }
   return cur.isEnd;
  } else {
   return false;
  }
 }
 countPrefix(word) {
  // 统计以指定字符串为前缀的字符串数量
  if (this.isValid(word)) {
   var cur = this.root;
   for (var i = 0; i < word.length; i++) {
    var c = word.charCodeAt(i);
    c -= 48; //减少”0“的charCode
    if (cur.son[c]) {
     cur = cur.son[c];
    } else {
     return 0;
    }
   }
   return cur.numPass;
  } else {
   return 0;
  }
 }
 countWord(word) {
  // 统计某字符串出现的次数方法
  if (this.isValid(word)) {
   var cur = this.root;
   for (var i = 0; i < word.length; i++) {
    var c = word.charCodeAt(i);
    c -= 48; //减少”0“的charCode
    if (cur.son[c]) {
     cur = cur.son[c];
    } else {
     return 0;
    }
   }
   return cur.numEnd;
  } else {
   return 0;
  }
 }
}

class TrieNode {
 constructor() {
  this.numPass = 0;//有多少个单词经过这节点
  this.numEnd = 0; //有多少个单词就此结束
  this.son = [];
  this.value = ""; //value为单个字符
  this.isEnd = false;
 }
}

Concentrons-nous sur la méthode d'insertion de TrieNode et Trie. Étant donné que l'arborescence du dictionnaire est principalement utilisée pour les statistiques de fréquence des mots, elle possède de nombreux attributs de nœud, notamment numPass, numEnd, mais des attributs très importants.

La méthode d'insertion est utilisée pour insérer des mots lourds. Avant de commencer, nous devons déterminer si le mot est légal. Les caractères spéciaux et les espaces ne peuvent pas apparaître. Lors de l'insertion, les caractères sont divisés et placés dans chaque nœud. numPass doit être modifié à chaque fois qu'un nœud est passé.

Optimisation

Maintenant dans chacune de nos méthodes, il y a une opération de c=-48. En fait, il y a d'autres caractères entre les chiffres, les lettres majuscules et les lettres minuscules, donc. Cela entraînera une perte d'espace inutile

// by 司徒正美
getIndex(c){
   if(c < 58){//48-57
     return c - 48
   }else if(c < 91){//65-90
     return c - 65 + 11
   }else {//> 97 
     return c - 97 + 26+ 11
   }
 }

Ensuite, la méthode pertinente consiste à changer c-= 48 en c = this.getIndex(c)

Test

var trie = new Trie(); 
  trie.insert("I"); 
  trie.insert("Love"); 
  trie.insert("China"); 
  trie.insert("China"); 
  trie.insert("China"); 
  trie.insert("China"); 
  trie.insert("China"); 
  trie.insert("xiaoliang"); 
  trie.insert("xiaoliang"); 
  trie.insert("man"); 
  trie.insert("handsome"); 
  trie.insert("love"); 
  trie.insert("Chinaha"); 
  trie.insert("her"); 
  trie.insert("know"); 
  var map = {}
  trie.preTraversal(function(node, str){
    if(node.isEnd){
     map[str] = node.numEnd
    }
  })
  for(var i in map){
    console.log(i+" 出现了"+ map[i]+" 次")
  }
  console.log("包含Chin（包括本身）前缀的单词及出现次数："); 
  //console.log("China")
  var map = {}
  trie.preTraversal(function(node, str){
    if(str.indexOf("Chin") === 0 && node.isEnd){
      map[str] = node.numEnd
    }
   })
  for(var i in map){
    console.log(i+" 出现了"+ map[i]+" 次")
  }

Comparaison de l'arbre de Trie et d'autres structures de données

Arbre de Trie et arbre de recherche binaire

L'arbre de recherche binaire doit être la première structure arborescente avec laquelle nous entrons en contact. Nous savons que lorsque la taille des données est n, l'arbre de recherche binaire. inserts, La complexité temporelle des opérations de recherche et de suppression n'est généralement que O(log n). Dans le pire des cas, tous les nœuds de l'arborescence entière n'ont qu'un seul nœud enfant, qui dégénère en un tableau linéaire à ce moment-là. des opérations d’insertion, de recherche et de suppression est complexe. Le degré est O(n).

Normalement, la hauteur n de l'arbre Trie est bien supérieure à la longueur m de la chaîne de recherche, donc la complexité temporelle de l'opération de recherche est généralement O(m), et la complexité temporelle dans le pire des cas est O (n). Il est facile de voir que la recherche dans le pire des cas dans un arbre de Trie est plus rapide que dans un arbre de recherche binaire.

L'arbre de Trie dans cet article utilise des chaînes comme exemples. En fait, il a des exigences strictes sur l'adéquation de la clé. Si la clé est un nombre à virgule flottante, l'arbre de Trie entier peut être extrêmement. long et les nœuds peuvent être La lisibilité est également très mauvaise. Dans ce cas, il n'est pas approprié d'utiliser l'arbre de Trie pour sauvegarder les données. Ce problème n'existe pas avec l'arbre de recherche binaire.

Arbre de Trie et table de hachage

Considérez le problème du conflit de hachage. Nous disons généralement que la complexité d'une table de hachage est O(1). En fait, à proprement parler, c'est la complexité d'une table de hachage qui est proche de la perfection. De plus, nous devons également tenir compte des besoins de la fonction de hachage elle-même. pour parcourir la chaîne de recherche, et la complexité est O(m ). Lorsque différentes clés sont mappées à la « même position » (en considérant le hachage fermé, cette « même position » peut être remplacée par une liste chaînée ordinaire), la complexité de la recherche dépend du nombre de nœuds sous le numéro « même position », par conséquent, dans le pire des cas, la table de hachage peut également devenir une liste chaînée unidirectionnelle.

Les arbres Trie peuvent être triés plus facilement selon l'ordre alphabétique des clés (l'arbre entier est parcouru une fois dans l'ordre), ce qui est différent de la plupart des tables de hachage (les tables de hachage ont généralement des clés différentes pour différentes clés). est désordonné).

Dans des circonstances idéales, la table de hachage peut rapidement atteindre la cible à une vitesse O(1). Si cette table est très volumineuse et doit être placée sur le disque, l'accès à la recherche de la table de hachage sera plus rapide. dans des circonstances idéales, cela ne doit être fait qu'une seule fois ; mais le nombre d'accès au disque par l'arborescence Trie doit être égal à la profondeur du nœud.

Souvent, un arbre Trie nécessite plus d'espace qu'une table de hachage. Si l'on considère la situation où un nœud stocke un caractère, il n'y a aucun moyen de l'enregistrer en tant que bloc séparé lors de l'enregistrement d'une chaîne. La compression des nœuds de l'arbre de Trie peut atténuer considérablement ce problème, qui sera abordé plus tard.

Amélioration de l'arbre de Trie

Bitwise Trie (Bitwise Trie)

En principe, il est similaire à l'arbre de Trie ordinaire, sauf que l'arbre de Trie ordinaire Magasins d'arborescence Trie La plus petite unité est un caractère, mais Bitwise Trie ne stocke que des bits. L'accès aux données binaires est directement implémenté une seule fois par l'instruction CPU. Pour les données binaires, il est théoriquement plus rapide que l'arbre de Trie ordinaire.

Compression des nœuds.

Compression de branches : pour un arbre Trie stable, des opérations de recherche et de lecture sont essentiellement effectuées, et certaines branches peuvent être compressées. Par exemple, l'auberge de la branche la plus à droite de la figure précédente peut être directement compressée en un nœud « inn » sans exister en tant que sous-arbre régulier. L'arbre Radix est basé sur ce principe pour résoudre le problème de l'arbre de Trie trop profond.

Tableau de mappage de nœuds : Cette méthode est également utilisée lorsque les nœuds de l'arbre Trie peuvent avoir été presque entièrement déterminés pour chaque état du nœud dans l'arbre Trie, si le nombre total d'états est répété plusieurs fois. , via un élément Représenté comme un tableau multidimensionnel de nombres (tel que Triple Array Trie), la surcharge d'espace liée au stockage de l'arbre Trie lui-même sera plus petite, bien qu'une table de mappage supplémentaire soit introduite.

Application de l'arbre de préfixes

L'arbre de préfixes est toujours facile à comprendre, et son application est également très large.

(1) Récupération rapide des chaînes

La complexité temporelle de la requête de l'arborescence du dictionnaire est O(logL), où L est la longueur de la chaîne. L'efficacité est donc encore relativement élevée. Les arbres de dictionnaire sont plus efficaces que les tables de hachage.

(2) Tri des chaînes

À partir de la figure ci-dessus, nous pouvons facilement voir que les mots sont triés et que l'ordre alphabétique est parcouru en premier. Réduisez les sous-chaînes communes inutiles.

(3) Le préfixe commun le plus long

Le préfixe commun le plus long de inn et int est in. Lorsque vous parcourez l'arborescence du dictionnaire jusqu'à la lettre n, le préfixe commun de ces mots est in.

(4) Faire correspondre automatiquement les préfixes et afficher les suffixes

Lorsque nous utilisons un dictionnaire ou un moteur de recherche, saisissez appl, et un tas de choses avec le préfixe appl seront automatiquement affichées. Ensuite, cela peut être réalisé via une arborescence de dictionnaire. Comme mentionné précédemment, l'arborescence de dictionnaire peut trouver le préfixe commun. Il suffit de parcourir et d'afficher les suffixes restants.

Recommandations associées :

À propos de uery EasyUI combiné avec le didacticiel de développement de la page d'arrière-plan de ztrIee

À propos de l'arbre de dictionnaire Trie en php Exemple de la méthode de définition d'implémentation

Word PHP implémente l'arbre Trie (arbre de dictionnaire)

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!