Maison >interface Web >tutoriel HTML >Canvas implémente la courbe de Bézier d'ordre élevé
Canvas implémente la courbe de Bézier d'ordre élevé
- 小云云original
- 2018-01-13 09:40:132886parcourir
Cet article présente principalement l'implémentation de la courbe de Bézier d'ordre élevé (générateur de courbe de Bézier d'ordre N) dans Canvas. L'éditeur pense que c'est assez bon. Maintenant, je vais le partager avec vous et le donner comme référence. Suivons l'éditeur et jetons un œil. J'espère que cela pourra aider tout le monde.
Écrivez d'abord
Étant donné que le canevas natif ne prend en charge que les courbes de Bézier du troisième ordre, que dois-je faire si je souhaite ajouter plusieurs points de contrôle ? (Même les courbes les plus complexes peuvent être simulées avec Bézier de troisième ordre.) Dans le même temps, il nous est difficile de comprendre clairement la position des points de contrôle de Bézier de manière très intuitive. Dans quelle mesure pouvons-nous définir les points de contrôle pour former la courbe. on veut ? Afin de résoudre les deux problèmes ci-dessus, il ne semble pas y avoir de solution de niveau N (version js) dans la communauté, donc cette fois l'auteur est très sérieux au sujet de l'open source bezierMaker.js !
bezierMaker.js prend théoriquement en charge la génération de courbes de Bézier d'ordre N et fournit également un terrain de test permettant aux développeurs d'ajouter et de faire glisser des points de contrôle pour finalement générer un ensemble d'animations de dessin. Il est très intuitif pour les développeurs de connaître les différentes courbes de génération correspondant aux points de contrôle à différentes positions.
Si vous aimez ce travail, bienvenue chez Star, après tout, les étoiles se méritent durement. .
Adresse du projet : ici✨✨✨
Pourquoi un site de test est-il nécessaire ?
Lorsque vous dessinez des courbes de Bézier d'ordre élevé complexes, vous ne pouvez pas connaître l'emplacement précis des points de contrôle de la courbe dont vous avez besoin. En simulant dans le champ de test, les valeurs des coordonnées des points de contrôle peuvent être obtenues en temps réel. Les coordonnées des points obtenues peuvent être converties en un tableau d'objets et transmises à la classe BezierMaker pour générer la courbe cible
Rendu 

Fonction
- [x ] N'importe quel nombre de points de contrôle peut être ajouté au site de test
- [x] Le site de test prend en charge l'affichage de l'animation de formation du dessin de courbe
- [x] Les points de contrôle peuvent être déplacés librement
- [x] Prend en charge l'affichage des lignes tangentes dans le processus de formation des courbes de Bézier
- [x] Le dessin des courbes de Bézier d'ordre 3 et inférieur utilise l'API native
Présentation de
<script src="./bezierMaker.js"></script>
Dessinez
l'effet ci-dessus L'image montre l'utilisation du site de test Après avoir obtenu les coordonnées précises des points de contrôle via le site de test, vous pouvez appeler bezierMaker.js. pour tracer directement la courbe./**
* canvas canvas的dom对象
* bezierCtrlNodesArr 控制点数组,包含x,y坐标
* color 曲线颜色
*/
var canvas = document.getElementById('canvas')
//3阶之前采用原生方法实现
var arr0 = [{x:70,y:25},{x:24,y:51}]
var arr1 = [{x:233,y:225},{x:170,y:279},{x:240,y:51}]
var arr2 = [{x:23,y:225},{x:70,y:79},{x:40,y:51},{x:300, y:44}]
var arr3 = [{x:333,y:15},{x:70,y:79},{x:40,y:551},{x:170,y:279},{x:17,y:239}]
var arr4 = [{x:53,y:85},{x:170,y:279},{x:240,y:551},{x:70,y:79},{x:40,y:551},{x:170,y:279}]
var bezier0 = new BezierMaker(canvas, arr0, 'black')
var bezier1 = new BezierMaker(canvas, arr1, 'red')
var bezier2 = new BezierMaker(canvas, arr2, 'blue')
var bezier3 = new BezierMaker(canvas, arr3, 'yellow')
var bezier4 = new BezierMaker(canvas, arr4, 'green')
bezier0.drawBezier()
bezier1.drawBezier()
bezier2.drawBezier()
bezier3.drawBezier()
bezier4.drawBezier()Résultat du dessin

Principes de base
Dessiner des courbes de BézierLe point essentiel du dessin des courbes de Bézier réside dans l'application de la formule de Bézier :
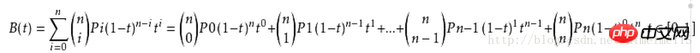
BezierMaker.prototype.bezier = function(t) { //贝塞尔公式调用
var x = 0,
y = 0,
bezierCtrlNodesArr = this.bezierCtrlNodesArr,
//控制点数组
n = bezierCtrlNodesArr.length - 1,
self = this
bezierCtrlNodesArr.forEach(function(item, index) {
if(!index) {
x += item.x * Math.pow(( 1 - t ), n - index) * Math.pow(t, index)
y += item.y * Math.pow(( 1 - t ), n - index) * Math.pow(t, index)
} else {
//factorial为阶乘函数
x += self.factorial(n) / self.factorial(index) / self.factorial(n - index) * item.x * Math.pow(( 1 - t ), n - index) * Math.pow(t, index)
y += self.factorial(n) / self.factorial(index) / self.factorial(n - index) * item.y * Math.pow(( 1 - t ), n - index) * Math.pow(t, index)
}
})
return {
x: x,
y: y
}
}Parcourez tous les points et calculez la position actuelle sur la courbe de Bézier en fonction de la valeur de la proportion actuelle t (0<=t<=1) Le point coordonnées x, y. L'auteur divise la valeur de t en 1000 parties, soit t+=0,01 pour chaque opération. Les x et y calculés à ce moment sont les points après que la courbe de Bézier soit divisée en 1000 parties. Lorsque la valeur t passe de 0 à 1 1 000 fois, 1 000 coordonnées x, y correspondantes sont générées et une courbe de Bézier d'ordre élevé peut être simulée en traçant des points et des lignes en séquence. L'auteur expliquera spécifiquement le calcul de la formule de Bézier dans un article ultérieur. Il vous suffit maintenant de savoir que nous utilisons la formule de Bézier pour calculer les points auxquels la courbe de Bézier réelle est divisée en 1000 parties égales. , une courbe de classe peut être simulée en reliant chaque point par une ligne droite. Pour la mise en œuvre de l'animation de génération de courbe de Bézier sur le terrain de simulation Cette partie du code pertinent peut être consultée iciL'idée générale est d'utiliser la récursivité pour contrôler chaque couche Les points sont traités comme des fonctions de Bessel de premier ordre pour calculer la couche suivante de points de contrôle et les connexions correspondantes. L'auteur laissera la logique spécifique jusqu'à l'explication approfondie des principes de la formule de la courbe de Bézier pour démêler les principes de génération d'animation du site de test~Recommandations associées :
Utilisez CSS pour créer une courbe de Bézier
Explication détaillée de l'application de la courbe de Bézier
Démonstration de code pour l'implémentation de l'effet de courbe de Bézier sur toile
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

