Explication détaillée de la base théorique du réseau neuronal et de la méthode de mise en œuvre de Python

Le réseau de neurones artificiels est un modèle mathématique algorithmique qui imite les caractéristiques comportementales des réseaux de neurones animaux et effectue un traitement d'informations parallèle distribué. Ce type de réseau s'appuie sur la complexité du système pour atteindre l'objectif de traitement de l'information en ajustant les relations interconnectées entre un grand nombre de nœuds internes, et a la capacité de s'auto-apprendre et de s'adapter. Cet article présente principalement les bases théoriques du réseau neuronal et l'explication détaillée de la mise en œuvre de Python. Il a une certaine valeur de référence. Les amis dans le besoin peuvent s'y référer.

1. Réseau neuronal avant multicouche

Le réseau neuronal avant multicouche se compose de trois parties : couche de sortie, couche cachée, sortie. Couche, chaque couche est composée d'unités ;

La couche d'entrée est transmise à partir du vecteur de caractéristiques d'instance de l'ensemble d'entraînement et transmise à la couche suivante via le poids du nœud de connexion. la couche est l'entrée de la couche suivante ;Le nombre de couches cachées est arbitraire, il n'y a qu'une seule couche d'entrée et il n'y a qu'une seule couche de sortie

À l'exclusion de la couche d'entrée, la somme du nombre de couches cachées ; les couches et les couches de sortie sont n, alors le réseau neuronal C'est ce qu'on appelle un réseau neuronal à n couches. La figure suivante montre un réseau neuronal à 2 couches

Somme pondérée en une couche, transformée et sortie selon une méthode non linéaire ; équations ; Théoriquement, s'il y a suffisamment de couches cachées et suffisamment grandes L'ensemble de formation peut simuler n'importe quelle équation

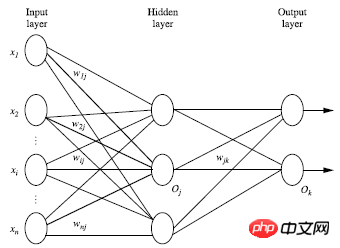
2. Concevoir la structure du réseau neuronal ;

utilisation Avant d'utiliser un réseau de neurones, il est nécessaire de déterminer le nombre de couches du réseau de neurones et le nombre d'unités dans chaque couche

Afin de Pour accélérer le processus d'apprentissage, le vecteur de caractéristiques doit généralement être standardisé entre 0 et 1 avant d'être transmis à la couche d'entrée ;

Les variables discrètes peuvent être codées en valeurs qui peuvent être attribuées à chaque entrée. unité correspondant à une valeur propre

Par exemple : la valeur propre A peut avoir trois valeurs (a0, a1, a2), Alors 3 unités d'entrée peuvent être utilisées pour représenter A

Si A=a0 , la valeur unitaire représentant a0 est 1, et le reste est 0 ;
Si A=a1, la valeur unitaire représentant a1 est 1 , le reste est 0
Si A=a2, la valeur unitaire représentant a2 est 1, et le reste est 0 ;

Le réseau neuronal résout non seulement le problème de classification, mais peut également résoudre les problèmes de régression. Pour les problèmes de classification, s'il y a deux catégories, une unité de sortie (0 et 1) peut être utilisée pour représenter les deux catégories respectivement. S'il y a plus de deux catégories, chaque catégorie est représentée par une unité de sortie, donc le nombre d'unités ; dans la couche de sortie est généralement égale à une quantité.

Il n'existe pas de règles claires pour concevoir le nombre optimal de couches cachées. Les expériences sont généralement améliorées en fonction des erreurs et de la précision des tests expérimentaux.

3. Méthode de validation croisée

Comment calculer la précision ? La méthode la plus simple consiste à utiliser un ensemble d'ensembles de formation et d'ensembles de test. L'ensemble de formation est formé pour obtenir le modèle. L'ensemble de test est entré dans le modèle pour obtenir les résultats des tests. Les résultats des tests sont comparés aux étiquettes réelles du modèle. Ensemble de test pour obtenir la précision.

Une méthode couramment utilisée dans le domaine du machine learning est la méthode de validation croisée. Un ensemble de données n'est pas divisé en 2 parties, mais peut être divisé en 10 parties

La 1ère fois : la 1ère partie est utilisée comme ensemble de test, et les 9 parties restantes sont utilisées comme ensemble d'entraînement. ;
La 2ème fois : la 2ème partie est utilisée comme ensemble de test, et les 9 ensembles restants sont utilisés comme ensembles d'entraînement
...

Après 10 fois d'entraînement, 10 ensembles ; de précision sont obtenus, et la précision moyenne de ces 10 ensembles de données est obtenue. Ici 10 est un cas particulier. D'une manière générale, les données sont divisées en k parties et l'algorithme est appelé K-foldcrossvalidation. Autrement dit, chaque fois qu'une des k parties est sélectionnée comme ensemble de test, les k-1 parties restantes sont utilisées comme ensemble de test. ensemble d'entraînement. Répétez k fois, et finalement la précision moyenne est obtenue, est une méthode plus scientifique et plus précise.

4. Algorithme BP

Traitement des instances dans l'ensemble d'entraînement par itération ; 🎜>Comparez la différence entre la valeur prédite et la valeur réelle après avoir traversé le réseau neuronal ;

Direction inverse (depuis la couche de sortie => couche cachée => couche d'entrée) pour minimiser l'erreur de mise à jour de chaque connexion. poids de

Initialiser les poids et les biais : Initialisez aléatoirement entre -1 et 1 (ou autre), chaque unité a un biais pour chaque instance d'entraînement X, effectuez les étapes suivantes :

À partir de l'entrée ; Transmission avant couche :

Analyse combinée au diagramme schématique du réseau neuronal :

De la couche d'entrée à la couche cachée :

De la couche cachée à la couche de sortie :

En résumant les deux formules, nous pouvons obtenir :

Ij est la valeur unitaire de la couche actuelle, et Oi est la unité de la valeur de la couche précédente, wij est la valeur de poids reliant les deux valeurs unitaires entre les deux couches, et sitaj est la valeur de biais de chaque couche. Nous devons effectuer une transformation non linéaire sur la sortie de chaque couche. Le diagramme schématique est le suivant :

La sortie de la couche actuelle est Ij, et f est la transformation non linéaire. fonction, également connue sous le nom de fonction d'activation, définie comme suit :

C'est-à-dire que la sortie de chaque couche est :

De cette façon, la valeur d'entrée peut être transmise. Obtenez la valeur de sortie de chaque couche.

2. Propagation inverse selon l'erreur Pour la couche de sortie : où Tk est la vraie valeur et Ok est la valeur prédite

Pour la cachée. couche :

Mise à jour du poids : où l est le taux d'apprentissage

Mise à jour du biais :

3. Conditions de résiliation

La mise à jour biaisée est inférieure à un certain seuil
Le taux d'erreur prévu est inférieur à un certain seuil
Le nombre prédéfini de ; cycles est atteint ;

4. Fonction de transformation non linéaire

La fonction de transformation non linéaire f mentionnée ci-dessus peut généralement utiliser deux fonctions :

(1) fonction tanh(x) :

tanh(x)=sinh(x)/cosh(x)
sinh(x)=(exp(x)-exp(-x))/2
cosh(x)=( exp( x)+exp(-x))/2

(2) Fonction logique, la fonction logique utilisée dans cet article est

5. Implémentation Python de Réseau neuronal BP

Vous devez d'abord importer le module numpy

import numpy as np

Définir la fonction de transformation non linéaire, car vous devez également utiliser La forme dérivée de la fonction, alors définissez ensemble

def tanh(x):
  return np.tanh(x)
def tanh_deriv(x):
  return 1.0 - np.tanh(x)*np.tanh(x)
def logistic(x):
  return 1/(1 + np.exp(-x))
def logistic_derivative(x):
  return logistic(x)*(1-logistic(x))

pour concevoir la forme du réseau neuronal BP (combien de couches , combien d'unités par couche), en utilisant l'objet orienté, principalement quelle fonction non linéaire choisir et initialiser les poids. Les calques sont une liste contenant le nombre d'unités dans chaque calque.

class NeuralNetwork:
  def __init__(self, layers, activation='tanh'):
    """
    :param layers: A list containing the number of units in each layer.
    Should be at least two values
    :param activation: The activation function to be used. Can be
    "logistic" or "tanh"
    """
    if activation == 'logistic':
      self.activation = logistic
      self.activation_deriv = logistic_derivative
    elif activation == 'tanh':
      self.activation = tanh
      self.activation_deriv = tanh_deriv
 
    self.weights = []
    for i in range(1, len(layers) - 1):
      self.weights.append((2*np.random.random((layers[i - 1] + 1, layers[i] + 1))-1)*0.25)
      self.weights.append((2*np.random.random((layers[i] + 1, layers[i + 1]))-1)*0.25)

Implémenter l'algorithme

  def fit(self, X, y, learning_rate=0.2, epochs=10000):
    X = np.atleast_2d(X)
    temp = np.ones([X.shape[0], X.shape[1]+1])
    temp[:, 0:-1] = X
    X = temp
    y = np.array(y)
 
    for k in range(epochs):
      i = np.random.randint(X.shape[0])
      a = [X[i]]
 
      for l in range(len(self.weights)):
        a.append(self.activation(np.dot(a[l], self.weights[l])))
      error = y[i] - a[-1]
      deltas = [error * self.activation_deriv(a[-1])]
 
      for l in range(len(a) - 2, 0, -1):
        deltas.append(deltas[-1].dot(self.weights[l].T)*self.activation_deriv(a[l]))
      deltas.reverse()
 
      for i in range(len(self.weights)):
        layer = np.atleast_2d(a[i])
        delta = np.atleast_2d(deltas[i])
        self.weights[i] += learning_rate * layer.T.dot(delta)

Implémenter la prédiction

  def predict(self, x):
    x = np.array(x)
    temp = np.ones(x.shape[0]+1)
    temp[0:-1] = x
    a = temp
    for l in range(0, len(self.weights)):
      a = self.activation(np.dot(a, self.weights[l]))
    return a

Nous donnons un ensemble de nombres pour la prédiction. Le fichier de programme que nous avons enregistré ci-dessus est nommé BP

from BP import NeuralNetwork
import numpy as np
 
nn = NeuralNetwork([2,2,1], 'tanh')
x = np.array([[0,0], [0,1], [1,0], [1,1]])
y = np.array([1,0,0,1])
nn.fit(x,y,0.1,10000)
for i in [[0,0], [0,1], [1,0], [1,1]]:
  print(i, nn.predict(i))

Les résultats sont les suivants :

([0, 0], array([ 0.99738862]))
([0, 1], array([ 0.00091329]))
([1, 0], array([ 0.00086846]))
([1, 1], array([ 0.99751259]))

Recommandations associées :

À propos de numpy pour définir de manière flexible réseaux de neurones en Python Exemples de structures

Partage d'exemples simples d'implémentation de réseaux de neurones récursifs en Python

Explication graphique et textuelle détaillée de réseaux neuronaux simples algorithme de réseau implémenté en JavaScript

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!