Maison >interface Web >js tutoriel >Analyse d'exemples de programmation dynamique d'algorithmes avancés JavaScript
Analyse d'exemples de programmation dynamique d'algorithmes avancés JavaScript
- 小云云original
- 2017-12-07 16:01:112095parcourir
En fait, dans notre développement front-end, peu d'algorithmes avancés sont utilisés. Dans la plupart des cas, les instructions if, for, switch, etc. peuvent être résolues. Si c'est un peu plus compliqué, vous pourriez penser à utiliser la récursivité pour le résoudre. Cet article présente principalement la programmation dynamique des algorithmes de programmation JavaScript avancés et analyse les principes, les techniques de mise en œuvre et les précautions d'utilisation associées de l'algorithme de programmation dynamique JavaScript sous forme d'exemples. Les amis dans le besoin peuvent s'y référer.
Mais il convient de noter que la récursivité est simple à écrire, mais son efficacité d'exécution réelle n'est pas élevée.
Regardons à nouveau l'algorithme de programmation dynamique :
La solution de programmation dynamique commence par le bas pour résoudre le problème, résout tous les petits problèmes, puis les fusionne en une solution globale pour résoudre le tout le problème. Gros problème.
Exemple (Calcul de la séquence de Fibonacci)
La séquence de Fibonacci fait référence à une séquence de 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 , 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368...
Cette séquence part du 3ème élément Initialement, chaque terme est égal à la somme du précédent deux termes.
Pour cette séquence, vous pouvez utiliser une fonction récursive pour calculer la nième valeur
// 斐波那契数列
function recurFib(n) {
if(n < 2){
return n ;
}else {
// document.write("第"+(n-1)+"次计算 n-1="+(n-1)+recurFib(n-1)+' ');
// document.write("n-2="+(n-2)+recurFib(n-2)+"<br>");
return recurFib(n-1)+recurFib(n-2)
}
}En effet est un code très concis. Le code commenté ci-dessus est utilisé pour afficher combien de fois la fonction doit être exécutée lorsque n =. Cependant, une personne avisée peut voir en un coup d'œil que lorsque n augmente, le nombre d'exécutions le sera également. être très élevée. La terreur grandit.
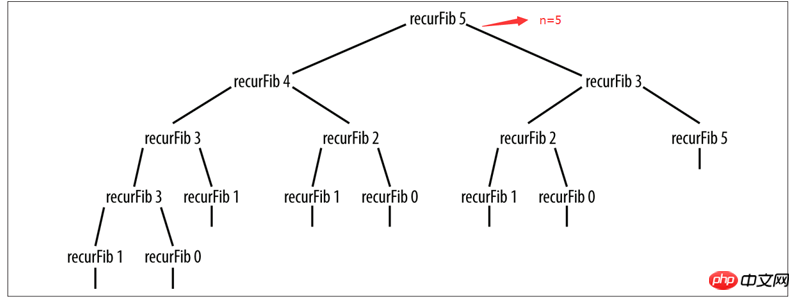
Quand n=5, l'arbre de récursivité est devenu très grand... On peut prédire que lorsque n=10, voire n=100...
Comprenant la différence d'efficacité d'exécution des fonctions récursives, regardons comment la programmation dynamique est effectuée
function dynFib(n) {
let val = [];
for(let i = 0; i <= n; ++i){
val[i]=0;
}
if(n ===1 || n === 2){
return 1;
}
else {
val[1] =1;
val[2] = 2;
for(let i = 3; i <= n; ++i){
val[i] = val [i-1] +val[i-2] ;
}
}
return val[n-1]
}Réussi Le résultat intermédiaire est stocké dans le tableau val. Si le nombre de Fibonacci à calculer est 1 ou 2, alors l'instruction if renverra 1. Sinon, les valeurs 1 et 2 seront stockées aux positions 1 et 2 du tableau val.
La boucle passera de 3 aux paramètres d'entrée, attribuant à chaque élément du tableau la somme des deux premiers éléments, la boucle se termine et la valeur du dernier élément du tableau est la valeur calculée finale de Fibonacci valeur, cette valeur sera également utilisée comme valeur de retour de la fonction.
Ensuite, vous pouvez écrire une fonction de test simple pour comparer le temps d'exécution des deux.
// 定义一个测试函数,将待测函数作为参数传入
function test(func,n){
let start = new Date().getTime();//起始时间
let res = func(n);//执行待测函数
document.write('<br>'+'当n='+n+'的时候 '+res+'<br>');
let end = new Date().getTime();//结束时间
return (end - start)+"ms";//返回函数执行需要时间
}Exécution de la fonction d'impression
let time = test(recurFib,40); document.write(time); let time2 = test(dynFib,40); document.write(time2);
Les résultats sont les suivants :

Enfin, vous avez peut-être réalisé que lors du calcul de la séquence de Fibonacci à l'aide d'un schéma itératif, vous pouvez le faire sans en utilisant un tableau de.
La raison pour laquelle les tableaux sont nécessaires est que les algorithmes de programmation dynamique doivent généralement enregistrer les résultats intermédiaires.
Ce qui suit est la version itérative de la définition de la fonction Fibonacci
function iterFib(n) {
let last = 1;
let nextLast = 1;
let result = 1;
for (let i = 2; i < n; ++i) {
result = last + nextLast;
nextLast = last;
last = result;
}
return result;
}Bien sûr, cette version itérative est la même chose que La version array est tout aussi efficace.

Recommandations associées :
Programmation dynamique de l'apprentissage des algorithmes PHP
Programmation dynamique de l'apprentissage des algorithmes PHP (2)
Explication détaillée du problème de changement de la programmation dynamique
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Une analyse approfondie du composant de groupe de liste Bootstrap
- Explication détaillée du currying de la fonction JavaScript
- Exemple complet de génération de mot de passe JS et de détection de force (avec téléchargement du code source de démonstration)
- Angularjs intègre l'interface utilisateur WeChat (weui)
- Comment basculer rapidement entre le chinois traditionnel et le chinois simplifié avec JavaScript et l'astuce permettant aux sites Web de prendre en charge le basculement entre les compétences en chinois simplifié et traditionnel_javascript

