Problèmes liés au tri du code source v8 en JavaScript

Le vingtième et dernier article de la série de sujets JavaScript, interprétant le code source de tri de la v8

Avant-propos

la v8 est le moteur JavaScript de Chrome, qui contient des informations sur les tableaux Le tri est entièrement implémenté en JavaScript.

L'algorithme utilisé pour le tri est lié à la longueur du tableau. Lorsque la longueur du tableau est inférieure ou égale à 10, le tri par insertion est utilisé. Lorsque la longueur du tableau est supérieure à 10, le tri rapide est utilisé. . (Bien sûr, cette affirmation n’est pas rigoureuse).

Jetons d'abord un coup d'œil au tri par insertion et au tri rapide.

Tri par insertion

Principe

Considérez le premier élément comme une séquence ordonnée, parcourez le tableau et insérez les éléments suivants dans la séquence ordonnée construite.

Illustration

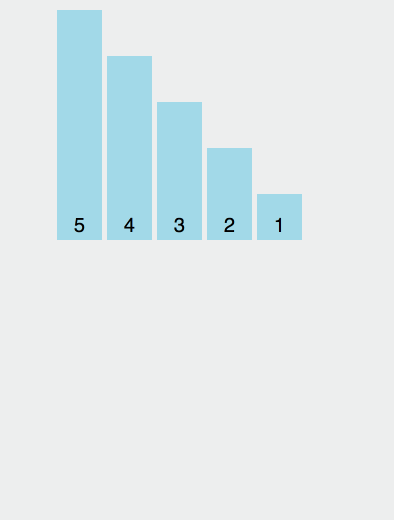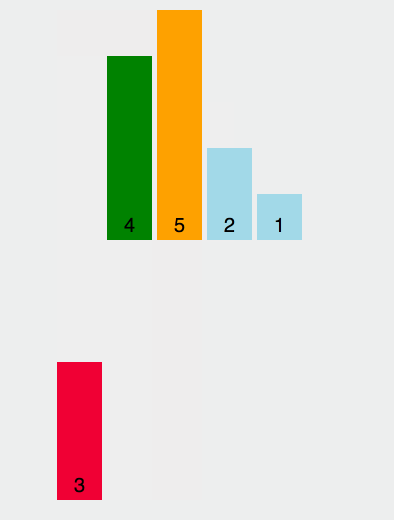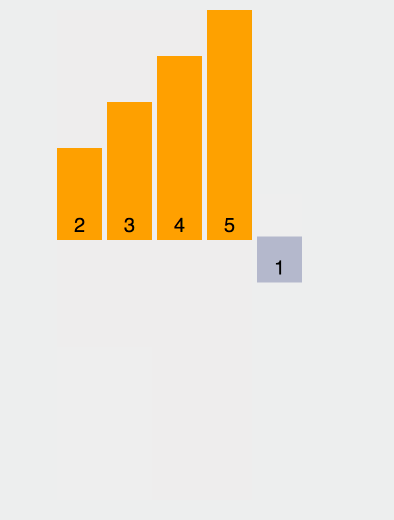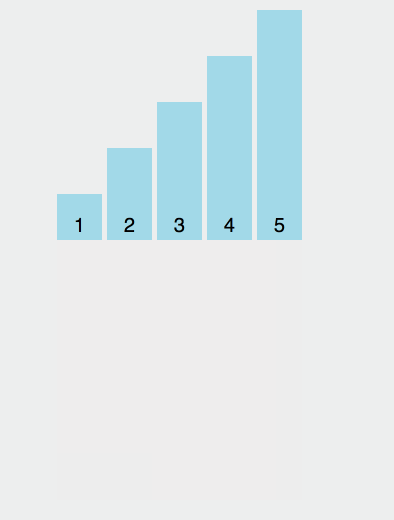
Mise en œuvre

function insertionSort(arr) {
    for (var i = 1; i < arr.length; i++) {
        var element = arr[i];
        for (var j = i - 1; j >= 0; j--) {
            var tmp = arr[j];
            var order = tmp - element;
            if (order > 0) {
                arr[j + 1] = tmp;
            } else {
                break;
            }
        }
        arr[j + 1] = element;
    }
    return arr;
}

var arr = [6, 5, 4, 3, 2, 1];
console.log(insertionSort(arr));

Complexité temporelle

Complexité temporelle Degré fait référence à l'effort de calcul requis pour exécuter l'algorithme. Il examine la situation où la taille de la valeur d'entrée approche l'infini. Généralement, le nombre de fois que les opérations de base de l'algorithme sont répétées est fonction de la taille du problème n.

Le meilleur des cas : le tableau est classé par ordre croissant, la complexité temporelle est : O(n)

Le pire des cas : le tableau est classé par ordre décroissant, la complexité temporelle est : O(n²)

Stabilité

La stabilité fait référence au fait de savoir si les mêmes éléments conservent leur position relative après le tri.

Il est à noter que pour les algorithmes de tri instables, il suffit de donner un exemple pour illustrer son instabilité tandis que pour les algorithmes de tri stables, l'algorithme doit être analysé pour obtenir des caractéristiques stables ;

Par exemple, [3, 3, 1], après le tri, est toujours [3, 3, 1], mais en réalité le deuxième 3 est avant le premier 3, alors c'est un algorithme de tri instable.

Le tri par insertion est un algorithme stable.

Avantages

Lorsque le tableau est sur le point d'être trié ou que la taille du problème est relativement petite, le tri par insertion est plus efficace. C'est pourquoi la v8 utilise le tri par insertion lorsque la longueur du tableau est inférieure ou égale à 10.

Tri rapide

Principe

1. Sélectionner un élément comme "base"

2. Moins de "base" " Les éléments plus grands que "base" sont déplacés vers la gauche de "base" ; les éléments plus grands que "base" sont déplacés vers la droite de "base".

3. Répétez les première et deuxième étapes pour les deux sous-ensembles à gauche et à droite de la "ligne de base" jusqu'à ce qu'il ne reste qu'un seul élément dans tous les sous-ensembles.

Exemple

L'exemple et l'implémentation suivante proviennent de "Implémentation Javascript du tri rapide" de l'enseignant Ruan Yifeng

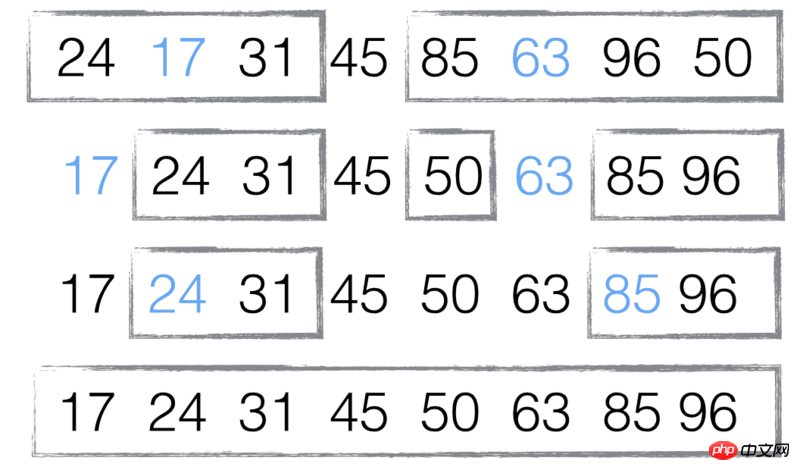
Avec tableau [ 85, 24, 63 , 45, 17, 31, 96, 50] Par exemple :

Dans un premier temps, sélectionnez l'élément du milieu 45 comme "base". (La valeur de base peut être choisie arbitrairement, mais choisir la valeur médiane est plus facile à comprendre.)

La deuxième étape, dans l'ordre, combinez chaque élément avec La « ligne de base » est comparée, formant deux sous-ensembles, l'un « inférieur à 45 » et l'autre « supérieur ou égal à 45 ».

La troisième étape consiste à répéter les première et deuxième étapes pour les deux sous-ensembles jusqu'à ce qu'il ne reste qu'un seul élément dans tous les sous-ensembles.

Implémentation

var quickSort = function(arr) {
　　if (arr.length <= 1) { return arr; }
    // 取数组的中间元素作为基准
　　var pivotIndex = Math.floor(arr.length / 2);
　　var pivot = arr.splice(pivotIndex, 1)[0];

　　var left = [];
　　var right = [];

　　for (var i = 0; i < arr.length; i++){
　　　　if (arr[i] < pivot) {
　　　　　　left.push(arr[i]);
　　　　} else {
　　　　　　right.push(arr[i]);
　　　　}
　　}
　　return quickSort(left).concat([pivot], quickSort(right));
};

Cependant, cette implémentation nécessite un espace supplémentaire pour stocker les sous-ensembles gauche et droit, il existe donc un autre Une mise en place du tri sur place.

Image

Regardons l'icône d'implémentation du tri sur place :

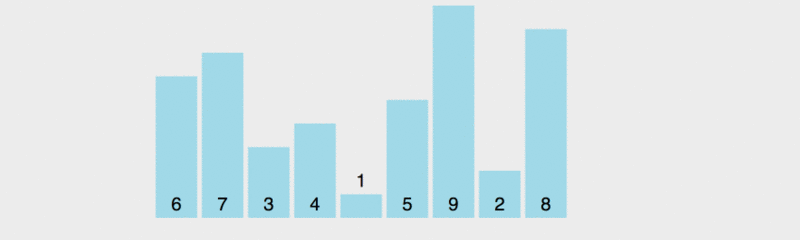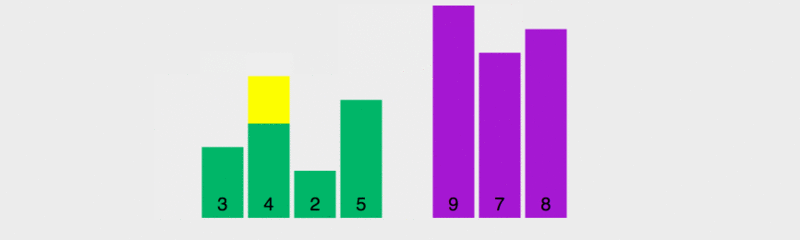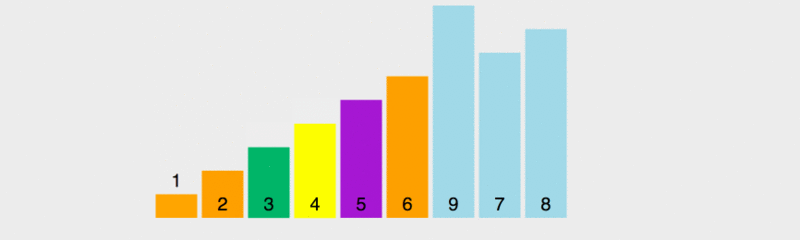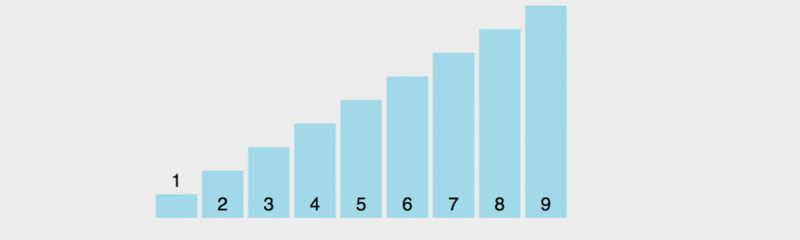
Dans l'ordre pour laisser tout le monde Après avoir compris le principe du tri rapide, j'ai ralenti la vitesse d'exécution.

Dans ce diagramme, la règle de valeur pour le benchmark est de prendre l'élément le plus à gauche. Le jaune représente le benchmark actuel, le vert représente les éléments qui sont plus petits que le benchmark et le violet représente les éléments qui sont supérieurs au benchmark.

Nous constaterons que l'élément vert sera immédiatement à droite du pivot, l'élément violet sera déplacé vers l'arrière, puis le pivot et le dernier élément vert seront échangés à ce moment-là, le pivot est dans la bonne position, c'est-à-dire que les éléments précédents sont tous inférieurs à la valeur de base et les éléments suivants sont tous supérieurs à la valeur de base. Prenez ensuite la base des multiples éléments précédents et suivants et triez-les.

Mise en œuvre sur place

function quickSort(arr) {
    // 交换元素
    function swap(arr, a, b) {
        var temp = arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }

    function partition(arr, left, right) {
        var pivot = arr[left];
        var storeIndex = left;

        for (var i = left + 1; i <= right; i++) {
            if (arr[i] < pivot) {
                swap(arr, ++storeIndex, i);
            }
        }

        swap(arr, left, storeIndex);

        return storeIndex;
    }

    function sort(arr, left, right) {
        if (left < right) {
            var storeIndex = partition(arr, left, right);
            sort(arr, left, storeIndex - 1);
            sort(arr, storeIndex + 1, right);
        }
    }

    sort(arr, 0, arr.length - 1);

    return arr;
}

console.log(quickSort(6, 7, 3, 4, 1, 5, 9, 2, 8))

Stabilité

Le tri rapide est un tri instable. Si l’on veut prouver qu’un tri est instable, il suffit de donner un exemple.

Alors donnons-en un~

就以数组 [1, 2, 3, 3, 4, 5] 为例，因为基准的选择不确定，假如选定了第三个元素(也就是第一个 3) 为基准，所有小于 3 的元素在前面，大于等于 3 的在后面，排序的结果没有问题。可是如果选择了第四个元素(也就是第二个 3 )，小于 3 的在基准前面，大于等于 3 的在基准后面，第一个 3 就会被移动到 第二个 3 后面，所以快速排序是不稳定的排序。

时间复杂度

阮一峰老师的实现中，基准取的是中间元素，而原地排序中基准取最左边的元素。快速排序的关键点就在于基准的选择，选取不同的基准时，会有不同性能表现。

快速排序的时间复杂度最好为 O(nlogn)，可是为什么是 nlogn 呢？来一个并不严谨的证明：

在最佳情况下，每一次都平分整个数组。假设数组有 n 个元素，其递归的深度就为 log₂n + 1，时间复杂度为 O(n)[(log₂n + 1)]，因为时间复杂度考察当输入值大小趋近无穷时的情况，所以会忽略低阶项，时间复杂度为：o(nlog₂n)。

如果一个程序的运行时间是对数级的，则随着 n 的增大程序会渐渐慢下来。如果底数是 10，lg1000 等于 3，如果 n 为 1000000，lgn 等于 6，仅为之前的两倍。如果底数为 2，log₂1000 的值约为 10，log₂1000000 的值约为 19，约为之前的两倍。我们可以发现任意底数的一个对数函数其实都相差一个常数倍而已。所以我们认为 O(logn)已经可以表达所有底数的对数了，所以时间复杂度最后为： O(nlogn)。

而在最差情况下，如果对一个已经排序好的数组，每次选择基准元素时总是选择第一个元素或者最后一个元素，那么每次都会有一个子集是空的，递归的层数将达到 n，最后导致算法的时间复杂度退化为 O(n²)。

这也充分说明了一个基准的选择是多么的重要，而 v8 为了提高性能，就对基准的选择做了很多优化。

v8 基准选择

v8 选择基准的原理是从头和尾之外再选择一个元素，然后三个值排序取中间值。

当数组长度大于 10 但是小于 1000 的时候，取中间位置的元素，实现代码为：

// 基准的下标
// >> 1 相当于除以 2 (忽略余数)
third_index = from + ((to - from) >> 1);

当数组长度大于 1000 的时候，每隔 200 ~ 215 个元素取一个值，然后将这些值进行排序，取中间值的下标，实现的代码为：

// 简单处理过
function GetThirdIndex(a, from, to) {
    var t_array = new Array();

    // & 位运算符
    var increment = 200 + ((to - from) & 15);

    var j = 0;
    from += 1;
    to -= 1;

    for (var i = from; i < to; i += increment) {
        t_array[j] = [i, a[i]];
        j++;
    }
    // 对随机挑选的这些值进行排序
    t_array.sort(function(a, b) {
        return comparefn(a[1], b[1]);
    });
    // 取中间值的下标
    var third_index = t_array[t_array.length >> 1][0];
    return third_index;
}

也许你会好奇 200 + ((to - from) & 15) 是什么意思？

& 表示是按位与，对整数操作数逐位执行布尔与操作。只有两个操作数中相对应的位都是 1，结果中的这一位才是 1。

以 15 & 127 为例：

15 二进制为： （0000 1111）

127 二进制为：（1111 1111）

按位与结果为：（0000 1111）＝ 15

所以 15 & 127 的结果为 15。

注意 15 的二进制为： 1111，这就意味着任何和 15 按位与的结果都会小于或者等于 15，这才实现了每隔 200 ~ 215 个元素取一个值。

v8 源码

终于到了看源码的时刻！源码地址为：https://github.com/v8/v8/blob/master/src/js/array.js#L758。

function InsertionSort(a, from, to) {
    for (var i = from + 1; i < to; i++) {
        var element = a[i];
        for (var j = i - 1; j >= from; j--) {
            var tmp = a[j];
            var order = comparefn(tmp, element);
            if (order > 0) {
                a[j + 1] = tmp;
            } else {
                break;
            }
        }
        a[j + 1] = element;
    }
};


function QuickSort(a, from, to) {

    var third_index = 0;
    while (true) {
            // Insertion sort is faster for short arrays.
        if (to - from <= 10) {
            InsertionSort(a, from, to);
            return;
        }
        if (to - from > 1000) {
            third_index = GetThirdIndex(a, from, to);
        } else {
            third_index = from + ((to - from) >> 1);
        }
        // Find a pivot as the median of first, last and middle element.
        var v0 = a[from];
        var v1 = a[to - 1];
        var v2 = a[third_index];

        var c01 = comparefn(v0, v1);
        if (c01 > 0) {
            // v1 < v0, so swap them.
            var tmp = v0;
            v0 = v1;
            v1 = tmp;
        } // v0 <= v1.
        var c02 = comparefn(v0, v2);
        if (c02 >= 0) {
            // v2 <= v0 <= v1.
            var tmp = v0;
            v0 = v2;
            v2 = v1;
            v1 = tmp;
        } else {
            // v0 <= v1 && v0 < v2
            var c12 = comparefn(v1, v2);
            if (c12 > 0) {
                // v0 <= v2 < v1
                var tmp = v1;
                v1 = v2;
                v2 = tmp;
            }
        }

        // v0 <= v1 <= v2
        a[from] = v0;
        a[to - 1] = v2;

        var pivot = v1;

        var low_end = from + 1; // Upper bound of elements lower than pivot.
        var high_start = to - 1; // Lower bound of elements greater than pivot.

        a[third_index] = a[low_end];
        a[low_end] = pivot;

        // From low_end to i are elements equal to pivot.
        // From i to high_start are elements that haven't been compared yet.

        partition: for (var i = low_end + 1; i < high_start; i++) {
            var element = a[i];
            var order = comparefn(element, pivot);
            if (order < 0) {
                a[i] = a[low_end];
                a[low_end] = element;
                low_end++;
            } else if (order > 0) {
                do {
                    high_start--;
                    if (high_start == i) break partition;
                    var top_elem = a[high_start];
                    order = comparefn(top_elem, pivot);
                } while (order > 0);

                a[i] = a[high_start];
                a[high_start] = element;
                if (order < 0) {
                    element = a[i];
                    a[i] = a[low_end];
                    a[low_end] = element;
                    low_end++;
                }
            }
        }


        if (to - high_start < low_end - from) {
            QuickSort(a, high_start, to);
            to = low_end;
        } else {
            QuickSort(a, from, low_end);
            from = high_start;
        }
    }
}

var arr = [10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0];

function comparefn(a, b) {
    return a - b
}

QuickSort(arr, 0, arr.length)
console.log(arr)

我们以数组 [10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0] 为例，分析执行的过程。

1.执行 QuickSort 函数 参数 from 值为 0，参数 to 的值 11。

2.10 c7ba78f8f51b7321cde06a9f72ed98cf> 1) = 5，基准值 a[5] 为 5。

3.比较 a[0] a[10] a[5] 的值，然后根据比较结果修改数组，数组此时为 [0, 9, 8, 7, 6, 5, 4, 3, 2, 1, 10]

4.将基准值和数组的第(from + 1)个即数组的第二个元素互换，此时数组为 [0, 5, 8, 7, 6, 9, 4, 3, 2, 1, 10]，此时在基准值 5 前面的元素肯定是小于 5 的，因为第三步已经做了一次比较。后面的元素是未排序的。

我们接下来要做的就是把后面的元素中小于 5 的全部移到 5 的前面。

5.然后我们进入 partition 循环，我们依然以这个数组为例，单独抽出来写个 demo 讲一讲

// 假设代码执行到这里，为了方便演示，我们直接设置 low_end 等变量的值
// 可以直接复制到浏览器中查看数组变换效果
var a = [0, 5, 8, 7, 6, 9, 4, 3, 2, 1, 10]
var low_end = 1;
var high_start = 10;
var pivot = 5;

console.log('起始数组为', a)

partition: for (var i = low_end + 1; i < high_start; i++) {

    var element = a[i];
    console.log('循环当前的元素为：', a[i])
    var order = element - pivot;

    if (order < 0) {
        a[i] = a[low_end];
        a[low_end] = element;
        low_end++;
        console.log(a)
    }
    else if (order > 0) {
        do {
            high_start--;
            if (high_start == i) break partition;
            var top_elem = a[high_start];
            order = top_elem - pivot;
        } while (order > 0);

        a[i] = a[high_start];
        a[high_start] = element;

        console.log(a)

        if (order < 0) {
            element = a[i];
            a[i] = a[low_end];
            a[low_end] = element;
            low_end++;
        }
        console.log(a)
    }
}

console.log('最后的结果为', a)
console.log(low_end)
console.log(high_start)

6.此时数组为 [0, 5, 8, 7, 6, 9, 4, 3, 2, 1, 10]，循环从第三个元素开始，a[i] 的值为 8，因为大于基准值 5，即 order > 0，开始执行 do while 循环，do while 循环的目的在于倒序查找元素，找到第一个小于基准值的元素，然后让这个元素跟 a[i] 的位置交换。
第一个小于基准值的元素为 1，然后 1 与 8 交换，数组变成  [0, 5, 1, 7, 6, 9, 4, 3, 2, 8, 10]。high_start 的值是为了记录倒序查找到哪里了。

7. À ce moment, la valeur de a[i] devient 1, puis échangez 1 avec la valeur de base 5. Le tableau devient [0, 1, 5, 7, 6, 9, 4, 3, 2, 8, 10] et la valeur de low_end est augmentée de 1. La valeur de low_end est d'enregistrer l'emplacement de la valeur de base.

8. La boucle est ensuite exécutée en parcourant le quatrième élément 7, ce qui est cohérent avec les étapes 6 et 7. Le tableau devient d'abord [0, 1, 5, 2, 6, 9, 4, 3, 7, 8, 10], puis devient [0, 1, 2, 5, 6, 9, 4, 3, 7, 8, 10]

9. . Parcourez le cinquième élément 6, comme pour les étapes 6 et 7. Le tableau devient d'abord [0, 1, 2, 5, 3, 9, 4, 6, 7, 8, 10], puis [0, 1, 2, 3, 5, 9, 4, 6, 7, 8, 10]

10. Parcourez le sixième élément 9, suivez les étapes 6 et 7. Les étapes sont identiques, le tableau devient d'abord [0, 1, 2, 3, 5, 4, 9, 6, 7, 8, 10], puis devient [0, 1, 2, 3, 4, 5, 9, 6, 7, 8, 10]

11 lors du prochain parcours, car i == high_start, cela signifie que les recherches avant et arrière sont finalement trouvées ensemble, Les éléments suivants sont nettement supérieurs à la valeur de base. A ce moment, quittez la boucle

12. Le résultat après parcours est [0, 1, 2, 3, 4, 5, 9, 6, 7, 8, 10] Les éléments devant la valeur de base 5 sont tous inférieurs à 5, et les éléments suivants sont tous supérieurs à 5. Ensuite, nous effectuons QuickSort

13 sur les deux sous-ensembles respectivement. À ce stade, la valeur low_end est 5, la valeur high_start est 6, la valeur de to est toujours 10. , la valeur de from est toujours 0, et le résultat de to - high_start < low_end - from est true, nous trions QuickSort(a, 6, 10), c'est-à-dire trions les éléments suivants, mais notons que dans le nouveau QuickSort, car le la valeur de - à est inférieure à 10, le tri par insertion est en fait utilisé cette fois. Donc pour être précis, lorsque la longueur du tableau est supérieure à 10, la v8 utilise une méthode de tri hybride de tri rapide et de tri par insertion.

14. Ensuite, to = low_end prend la valeur 5. En raison de while(true), il sera à nouveau exécuté. La valeur de to - from est 5 et InsertionSort(a, 0, 5 est. exécuté. ), c’est-à-dire effectuer un tri par insertion sur l’élément avant la valeur de référence.

15. Parce qu'il y a une instruction return dans le jugement de to - from <= 10, la boucle while se termine.

16.v8 Après avoir effectué un tri rapide sur le tableau, puis effectué un tri par insertion sur les deux sous-ensembles respectivement, et enfin modifié le tableau en un tableau correctement trié.

Comparaison

Enfin, prenons un diagramme schématique pour expérimenter le tri par insertion et le tri rapide :

Le l'image provient de https ://www.toptal.com/developers/sorting-algorithms

Special Series

Adresse du répertoire JavaScript Special Series : https://github.com/mqyqingfeng/Blog.

La série de sujets JavaScript devrait comprendre une vingtaine d'articles, étudiant principalement l'implémentation de certains points fonctionnels dans le développement quotidien, tels que l'anti-shake, la limitation, la déduplication, le jugement de type, la copie, la valeur maximale, l'aplatissement, curry, récursivité, réorganisation, tri, etc. se caractérisent par l'étude (chao) de l'implémentation du soulignement et de jQuery.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!