Maison >développement back-end >Tutoriel Python >Un exemple explique comment Python implémente la fonction de parcours graphique basée sur le modèle d'arborescence de sous-ensemble de méthode de backtracking.
Un exemple explique comment Python implémente la fonction de parcours graphique basée sur le modèle d'arborescence de sous-ensemble de méthode de backtracking.
- 巴扎黑original
- 2017-09-07 10:14:571832parcourir
Cet article présente principalement la fonction de parcours de graphe de Python basée sur le modèle d'arbre de sous-ensemble de méthode de retour en arrière, et analyse les compétences opérationnelles et les précautions associées de Python en utilisant le modèle d'arbre de sous-ensemble de méthode de retour en arrière pour les problèmes de parcours de graphe sous forme d'exemples. qui en a besoin peut Pour référence,
Cet article décrit l'exemple de Python implémentant la fonction de traversée de graphe basée sur le modèle d'arborescence de sous-ensemble de méthode de backtracking. Partagez-le avec tout le monde pour votre référence, les détails sont les suivants :
Question
Une photo :
A - ->B
A --->C
C --> 🎜>C - -> D
D ---> d'après l'image Partant d'un nœud E, après avoir traversé tous les autres nœuds sans répétition, il revient au nœud de départ E, qui est appelé un chemin. Veuillez trouver tous les chemins possibles.
Analyse
Cette question concerne Graphique, nous devons alors d’abord considérer par quel type de structure de stockage le graphique est représenté. Les matrices de contiguïté, les listes de contiguïté,... ne sont pas très familières. L'article précédent http://www.jb51.net/article/122927.htm a la représentation de liste de contiguïté la plus simple.
Ensuite, analysez le problème lui-même :
Évidemment, la longueur de la solution au problème est fixe, c'est-à-dire que toutes les longueurs de chemin sont fixes : n (sans revenir au nœud de départ) Soit n+1 (retour au nœud de départ) 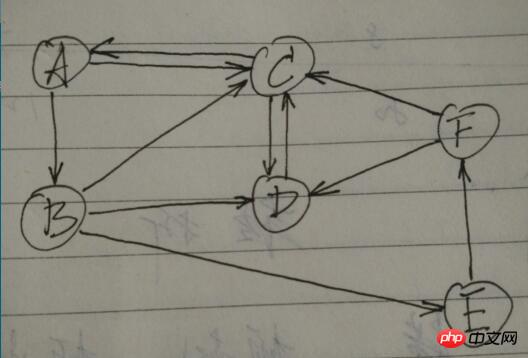
Code :
Rendu :
'''
图的遍历
从一个节点出发,不重复地经过所有其它节点后,回到出发节点。找出所有的路径
'''
# 用邻接表表示图
n = 6 # 节点数
a,b,c,d,e,f = range(n) # 节点名称
graph = [
{b,c},
{c,d,e},
{a,d},
{c},
{f},
{c,d}
]
x = [0]*(n+1) # 一个解(n+1元数组,长度固定)
X = [] # 一组解
# 冲突检测
def conflict(k):
global n,graph,x
# 第k个节点,是否前面已经走过
if k < n and x[k] in x[:k]:
return True
# 回到出发节点
if k == n and x[k] != x[0]:
return True
return False # 无冲突
# 图的遍历
def dfs(k): # 到达(解x的)第k个节点
global n,a,b,c,d,e,f,graph,x,X
if k > n: # 解的长度超出,已走遍n+1个节点 (若不回到出发节点,则 k==n)
print(x)
#X.append(x[:])
else:
for node in graph[x[k-1]]: # 遍历节点x[k]的邻接节点(x[k]的所有状态)
x[k] = node
if not conflict(k): # 剪枝
dfs(k+1)
# 测试
x[0] = e # 出发节点
dfs(1) # 开始处理解x中的第2个节点Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

