Maison >Java >javaDidacticiel >Explication détaillée des opérations binaires et binaires en Java
Explication détaillée des opérations binaires et binaires en Java
- 零下一度original
- 2017-07-16 16:58:514132parcourir
1. Méthode de représentation :
Dans le langage Java, les nombres binaires sont représentés en complément à deux, le bit le plus élevé est le bit de signe, le bit de signe des nombres positifs est 0, et le bit de signe des nombres négatifs est 1. La représentation du code complément doit répondre aux exigences suivantes.
(1) Le bit le plus élevé d'un nombre positif est 0, et les bits restants représentent la valeur elle-même (nombre binaire).
(2) Pour un nombre négatif, le complément de la valeur absolue du nombre est inversé au niveau du bit, puis 1 est ajouté au nombre entier.
Opérations au niveau du bitExpression se compose d'opérandes et d'opérateurs au niveau du bit, implémentant le type entierEffectuer au niveau du bit opérations sur les nombres binaires. Les opérateurs de bits peuvent être divisés en opérateurs logiques (y compris ~, &, | et ^) et en opérateurs de décalage (y compris >>, << et >>>).
1) L'opérateur de décalage gauche (<<) peut déplacer l'opérande du côté gauche de l'opérateur vers la gauche du nombre de chiffres spécifié sur le côté droit de l'opérateur (en remplissant 0 dans le peu faible).
2) L'opérateur de décalage vers la droite "signé" (>>) déplace l'opérande du côté gauche de l'opérateur vers la droite du nombre de chiffres spécifié sur le côté droit de l'opérateur. L'opérateur de décalage à droite « signé » utilise « l'extension de signe » : si la valeur est positive, 0 est inséré dans le bit haut ; si la valeur est négative, 1 est inséré dans le bit haut.
3) Java a également ajouté un opérateur de décalage vers la droite "non signé" (>>>), qui utilise "l'extension zéro": qu'il soit positif ou négatif, des 0 sont insérés dans le haut morceaux. Cet opérateur n'est pas disponible en C ou C++.
4) Si char, byte ou short sont décalés, ils seront automatiquement convertis en int avant que le décalage ne soit effectué. Seuls les 5 bits bas à droite sont utilisés. Cela nous empêche de déplacer un nombre irréaliste de chiffres dans un int. Si une valeur longue est traitée, le résultat final obtenu est également long. A ce moment, seuls les 6 bits faibles à droite seront utilisés pour empêcher le mouvement de dépasser le nombre de chiffres prêts à l'emploi dans la valeur longue. Mais vous pouvez également rencontrer un problème lors de l'exécution de décalages à droite « non signés ». Si vous effectuez une opération de décalage vers la droite sur un octet ou une valeur courte, le résultat peut ne pas être correct (en particulier Java 1.0 et Java 1.1). Ils sont automatiquement convertis en type int et décalés vers la droite. Mais "une extension nulle" ne se produit pas, vous obtenez donc un résultat de -1 dans ces cas.
Le binaire est un système numérique largement utilisé en technologie informatique. Les données binaires sont un nombre représenté par deux chiffres, 0 et 1. Sa base est 2, la règle de report est « tous les deux sont transmis à un » et la règle d'emprunt est « emprunter un pour être égal à deux », découverte par Leibniz, le maître allemand de philosophie mathématique au XVIIIe siècle. Le système informatique actuel utilise essentiellement un système binaire et les données sont principalement stockées dans l'ordinateur sous la forme d'un code complémentaire à deux. Le système binaire de l'ordinateur est un tout petit interrupteur, « on » représentant 1 et « off » représentant 0.
Alors, à quoi ressemble le binaire en Java ? Découvrons ensemble son voile mystérieux.
1. La conversion décimale intégrée à Java
Les méthodes de calcul de base pour la conversion de décimal en binaire et la conversion de binaire en décimal ne seront pas abordées ici. .
Il existe plusieurs méthodes intégrées à Java pour nous aider à convertir diverses bases. Comme le montre la figure ci-dessous (en prenant la mise en forme d'entiers comme exemple, les autres types sont les mêmes) :
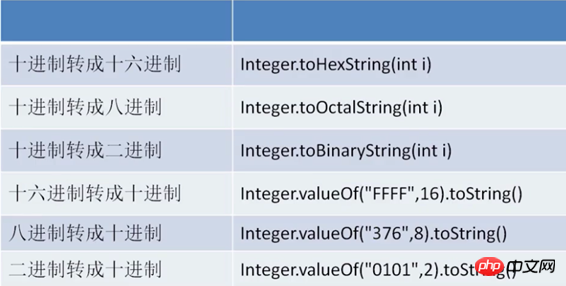
1, convertissez le nombre décimal en d'autres bases :
1 二进制:Integer.toHexString(int i);2 八进制:Integer.toOctalString(int i);3 十六进制:Integer.toBinaryString(int i);
2. Convertissez d'autres bases en décimales :
1 二进制:Integer.valueOf("0101",2).toString;2 八进制:Integer.valueOf("376",8).toString;3 十六进制:Integer.valueOf("FFFF",16).toString;
3 Utilisez la méthode parseInt() et la méthode valueOf() dans la classe Integer pour convertir d'autres bases. en décimal.
La différence est que la valeur de retour de la méthode parseInt() est de type int, tandis que la valeur de retour de valueOf() est un objet Integer.
2. Opérations binaires de base
Le binaire peut additionner, soustraire, multiplier et diviser tout comme le décimal, mais il a également une méthode de fonctionnement plus simple : les opérations sur les bits. Par exemple, la taille du type int dans les ordinateurs est de 32 bits, qui peuvent être représentés par des nombres binaires de 32 bits, nous pouvons donc utiliser des opérations sur bits pour calculer les valeurs du type int. Bien sûr, vous pouvez également utiliser des méthodes ordinaires pour en calculer certaines. données, je vous présente ici principalement les méthodes d'opérations sur les bits. Nous constaterons que les opérations sur bits ont une puissance incomparable avec les méthodes d'opération ordinaires. Pour plus d'applications d'opérations sur bits, veuillez passer à mon prochain article de blog "Opérations sur bits magiques"
Tout d'abord, jetons un coup d'œil aux opérateurs de base d'opérations sur bits :
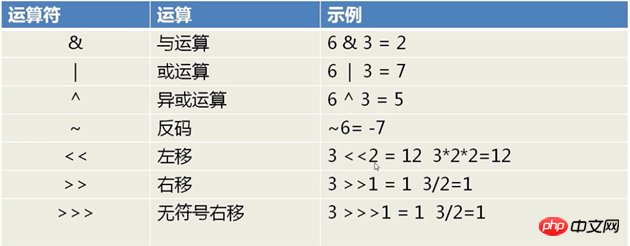
Avantages :
Dans certaines circonstances, calcul facile, vitesse rapide, large support
Si vous utilisez des méthodes arithmétiques, c'est lent et la logique est compliquée
Les opérations au niveau des bits ne se limitent pas à une seule langue, c'est la méthode de fonctionnement de base des ordinateurs
>>> >>>>>>>>>>>>>>>>>>> >>>>>>>>>>>>>>>>>>> >
(1) AND au niveau du bit &
Si les deux bits sont 1, le résultat est 1
0&0=0; 0&1= 0;1&0=0;1&1=1
Par exemple : 51&5 est 0011 0011 & 0000 0101 =0000 0001 donc 51&5=1.
Utilisation particulière
(1)Effacer. Si vous souhaitez remettre une unité à zéro, même si tous ses bits binaires sont 0, il suffit de la ET avec une valeur dont les bits sont tous nuls, et le résultat sera zéro.
(2) Prendre la position spécifiée dans un nombre.
Par exemple : Supposons que X=10101110, prenons les quatre chiffres inférieurs de X et utilisons
Méthode : Trouver un nombre qui correspond au bit que x doit être. Le bit correspondant du nombre est 1 et les bits restants sont zéro. Effectuez une opération ET sur ce nombre et x pour obtenir le spécifié. peu en x.
(2) OU au niveau du bit |
Tant que l'un d'eux vaut 1, le résultat est 1.
0|0=0; 0|1=1; 1|0=1;
Par exemple : 51|5 qui est 0011 0011 | 0000 0101 =0011 0111 Par conséquent 51|5=55
L'usage spécial
est souvent utilisé pour définir 1 sur certaines positions de dans une donnée .
Méthode : Trouver un nombre correspondant au bit de x à mettre à 1. Le bit correspondant du nombre est 1 et les bits restants sont zéro. Ce nombre est relatif à x ou définit une position dans x sur 1.
(3) OU exclusif^
Si les deux bits correspondants sont "exclusifs" (valeurs différentes), alors le résultat du bit est 1, sinon il est 0
0^0=0; 0^1=1; 1^0=1; 1^1=0;
Par exemple : 51^5 est 0011 0011 ^ 0000 0101 = 0011 0110 donc 51^ 5=54
Usage spécial
(1) est en OU exclusif avec 1, retourne un spécifique bit
Méthode : Trouver un nombre qui correspond au bit dans
Par exemple : X=1010 1110, retournez les quatre bits inférieurs de
(2) OU exclusif avec 0, conserver la valeur d'origine
Par exemple : >Deux variables échangent des valeurs
1 . Utilisez la troisième variable pour réaliser
C=A;A=B;B=C;2 Utilisez l'addition et la soustraction pour réaliser l'échange de deux variables . A=A+B;B=A-B;A=A-B;3. Utilisez l'opération XOR au niveau du bit pour y parvenir, qui est également le plus efficacePrincipe : Le XOR de un nombre est lui-même égal à 0 ; ^B;A=A^B
(4) Négation et opération~Inverser un nombre binaire au niveau du bit, c'est-à-dire changer 0 en 1 et 1 en 0
~1=0; ~0=1(5) Décalage vers la gauche<<
Décaler tous les bits binaires d'un opérande à gauche d'un certain nombre de bits (le bit binaire à gauche est ignoré et 0 est ajouté à droite)
Par exemple : 2<<1 =4 10<<1=100
Le bit haut supprimé lors du décalage vers la gauche Si 1 n'est pas inclus, chaque décalage vers la gauche équivaut à multiplier le nombre par 2.Par exemple :
11(1011)<<2= 0010 1100=22
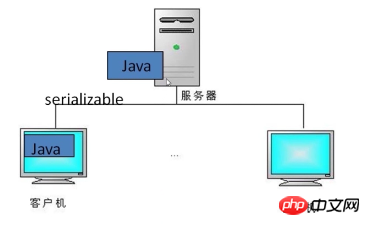
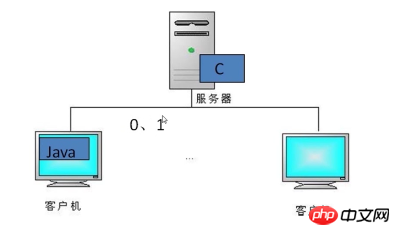
11(00000000 00000000 00000000 1011) 32 bits Décalez tous les chiffres binaires d'un nombre vers la droite d'un certain nombre de places, complétez la gauche avec 0 pour les nombres positifs, complétez la gauche avec 1 pour les nombres négatifs , et jetez le droit. Si le bit de poids fort n'est pas 1 (c'est-à-dire qu'il ne s'agit pas d'un nombre négatif) lors du décalage vers la droite, chaque fois que l'opérande est décalé vers la droite, cela équivaut à diviser le nombre par 2. Le remplissage à gauche avec 0 ou avec 1 dépend du fait que le nombre déplacé est positif ou négatif. Par exemple : 4>>2=4/2/2=1 -14 (soit 1111 0010)>>2 =1111 1100=-4 Décalage chaque bit vers la droite du nombre de chiffres spécifié,Après le décalage à droite, les bits libérés à gauche sont remplis de zéros, retirez le bon bit et jetez-le. Par exemple : -14>>>2 (c'est-à-dire 11111111 11111111 11111111 11110010)>>>2 = (00111111 11111111 11111111 11111100)=1073741820 >>>>>>>>>> ;& gt; > ;>>>>>>>>>>>>>>>>>>>>>>>> > ;>>>>>>>>>>>>>>>>> mentionné ci-dessus La représentation binaire d'un nombre négatif est légèrement différente de celle d'un nombre positif, de sorte que l'opération au niveau du bit est également différente de celle d'un nombre positif. Un nombre négatif s'exprime sous sa forme complémentaire comme un nombre positif ! Prenons le -14 mentionné ci-dessus comme exemple pour expliquer brièvement le code original, le code inverse et le code complémentaire. Code original Un nombre binaire converti à partir d'un entier selon sa valeur absolue est appelé le code original Pour exemple : 00000000 00000000 00000000 00001110 est le code original de 14. Code inverse Inversez le nombre binaire petit à petit, et le nouveau nombre binaire résultant est appelé l'inverse de l'original code numérique binaire. Par exemple : annulez chaque bit de 00000000 00000000 00000000 00001110, obtient 11111111 11111111 11111111 0001 Remarque : Ces deux-là sont complémentaires l'un de l'autre code complémentaire Le complément plus 1 s'appelle le complément 11111111 11111111 11110001 +1= 11111111 11111111 11111111 11110010 Maintenant, nous obtenons la représentation binaire de -14, maintenant décalez-la vers la gauche de -14 (11111111 11111111 11111111 11110010)<<2 = 11111111 11111111 11111111 11001000 =? Analyse : Le premier bit de ce nombre binaire est 1, indiquant qu'il est sous forme de complément à deux. Nous devons maintenant convertir le code du complément en code d'origine (sa valeur positive) et convertir le code original en code complément à deux Au contraire, les étapes pour convertir le code complément en code original : Le code complément est soustrait par 1 pour obtenir le code complément : (11000111) Les 24 premiers bits sont 1, et Inversez le code pour obtenir le code d'origine (c'est-à-dire la valeur positive du nombre négatif) (00111000) Calculez la valeur positive, la valeur positive est 56 Prenez l'opposé de la valeur positive et obtenez le résultat -56 Conclusion : -14<<2 = -56 Le binaire est-il beaucoup utilisé en Java ? Dans le développement quotidien, la « conversion de base » et les « opérations sur les bits » ne sont pas beaucoup utilisées. Java gère les tâches de haut niveau. est souvent utilisé en multiplateforme, comme : la lecture et l'écriture de fichiers, la communication de données. Regardons un scénario : Si le client et le serveur sont tous deux des programmes écrits en langage Java, alors lorsque le client envoie des données d'objet, nous Les données à envoyer peuvent être sérialisées en sérialisables. Une fois que le serveur a obtenu les données sérialisées, il peut les désérialiser et lire les données de l'objet qu'elles contiennent. À mesure que le nombre de visites de clients augmente, nous ne prenons pas en compte les performances du serveur. En fait, une solution réalisable consiste à changer le langage Java du serveur en langage C. Le langage C, en tant que langage sous-jacent, reflète plus rapidement que le langage Java. Si le client transmet des données sérialisées à ce moment-là, le langage C côté serveur ne pourra pas les analyser. Nous pouvons convertir les données en binaire (0,1) afin que le serveur puisse analyser ces langues. >>>>>>>>>>>>> ;>> ;>>>>>>>>>>>>>>>>>>>>>>>>> ;>>>>>>>>>>>> types de données de base en JavaIl existe les quatre types suivants : Type de données Int : octet (8 bits, -128~127), court (16 bits), int (32 bits), long (64 bits) Type de données float : simple précision (float, 32 bits), double précision (double, 64 bits) Les valeurs des variables de type booléen sont vraies et fausses (Les deux sont de 1 bit) type de données char : caractère unicode, 16 bits type de classe correspondant : Integer, Float , Booléen, Caractère, Double, Court, Octet, Long ;>>>>>>>>>>>>>>>>>>> ;>>>>>> ;>>>>>>>>>>>>>>>> (1) Type de données Convertir en octetsPar exemple : type int 8143 (00000000 00000000 00011111 11001111) Premier octet (bas de gamme) : 8143>>0*8 & 0xff=(11001111)=207 (ou signé -49) Deuxième (bas fin) octet : 8143> ;>1*8 &0xff=(00011111)=31 Troisième octet (bas de gamme) : 8143>>2*8 &0xff=00000000=0 Quatrième octets (bas de gamme) : 8143>>3*8 &0xff=00000000=0 Nous avons remarqué que ce qui précède (bas de gamme) commence de droite à gauche, et alors ? C'est du bas de gamme ? Expliquons-le du point de vue du grand et du petit endian. Les octets faibles sont disposés à l'extrémité de l'adresse de la mémoire. de cette valeur, l'octet haut est classé à l'extrémité de l'adresse haute de la mémoireBig-Endian L'octet haut est disposé à l'extrémité de l'adresse de la mémoire, qui est l'adresse de départ de la valeur, et l'octet bas est classé dans le hauteadresse fin de la mémoire En effet, dans les systèmes informatiques, nous utilisons les octets comme unités. Chaque unité d'adresse correspond à un octet, et un octet est composé de 8 bits. Cependant, dans le langage C , en plus du caractère 8 bits, il existe également un type court de 16 bits et un type long de 32 bits (selon le compilateur spécifique). De plus, pour les chiffres supérieurs à Pour les processeurs 8 bits, tels que les processeurs 16 bits ou 32 bits, puisque la largeur du registre est supérieure à un octet, il doit y avoir un problème d'organisation de plusieurs octets. Cela conduit au mode de stockage big-endian et au mode de stockage small-endian. Par exemple, un type court de 16 bits x, l'adresse dans la mémoire est 0x0010 et la valeur de x est 0x1122, alors 0x11 est l'octet de poids fort et 0x22 est l'octet de poids faible. Pour le mode big-endian, mettez 0x11 dans l'adresse basse, c'est-à-dire 0x0010, et 0x22 dans l'adresse haute, c'est-à-dire 0x0011. Le mode Little Endian est tout le contraire. Notre structure X86 couramment utilisée est le mode Little Endian, tandis que KEIL C51 est le mode Big Endian. De nombreux ARM et DSP sont en mode petit-boutiste. Certains processeurs ARM peuvent également sélectionner le mode big-endian ou little-endian par matériel. Par exemple : numéro 32 bits 0x12 34 56 78 (hexadécimal) La méthode de stockage du CPU en mode Big-Endian (en supposant qu'il démarre à partir de l'adresse 0x4000) est 0x4000 0x4001 0x4002 0x4003 存放内容 0x78 0x56 0x34 0x12 在Little-Endian模式CPU的存放方式(假设从地址0x4000开始存放)为 内存地址 0x4000 0x4001 0x4002 0x4003 存放内容 0x12 0x34 0x56 0x78 1.字符串->字节数组 2.字节数组->字符串 >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> 两种类型转化为字节的方法都介绍了,下面写个小例子检验一下: 运行结果: 结束语:最近偷懒了,没有好好学习,好几天没写文了,哎,还请大家多多监督! Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois! (6) Décalage vers la droite>>
(7) Opération de décalage à droite non signée>>>
Trois, Arithmétique de base en Java
=>byte[] b=[-49 ,31,0,0]
Adresse mémoire
(二)字符串转化为字节
1 String s;2 byte[] bs=s.getBytes();
1 Byte[] bs=new byte[int];2 String s =new String(bs);或3 String s=new String(bs,encode);//encode指编码方式,如utf-8
1 public class BtyeTest { 2 /* 3 * int整型转为byte字节 4 */ 5 public static byte[] intTOBtyes(int in){ 6 byte[] arr=new byte[4]; 7 for(int i=0;i<4;i++){ 8 arr[i]=(byte)((in>>8*i) & 0xff); 9 }10 return arr;11 }12 /*13 * byte字节转为int整型14 */15 public static int bytesToInt(byte[] arr){16 int sum=0;17 for(int i=0;i<arr.length;i++){18 sum+=(int)(arr[i]&0xff)<<8*i;19 }20 return sum;21 }22 public static void main(String[] args) {23 // TODO Auto-generated method stub24 byte[] arr=intTOBtyes(8143);25 for(byte b:arr){26 System.out.print(b+" ");27 }28 System.out.println();29 System.out.println(bytesToInt(arr));30 31 //字符串与字节数组32 String str="云开的立夏de博客园";33 byte[] barr=str.getBytes();34 35 String str2=new String(barr);36 System.out.println("字符串转为字节数组:");37 for(byte b:barr){38 System.out.print(b+" ");39 40 }41 System.out.println();42 43 System.out.println("字节数组换位字符串:"+str2);44 45 46 }47 48 }


