Liste de contiguïté de conception de table de base de données, énumération de chemin, ensemble imbriqué, table de fermeture

Lorsque nous concevrons la base de données, allons-nous briser les conventions et trouver la solution de conception qui correspond le mieux à nos besoins :

Liste de contiguïté couramment utilisée ? design , un champ parent_id sera ajouté, tel qu'une table régionale (pays, province, ville, district) :

CREATE TABLE Area ([id] [int]  NOT NULL,[name] [nvarchar]  (50) NULL,[parent_id] [int]  NULL,[type] [int]  NULL );

name : le nom de la région, parent_id est l'ID parent, l'ID parent de la province est le pays, l'ID parent de la ville est la province, et ainsi de suite.

type est le niveau de la région : 1 : pays, 2 : province, 3 : ville, 4 : district

est relativement certain au niveau Dans ce cas, il n'y a aucun problème à concevoir le tableau comme celui-ci, et il est également très pratique d'appeler.

Cependant, l'utilisation de cette méthode de conception de liste de contiguïté ne peut pas répondre à tous les besoins. Lorsque nous ne sommes pas sûrs du niveau, supposons que j'ai la structure de commentaire suivante :

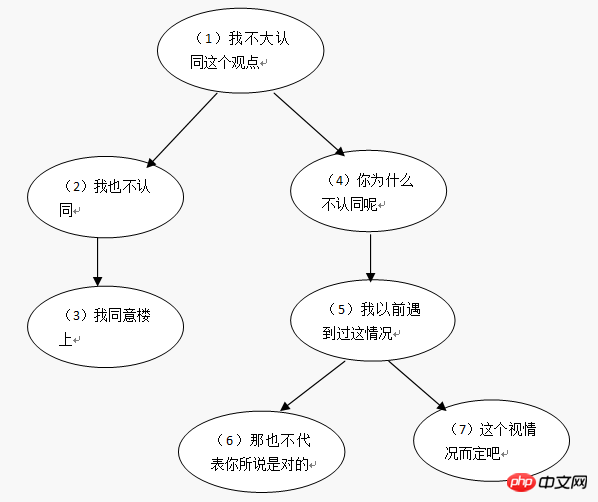
Utiliser une liste de contiguïté pour enregistrer les données de ce commentaire (table des commentaires) :

comment_id	parent_id	author	comment
1	0	小明	我不大认同这个观点
2	1	小张	我也不认同
3	2	小红	我同意楼上
4	1	小全	你为什么不认同呢
5	4	小明	我以前遇到过这情况
6	5	小张	那也不代表你所说是对的
7	5	小新	这个视情况而定吧

Avez-vous déjà remarqué qu'avec une telle conception de table, il est difficile d'interroger tous les descendants d'un nœud. Vous pouvez utiliser des requêtes associées pour obtenir un commentaire et ses descendants :

SELECT c1.*, c2.* FROM comments c1 LEFT OUTER JOIN comments c2 ON c2.parent_id = c1.comment_id;

Cependant, cette requête ne peut obtenir que deux niveaux de données. La caractéristique de ce type d’arbre est qu’il peut être étendu à n’importe quelle profondeur et que vous devez disposer d’une méthode correspondante pour obtenir ses données de profondeur. Par exemple, vous devrez peut-être compter le nombre de branches de commentaires ou calculer le coût total d’une machine.

Dans certains cas, utiliser des listes de contiguïté dans les projets est parfait. L'avantage de la conception de liste de contiguïté est qu'elle peut obtenir rapidement les nœuds parents et enfants directs d'un nœud donné, et qu'elle peut également facilement insérer de nouveaux nœuds. Si une telle exigence concerne toutes les opérations de votre projet sur des données hiérarchiques, alors l'utilisation de listes de contiguïté fonctionnera bien.

Lorsque vous rencontrez le modèle d'arbre ci-dessus, plusieurs options peuvent être envisagées : l'énumération des chemins, les ensembles imbriqués et les tables de fermeture. Ces solutions semblent souvent beaucoup plus complexes que les listes de contiguïté, mais elles facilitent certaines opérations qui seraient compliquées ou inefficaces pour utiliser des listes de contiguïté. Si votre projet doit réellement fournir ces opérations, ces conceptions constitueraient un meilleur choix pour les listes de contiguïté.

1. Énumération du chemin

Dans la table des commentaires, nous utilisons le champ chemin de type varchar pour remplacer le champ parent_id d'origine. Le contenu stocké dans ce champ de chemin est la séquence depuis l'ancêtre de niveau supérieur du nœud actuel jusqu'à sa propre séquence. Tout comme le chemin UNIX, vous pouvez même utiliser '/' comme séparateur de chemin.

 

      你可以通过比较每个节点的路径来查询一个节点祖先。比如：要找到评论#7， 路径是 1/4/5/7一 的祖先，可以这么做：

SELECT * FROM comments AS c WHERE '1/4/5/7' LIKE c.path || '%' ;

    这句话查询语句会匹配到路径为 1/4/5/%，1/4/% 以及 1/% 的节点，而这些节点就是评论#7的祖先。

 

    同时还可以通过将LIKE 关键字两边的参数互换，来查询一个给定节点的所有后代。比如查询评论#4，路径path为 ‘1/4’ 的所有后代，可以使用如下语句：

SELECT * FROM comemnts AS c WHERE c.path LIKE '1/4' || '%' ;

    这句查询语句所有能找到的后台路径分别是：1/4/5、1/4/5/6、1/4/5/7。

 

     一旦你可以很简单地获取一棵子树或者从子孙节点到祖先节点的路径，你就可以很简单地实现更多的查询，如查询一颗子树所有节点上值的总和。

插入一个节点也可以像使用邻接表一样地简单。你所需要做的只是复制一份要插入节点的父亲节点路径，并将这个新节点的ID追加到路径末尾即可。

 

     路径枚举也存在一些缺点，比如数据库不能确保路径的格式总是正确或者路径中的节点确实存在。依赖于应用程序的逻辑代码来维护路径的字符串，并且验证字符串的正确性开销很大。无论将varchar 的长度设定为多大，依旧存在长度的限制，因而并不能够支持树结构无限扩展。

 

二、 嵌套集

 

     嵌套集解决方案是存储子孙节点的相关信息，而不是节点的直接祖先。我们使用两个数字来编码每个节点，从而表示这一信息，可以将这两个数字称为nsleft 和 nsright。

每个节点通过如下的方式确定nsleft 和nsright 的值：nsleft的数值小于该节点所有后代ID，同时nsright 的值大于该节点的所有后代的ID。这些数字和comment_id 的值并没有任何关联。

     确定这三个值（nsleft，comment_id，nsright）的简单方法是对树进行一次深度优先遍历，在逐层深入的过程中依次递增地分配nsleft的值，并在返回时依次递增地分配nsright的值。得到数据如下:

 

 

comment_id	nsleft	nsright	author	comment
1	1	14	小明	我不大认同这个观点
2	2	5	小张	我也不认同
3	3	4	小红	我同意楼上
4	6	13	小全	你为什么不认同呢
5	7	12	小明	我以前遇到过这情况
6	8	9	小张	那也不代表你所说是对的
7	10	11	小新	这个视情况而定吧

       一旦你为每个节点分配了这些数字，就可以使用它们来找到指定节点的祖先和后代。比如搜索评论#4及其所有后代，可以通过搜索哪些节点的ID在评论 #4 的nsleft 和 nsright 范围之间，例：

SELECT c2.* FROM comments AS c1 JOIN comments AS c2 ON c2.nsleft BETWEEN c1.nsleftAND c1.nsright WHERE c1.comment_id = 4;

比如搜索评论#6及其所有祖先，可以通过搜索#6的ID在哪些节点的nsleft 和 nsright 范围之间，例：

SELECT c2.* FROM comments AS c1 JOIN comments AS c2 ON c1.nsleft BETWEEN c2.nsleftAND c2.nsright WHERE c1.comment_id = 6;

     使用嵌套集设计的主要优势是，当你想要删除一个非叶子节点时，它的后代会自动替代被删除的节点，成为其直接祖先节点的直接后代。就是说已经自动减少了一层。

 

      然而，某些在邻接表的设计中表现得很简单的查询，比如获取一个节点的直接父亲或者直接后代，在嵌套集设计中会变得比较复杂。在嵌套集中，如果需要查询一个节点的直接父亲，我们会这么做，比如要找到评论#6 的直接父亲：

SELECT parent.* FROM comments AS c JOIN comments AS parent ON c.nsleft BETWEEN parent.nsleft AND parent.nsrightLEFT OUTER JOIN comments AS in_between ON c.nsleft BETWEEN in_between.nsleft AND in_between.nsrightAND in_between.nsleft BETWEEN parent.nsleft AND parent.nsright WHERE c.comment_id = 6AND in_between.comment_id IS NULL;

总之有些复杂。

 

    对树进行操作，比如插入和移动节点，使用嵌套集会比其它设计复杂很多。当插入一个新节点时，你需要重新计算新插入节点的相邻兄弟节点、祖先节点和它祖先节点的兄弟，来确保他们的左右值都比这个新节点的左值大。同时，如果这个新节点时一个非叶子节点，你还要检查它的子孙节点。

 

    如果简单快速查询是整个程序中最重要的部分，嵌套集是最好的选择，比操作单独的节点要方便快捷很多。然而，嵌套集的插入和移动节点是比较复杂的，因为需要重新分配左右值，如果你的应用程序需要频繁的插入、删除节点，那么嵌套集可能并不合适。

 

 

三、闭包表

 

     闭包表是解决分级存储的一个简单而优雅的解决方案，它记录了树中所有节点间的关系，而不仅仅只有那些直接的父子节点。

 

     在设计评论系统时，我们额外创建了一个叫 tree_paths 表，它包含两列，每一列都指向 comments 中的外键。

 

     我们不再使用comments 表存储树的结构，而是将树中任何具有（祖先 一 后代）关系的节点对都存储在treepaths 表里，即使这两个节点之间不是直接的父子关系；同时，我们还增加一行指向节点自己。

 

祖先	后代	祖先	后代	祖先	后代	祖先	后代
1	1	1	7	4	6	7	7
1	2	2	2	4	7
1	3	2	3	5	5
1	4	3	3	5	6
1	5	4	4	5	7
1	6	4	5	6	6

      通过treepaths 表来获取祖先和后代比使用嵌套集更加的直接。例如要获取评论#4的后代，只需要在 treepaths 表中搜索祖先是评论 #4的行就行了。同样获取后代也是如此。

 

      要插入一个新的叶子节点，比如评论#6的一个子节点，应首先插入一条自己到自己的关系，然后搜索 treepaths 表中后代是评论#6 的节点，增加该节点和新插入节点的“祖先一后代”关系（新节点ID 应该为8）：

INSERT INTO treepaths (ancestor, descendant)SELECT t.ancestor, 8FROM treepaths AS tWHERE t.descendant = 6UNION ALL SELECT 8, 8;

 

要删除一个叶子节点，比如评论#7， 应删除所有treepaths 表中后代为评论 #7 的行：

DELETE FROM treepaths WHERE descendant = 7;

 

要删除一颗完整的子树，比如评论#4 和它所有的后代，可删除所有在 treepaths 表中后代为 #4的行，以及那些以评论#4后代为后代的行。

 

     闭包表的设计比嵌套集更加的直接，两者都能快捷地查询给定节点的祖先和后代，但是闭包表能更加简单地维护分层信息。这两个设计都比使用邻接表或者路径枚举更方便地查询给定节点的直接后代和祖先。

 

     然而你可以优化闭包表来使它更方便地查询直接父亲节点或者子节点： 在 treepaths 表中添加一个 path_length 字段。一个节点的自我引用的path_length 为0，到它直接子节点的path_length 为1，再下一层为2，以此类推。这样查询起来就方便多了。

 

总结：你该使用哪种设计：

     种设计都各有优劣，如何选择设计，依赖于应用程序的哪种操作是你最需要性能上的优化。

 

方案	表数量	查询子	查询树	插入	删除	引用完整性
邻接表	1	简单	困难	简单	简单	是
枚举路径	1	简单	简单	简单	简单	否
嵌套集	1	困难	简单	困难	困难	否
闭包表	2	简单	简单	简单	简单	是

层级数据设计比较

1、邻接表是最方便的设计，并且很多程序员都了解它

2、如果你使用的数据库支持WITH 或者 CONNECT BY PRIOR 的递归查询，那能使得邻接表的查询更高效。

3、枚举路径能够很直观地展示出祖先到后代之间的路径，但同时由于它不能确保引用完整性，使得这个设计非常脆弱。枚举路径也使得数据的存储变得比较冗余。

4、嵌套集是一个聪明的解决方案，但可能过于聪明，它不能确保引用完整性。最好在一个查询性能要求很高而对其他要求一般的场合来使用它。

5、闭包表是最通用的设计，并且以上的方案也只有它能允许一个节点属于多棵树。它要求一张额外的表来存储关系，使用空间换时间的方案减少操作过程中由冗余的计算所造成的消耗。

 

      这几种设计方案只是我们日常设计中的一部分，开发中肯定会遇到更多的选择方案。选择哪一种方案，是需要切合实际，根据自己项目的需求，结合方案的优劣，选择最适合的一种。

 

     我遇到一些开发人员，为了敷衍了事，在设计数据库表时，只考虑能否完成眼下的任务，不太注重以后拓展的问题，不考虑查询起来是否耗性能。可能前期数据量不多的时候，看不出什么影响，但数据量稍微多一点的话，就已经显而易见了（例如：可以使用外联接查询的，偏偏要使用子查询）。

 

     我觉得设计数据库是一个很有趣且充满挑战的工作，它有时能体现你的视野有多宽广，有时它能让你睡不着觉，总之痛并快乐着。

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!