Maison >développement back-end >Tutoriel Python >Introduction détaillée à l'algorithme KNN
Introduction détaillée à l'algorithme KNN
- PHP中文网original
- 2017-06-20 16:59:015152parcourir
Le nom complet de l'algorithme KNN est k-Nearest Neighbour, ce qui signifie K voisin le plus proche.
Description de l'algorithme
KNN est un algorithme de classification dont l'idée de base est de classer en mesurant la distance entre différentes valeurs de caractéristiques.
Le processus algorithmique est le suivant :
1. Préparez l'ensemble de données d'échantillon (chaque donnée de l'échantillon a été classée et possède une étiquette de classification
2. données pour la formation
3. Saisissez les données de test A
4. Calculez la distance entre A et chaque donnée dans l'ensemble d'échantillons
5. la distance de A Les k points les plus petits;
7. Calculer la fréquence d'apparition de la catégorie à laquelle appartiennent les k premiers points
8. classification prédite de A.
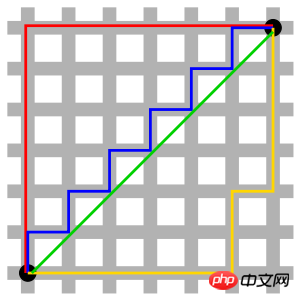

Quand p=1, c'est la distance de Manhattan
Quand p=2, c'est la distance euclidienne ; qui est la distance de Chebyshev.
5. Distance euclidienne standardisée
La distance euclidienne standardisée est un programme d'amélioration conçu pour remédier aux défauts de la distance euclidienne simple et peut être considérée comme une distance euclidienne pondérée.
L'idée dedistance euclidienne standard : étant donné que la distribution de chaque composante dimensionnelle des données est différente, "standardisez" d'abord chaque composante pour avoir une moyenne et une variance égales.
6. Distance Mahalanobis
représente la distance de covariance des données.
C'est une méthode efficace pour calculer la similarité de deux ensembles d'échantillons inconnus.
Dimensionnellement indépendant, ce qui peut éliminer l'interférence de corrélation entre les variables.
7. Distance Bhattacharyya En statistiques, la distance Bhattacharyya est utilisée pour mesurer deux distributions de probabilité discrètes. Il est souvent utilisé en classification pour mesurer la séparabilité entre les classes.
8. Distance de Hamming (distance de Hamming)
La distance de Hamming entre deux cordes de longueur égale s1 et s2 est définie comme la quantité minimale de travail requise pour changer l'une dans l'autre. Nombre de remplacements.
Par exemple, la distance de Hamming entre les chaînes "1111" et "1001" est de 2.
Application :
Codage des informations (afin d'améliorer la tolérance aux pannes, la distance minimale de Hamming entre les codes doit être aussi grande que possible).
9. Cosinus de l'angle inclus (Cosinus)
En géométrie, le cosinus de l'angle inclus peut être utilisé pour mesurer la différence de direction de deux vecteurs, et en data mining, il peut être utilisé pour mesurer la différence entre les vecteurs d’échantillon.
10. Coefficient de similarité de Jaccard (coefficient de similarité de Jaccard)
La distance de Jaccard mesure la distinction entre deux ensembles en utilisant la proportion d'éléments différents dans tous les éléments des deux ensembles.
Le coefficient de similarité Jaccard peut être utilisé pour mesurer la similarité des échantillons.
11. Coefficient de corrélation de Pearson
Le coefficient de corrélation de Pearson, également appelé coefficient de corrélation produit-moment de Pearson, est un coefficient de corrélation linéaire. Le coefficient de corrélation de Pearson est une statistique utilisée pour refléter le degré de corrélation linéaire entre deux variables.
L'impact des grandes dimensions sur la mesure de la distance :
Lorsqu'il y a plus de variables, la capacité discriminante de la distance euclidienne s'aggrave.
L'impact de la plage variable sur la distance :
Les variables avec des plages de valeurs plus grandes jouent souvent un rôle dominant dans les calculs de distance, les variables doivent donc être standardisées en premier.
La taille de k
k est trop petite, les résultats de classification sont facilement affectés par les points de bruit, et l'erreur augmentera
k est trop grande, et les voisins les plus proches peuvent ; inclure trop d'autres points de catégories (pondérer la distance peut réduire l'impact du réglage de la valeur k
k=N (nombre d'échantillons) n'est absolument pas souhaitable, car quelle que soit l'instance d'entrée à ce moment-là, elle l'est tout simplement ; prédit qu'il appartient à la classe de formation avec le plus d'instances, le modèle est trop simple et ignore beaucoup d'informations utiles dans les instances de formation.
Dans les applications pratiques, la valeur K prend généralement une valeur relativement petite. Par exemple, la méthode de validation croisée est utilisée (en termes simples, certains échantillons sont utilisés comme ensemble d'entraînement et d'autres comme test. set) pour sélectionner la valeur K optimale.
Règle générale : k est généralement inférieur à la racine carrée du nombre d'échantillons d'apprentissage.
Avantages et inconvénients
1. Avantages
Simple, facile à comprendre, facile à mettre en œuvre, haute précision et non sensible aux valeurs aberrantes.
2. Inconvénients
KNN est un algorithme paresseux à construire un modèle, mais la surcharge système liée à la classification des données de test est importante (grande quantité de calculs et surcharge de mémoire importante). , car il doit analyser tous les échantillons d'entraînement et calculer la distance.
Portée applicable
Type numérique et type nominal (ayant un nombre fini de valeurs différentes, et les valeurs sont désordonnées).
Par exemple, prévision du taux de désabonnement des clients, détection des fraudes, etc.
Implémentation de l'algorithme
Nous prenons ici python comme exemple pour décrire l'implémentation de l'algorithme KNN basé sur la distance euclidienne.
Formule de distance euclidienne :

Exemple de code prenant la distance euclidienne comme exemple :
#! /usr/bin/env python#-*- coding:utf-8 -*-# E-Mail : Mike_Zhang@live.comimport mathclass KNN: def __init__(self,trainData,trainLabel,k):
self.trainData = trainData
self.trainLabel = trainLabel
self.k = k def predict(self,inputPoint):
retLable = "None"arr=[]for vector,lable in zip(self.trainData,self.trainLabel):
s = 0for i,n in enumerate(vector) :
s += (n-inputPoint[i]) ** 2arr.append([math.sqrt(s),lable])
arr = sorted(arr,key=lambda x:x[0])[:self.k]
dtmp = {}for k,v in arr :if not v in dtmp : dtmp[v]=0
dtmp[v] += 1retLable,_ = sorted(dtmp.items(),key=lambda x:x[1],reverse=True)[0] return retLable
data = [
[1.0, 1.1],
[1.0, 1.0],
[0.0, 0.0],
[0.0, 0.1],
[1.3, 1.1],
]
labels = ['A','A','B','B','A']
knn = KNN(data,labels,3)print knn.predict([1.2, 1.1])
print knn.predict([0.2, 0.1])Le L'implémentation ci-dessus est relativement simple. Vous pouvez utiliser des bibliothèques prêtes à l'emploi en développement, telles que scikit-learn :
Algorithm Application
- Reconnaître les chiffres manuscrits
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

