Comment gérer les matrices clairsemées ? Implémentation Python du didacticiel de matrice clairsemée

Cet article présente principalement l'exemple de code pour implémenter une matrice clairsemée en python. L'éditeur pense que c'est plutôt bon. Maintenant, je vais le partager avec vous et le donner comme référence. Suivons l'éditeur et jetons un coup d'œil

Dans la pratique de l'ingénierie, dans la plupart des cas, les grandes matrices sont généralement des matrices clairsemées, donc comment gérer les matrices clairsemées est très important dans la pratique. Cet article prend l'implémentation en Python comme exemple. Tout d'abord, explorons comment les matrices clairsemées sont stockées et représentées.

1. Une étude préliminaire sur le module sparse

Dans le module scipy en python, il existe un module appelé module sparse, qui est spécifiquement conçu pour résoudre des problèmes clairsemés. matrices. La majeure partie du contenu de cet article est en fait basée sur le module sparse.

La première étape est d'importer le module sparse

>>> from scipy import sparse

puis d'aider, jetons un coup d'oeil d'abord

>>> help(sparse)

Trouver directement ce que nous sommes le plus préoccupé par la partie :

  Usage information
  =================

  There are seven available sparse matrix types:

    1. csc_matrix: Compressed Sparse Column format
    2. csr_matrix: Compressed Sparse Row format
    3. bsr_matrix: Block Sparse Row format
    4. lil_matrix: List of Lists format
    5. dok_matrix: Dictionary of Keys format
    6. coo_matrix: COOrdinate format (aka IJV, triplet format)
    7. dia_matrix: DIAgonal format

  To construct a matrix efficiently, use either dok_matrix or lil_matrix.
  The lil_matrix class supports basic slicing and fancy
  indexing with a similar syntax to NumPy arrays. As illustrated below,
  the COO format may also be used to efficiently construct matrices.

  To perform manipulations such as multiplication or inversion, first
  convert the matrix to either CSC or CSR format. The lil_matrix format is
  row-based, so conversion to CSR is efficient, whereas conversion to CSC
  is less so.

  All conversions among the CSR, CSC, and COO formats are efficient,
  linear-time operations.

Grâce à cette description, nous avons une compréhension générale du module sparse. Il existe 7 façons de stocker des matrices clairsemées dans le module clairsemé. Ensuite, nous présenterons ces 7 méthodes une par une.

2.coo_matrix

coo_matrix est la méthode de stockage la plus simple. Utilisez trois tableaux row, col et data pour stocker les informations des éléments non nuls. Les trois tableaux ont la même longueur, row contient la ligne d'éléments, col contient la colonne d'éléments et data contient la valeur de l'élément. De manière générale, coo_matrix est principalement utilisé pour créer des matrices, car coo_matrix ne peut pas ajouter, supprimer ou modifier des éléments de la matrice. Une fois la matrice créée avec succès, elle sera convertie en d'autres formes de matrices.

>>> row = [2,2,3,2]
>>> col = [3,4,2,3]
>>> c = sparse.coo_matrix((data,(row,col)),shape=(5,6))
>>> print c.toarray()
[[0 0 0 0 0 0]
 [0 0 0 0 0 0]
 [0 0 0 5 2 0]
 [0 0 3 0 0 0]
 [0 0 0 0 0 0]]

Une chose à noter est que lorsque vous utilisez coo_matrix pour créer une matrice, les mêmes coordonnées de ligne et de colonne peuvent apparaître plusieurs fois. Une fois la matrice réellement créée, les valeurs de coordonnées correspondantes seront additionnées pour obtenir le résultat final.

3.dok_matrix et lil_matrix

Le scénario applicable pour dok_matrix et lil_matrix consiste à ajouter progressivement des éléments de la matrice. La stratégie de doc_matrix consiste à utiliser un dictionnaire pour enregistrer les éléments de la matrice qui ne valent pas 0. Naturellement, la clé du dictionnaire stocke l'ancêtre des informations de position de l'élément enregistré, et la valeur est la valeur spécifique de l'élément enregistré.

>>> import numpy as np
>>> from scipy.sparse import dok_matrix
>>> S = dok_matrix((5, 5), dtype=np.float32)
>>> for i in range(5):
...   for j in range(5):
...       S[i, j] = i + j
...
>>> print S.toarray()
[[ 0. 1. 2. 3. 4.]
 [ 1. 2. 3. 4. 5.]
 [ 2. 3. 4. 5. 6.]
 [ 3. 4. 5. 6. 7.]
 [ 4. 5. 6. 7. 8.]]

lil_matrix utilise deux listes pour stocker des éléments non nuls. data stocke les éléments non nuls dans chaque ligne et rows stocke les colonnes dans lesquelles se trouvent les éléments non nuls. Ce format est également idéal pour ajouter des éléments un par un et récupérer rapidement les données liées aux lignes.

>>> from scipy.sparse import lil_matrix
>>> l = lil_matrix((6,5))
>>> l[2,3] = 1
>>> l[3,4] = 2
>>> l[3,2] = 3
>>> print l.toarray()
[[ 0. 0. 0. 0. 0.]
 [ 0. 0. 0. 0. 0.]
 [ 0. 0. 0. 1. 0.]
 [ 0. 0. 3. 0. 2.]
 [ 0. 0. 0. 0. 0.]
 [ 0. 0. 0. 0. 0.]]
>>> print l.data
[[] [] [1.0] [3.0, 2.0] [] []]
>>> print l.rows
[[] [] [3] [2, 4] [] []]

Il ressort facilement de l'analyse ci-dessus que les deux méthodes ci-dessus de construction de matrices clairsemées sont généralement utilisées pour construire des matrices en ajoutant progressivement des éléments non nuls, puis en les convertissant en d'autres méthodes qui peuvent être rapide La méthode de stockage matricielle calculée.

4.dia_matrix

Il s'agit d'une méthode de stockage en diagonale. Où les colonnes représentent les diagonales et les lignes représentent les lignes. Si les éléments de la diagonale sont tous à 0, ils sont omis.

Si la matrice d'origine est une matrice diagonale, le taux de compression sera très élevé.

Si vous trouvez une photo sur Internet, vous comprendrez facilement le principe.

5.csr_matrix et csc_matrix

csr_matrix, le nom complet est Compressed Sparse Row, est un système basé sur des lignes traitement des matrices compressées. La RSE nécessite trois types de données : les valeurs numériques, les numéros de colonnes et les décalages de lignes. CSR est une méthode de codage dans laquelle les significations des valeurs numériques et des numéros de colonnes sont cohérentes avec celles de coo. Le décalage de ligne indique la position de décalage de départ du premier élément d'une ligne dans les valeurs.

J'ai aussi trouvé une photo sur Internet qui reflète mieux le principe.

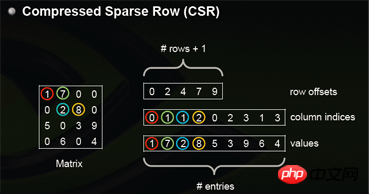
Voyons comment l'utiliser en python : Et

>>> from scipy.sparse import csr_matrix
>>> indptr = np.array([0, 2, 3, 6])
>>> indices = np.array([0, 2, 2, 0, 1, 2])
>>> data = np.array([1, 2, 3, 4, 5, 6])
>>> csr_matrix((data, indices, indptr), shape=(3, 3)).toarray()
array([[1, 0, 2],
    [0, 0, 3],
    [4, 5, 6]])

, n'est-ce pas difficile à comprendre ?

Regardons ce que dit le document

 Notes
 | -----
 |
 | Sparse matrices can be used in arithmetic operations: they support
 | addition, subtraction, multiplication, pision, and matrix power.
 |
 | Advantages of the CSR format
 |  - efficient arithmetic operations CSR + CSR, CSR * CSR, etc.
 |  - efficient row slicing
 |  - fast matrix vector products
 |
 | Disadvantages of the CSR format
 |  - slow column slicing operations (consider CSC)
 |  - changes to the sparsity structure are expensive (consider LIL or DOK)

Il n'est pas difficile de voir que csr_matrix est plus adapté aux opérations matricielles réelles.

Quant à csc_matrix, il est similaire à csr_matrix, mais il est compressé en fonction des colonnes et ne sera pas présenté séparément.

6.bsr_matrix

Le format Block Sparse Row, comme son nom l'indique, compresse la matrice en fonction de l'idée de blocage.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!