Explication détaillée de la façon d'implémenter des arbres binaires et sept méthodes de traversée dans la programmation Python

Cet article présente principalement PythonProgrammation pour implémenter des arbres binaires et sept méthodes de traversée. Il analyse également en détail la définition des arbres binaires Python et les techniques d'opération de traversée courantes sous la forme de. exemples.Amis dans le besoin Vous pouvez vous référer à ce qui suit

Cet article décrit l'implémentation des arbres binaires et des méthodes de traversée en Python. Partagez-le avec tout le monde pour votre référence, les détails sont les suivants :

Introduction :

L'arbre est un type de structure de données très important, son objectif principal Il est utilisé pour améliorer l'efficacité de la recherche et est plus efficace lorsque des recherches répétées sont nécessaires, comme les arbres de tri binaire et les arbres FP. De plus, il peut être utilisé pour améliorer l’efficacité du codage, comme l’arbre de Huffman.

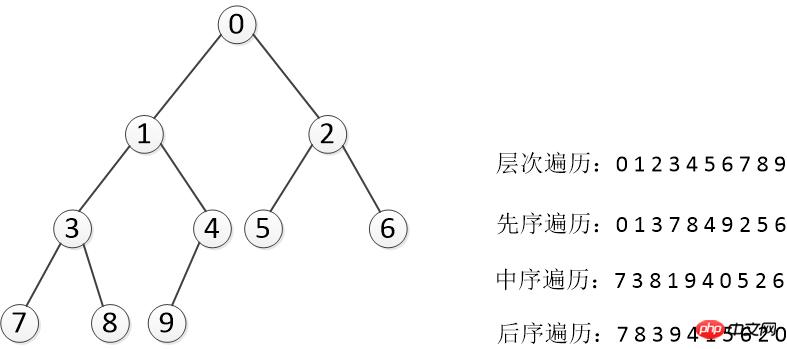
Code :

Utilisez Python pour implémenter la construction d'arbres et plusieurs algorithmes de traversée, bien que ce ne soit pas le cas difficile, mais j'ai quand même organisé et résumé le code. Fonctions d'implémentation :

① Construction d'arbre
② Récursion Implémenter le parcours de pré-commande, le parcours dans l'ordre, le parcours de post-commande
③ Stack implémente le parcours de pré-commande, dans -order traversal, Post-order traversal
④ Queue implémente le parcours hiérarchique

#coding=utf-8
class Node(object):
  """节点类"""
  def init(self, elem=-1, lchild=None, rchild=None):
    self.elem = elem
    self.lchild = lchild
    self.rchild = rchild
class Tree(object):
  """树类"""
  def init(self):
    self.root = Node()
    self.myQueue = []
  def add(self, elem):
    """为树添加节点"""
    node = Node(elem)
    if self.root.elem == -1: # 如果树是空的，则对根节点赋值
      self.root = node
      self.myQueue.append(self.root)
    else:
      treeNode = self.myQueue[0] # 此结点的子树还没有齐。
      if treeNode.lchild == None:
        treeNode.lchild = node
        self.myQueue.append(treeNode.lchild)
      else:
        treeNode.rchild = node
        self.myQueue.append(treeNode.rchild)
        self.myQueue.pop(0) # 如果该结点存在右子树，将此结点丢弃。
  def front_digui(self, root):
    """利用递归实现树的先序遍历"""
    if root == None:
      return
    print root.elem,
    self.front_digui(root.lchild)
    self.front_digui(root.rchild)
  def middle_digui(self, root):
    """利用递归实现树的中序遍历"""
    if root == None:
      return
    self.middle_digui(root.lchild)
    print root.elem,
    self.middle_digui(root.rchild)
  def later_digui(self, root):
    """利用递归实现树的后序遍历"""
    if root == None:
      return
    self.later_digui(root.lchild)
    self.later_digui(root.rchild)
    print root.elem,
  def front_stack(self, root):
    """利用堆栈实现树的先序遍历"""
    if root == None:
      return
    myStack = []
    node = root
    while node or myStack:
      while node:           #从根节点开始，一直找它的左子树
        print node.elem,
        myStack.append(node)
        node = node.lchild
      node = myStack.pop()      #while结束表示当前节点node为空，即前一个节点没有左子树了
      node = node.rchild         #开始查看它的右子树
  def middle_stack(self, root):
    """利用堆栈实现树的中序遍历"""
    if root == None:
      return
    myStack = []
    node = root
    while node or myStack:
      while node:           #从根节点开始，一直找它的左子树
        myStack.append(node)
        node = node.lchild
      node = myStack.pop()      #while结束表示当前节点node为空，即前一个节点没有左子树了
      print node.elem,
      node = node.rchild         #开始查看它的右子树
  def later_stack(self, root):
    """利用堆栈实现树的后序遍历"""
    if root == None:
      return
    myStack1 = []
    myStack2 = []
    node = root
    myStack1.append(node)
    while myStack1:          #这个while循环的功能是找出后序遍历的逆序，存在myStack2里面
      node = myStack1.pop()
      if node.lchild:
        myStack1.append(node.lchild)
      if node.rchild:
        myStack1.append(node.rchild)
      myStack2.append(node)
    while myStack2:             #将myStack2中的元素出栈，即为后序遍历次序
      print myStack2.pop().elem,
  def level_queue(self, root):
    """利用队列实现树的层次遍历"""
    if root == None:
      return
    myQueue = []
    node = root
    myQueue.append(node)
    while myQueue:
      node = myQueue.pop(0)
      print node.elem,
      if node.lchild != None:
        myQueue.append(node.lchild)
      if node.rchild != None:
        myQueue.append(node.rchild)
if name == 'main':
  """主函数"""
  elems = range(10)      #生成十个数据作为树节点
  tree = Tree()     #新建一个树对象
  for elem in elems:
    tree.add(elem)      #逐个添加树的节点
  print '队列实现层次遍历:'
  tree.level_queue(tree.root)
  print '\n\n递归实现先序遍历:'
  tree.front_digui(tree.root)
  print '\n递归实现中序遍历:'
  tree.middle_digui(tree.root)
  print '\n递归实现后序遍历:'
  tree.later_digui(tree.root)
  print '\n\n堆栈实现先序遍历:'
  tree.front_stack(tree.root)
  print '\n堆栈实现中序遍历:'
  tree.middle_stack(tree.root)
  print '\n堆栈实现后序遍历:'
  tree.later_stack(tree.root)

Résumé :

Le parcours principal de l'arbre Il existe deux types, l'un est le parcours en profondeur d'abord, comme le pré-ordre, l'ordre intermédiaire et le post-ordre ; l'autre est le parcours en largeur d'abord, comme le parcours hiérarchique. La différence entre les deux n'est pas très évidente dans la structure arborescente, mais lorsqu'on s'étend d'un arbre à un graphe orienté en passant par un graphe non orienté, l'efficacité et l'effet de la recherche en profondeur et de la recherche en largeur d'abord sont toujours très génial.

La profondeur d'abord utilise généralement la récursivité, et la largeur d'abord utilise généralement des files d'attente. En général, la plupart des algorithmes pouvant être implémentés par récursion peuvent également être implémentés à l’aide de piles.

J'ai l'impression qu'il existe un moyen de construire un arbre de manière récursive, mais je n'ai jamais réussi à comprendre comment le construire. Après y avoir réfléchi attentivement, j'ai réalisé que la pensée récursive est quelque peu similaire à l'algorithme axé sur la profondeur d'abord, et que la construction de l'arbre doit être axée sur la largeur. Si la récursivité est utilisée, il doit y avoir une condition de terminaison, telle que spécifier la profondeur de l'arborescence, etc. Sinon, l’arbre construit sera biaisé vers le sous-arbre unique de gauche ou vers le sous-arbre unique de droite. Par conséquent, il est préférable d’utiliser des files d’attente pour la construction générale d’arborescences.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!