Explication détaillée d'exemples d'implémentation du tri Hill en Python

Cet article présente principalement l'implémentation du tri Hill en Python. Le tri Hill programmé a une certaine valeur de référence. Les amis intéressés peuvent s'y référer

Observez le "tri par insertion" : En fait, ce n'est pas difficile à faire. constater qu'elle a un défaut :

Si les données sont "5, 4, 3, 2, 1", à ce moment nous insérerons les enregistrements du "bloc non ordonné" dans la "Séquence" avec block", on estime que nous allons planter, et la position sera déplacée à chaque insertion. À ce stade, l'efficacité du tri par insertion peut être imaginée.

Le shell a amélioré l'algorithme basé sur cette faiblesse et incorporé une idée appelée "réduction de la méthode de tri incrémental". C'est en fait assez simple, mais quelque chose à noter est :

incrément Ce n'est pas aléatoire. , mais il y a des règles à suivre.

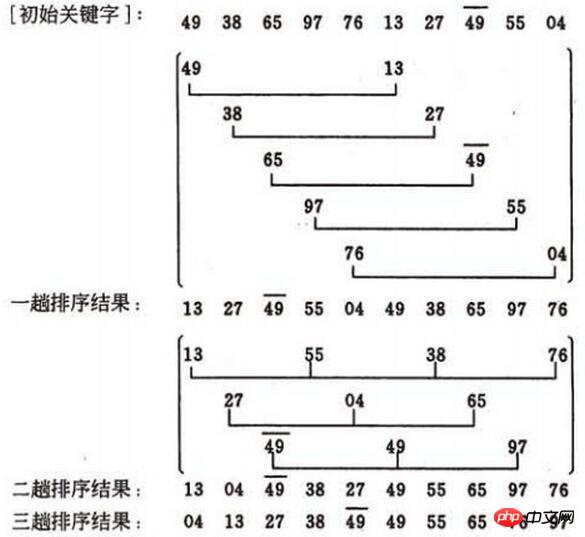
L'analyse de la rapidité du tri Hill est difficile Le nombre de comparaisons de codes clés et le nombre de déplacements d'enregistrements dépendent de la sélection de la séquence de facteurs d'incrémentation d, dans certaines circonstances, ce qui suit peut estimer avec précision le nombre de comparaisons de codes clés et le nombre de mouvements enregistrés. Personne n'a encore donné de méthode pour sélectionner la meilleure séquence de facteurs incrémentaux. La séquence de facteurs incrémentaux peut être prise de différentes manières, y compris les nombres impairs et les nombres premiers. Cependant, il convient de noter qu'il n'y a pas de facteurs communs entre les facteurs incrémentaux sauf 1, et que le dernier facteur incrémentiel doit être 1. La méthode de tri Hill est une méthode de tri instable. Tout d'abord, nous devons clarifier la méthode d'incrémentation (les images ici sont copiées à partir de blogs d'autres personnes, l'incrément est un nombre impair, et ma programmation ci-dessous utilise un nombre pair) :

Le premier incrément La méthode de sélection est : d=count/2;

Le deuxième incrément est : d=(count/2)/2;

Finalement, on passe à : d =1;

D'accord, faites attention à l'image. L'incrément d1=5 dans le premier passage divise les 10 enregistrements à trier en 5 sous-séquences

Effectuez respectivement un tri par insertion directe. le résultat est (13, 27, 49, 55, 04, 49, 38, 65, 97, 76)

Le deuxième incrément de passe d2=3, divise les 10 enregistrements à mettre en file d'attente en 3 sous-séquences, et effectuez respectivement une insertion directe, le résultat est (13, 04, 49, 38, 27, 49, 55, 65, 97, 76)L'incrément d3=1 du troisième passage, insertion directe. le tri est effectué sur toute la séquence,

Le résultat final

est (04, 13, 27, 38, 49, 49, 55, 65, 76, 97)Voici le point clé. Lorsque l'incrément diminue jusqu'à 1, la séquence est fondamentalement dans l'ordre La dernière passe du tri Hill est un tri par insertion directe, ce qui est proche de la meilleure situation. Les ajustements « macro » dans les passes précédentes peuvent être considérés comme le prétraitement de la dernière passe, ce qui est plus efficace que d'effectuer un seul tri par insertion directe.

J'apprends python et aujourd'hui j'ai utilisé python pour implémenter le tri Hill.

Sortie :

> : [49, 38, 65, 97, 76, 13, 27, 49, 55, 4]

def ShellInsetSort(array, len_array, dk): # 直接插入排序
 for i in range(dk, len_array): # 从下标为dk的数进行插入排序
 position = i
 current_val = array[position] # 要插入的数
 index = i
 j = int(index / dk) # index与dk的商
 index = index - j * dk

 # while True: # 找到第一个的下标，在增量为dk中，第一个的下标index必然 0<=index<dk
 # index = index - dk
 # if 0<=index and index <dk:
 # break

 # position>index,要插入的数的下标必须得大于第一个下标
 while position > index and current_val < array[position-dk]:
 array[position] = array[position-dk] # 往后移动
 position = position-dk
 else:
 array[position] = current_val


def ShellSort(array, len_array): # 希尔排序
 dk = int(len_array/2) # 增量
 while(dk >= 1):
 ShellInsetSort(array, len_array, dk)
 print(">>:",array)
 dk = int(dk/2)

if __name__ == "__main__":
 array = [49, 38, 65, 97, 76, 13, 27, 49, 55, 4]
 print(">:", array)
 ShellSort(array, len(array))

>> : [13, 27, 49, 55, 4, 49, 38, 65, 97, 76]

>> : [4, 27, 13, 49, 38, 55, 49, 65, 97, 76]

>> : [4, 13, 27, 38, 49, 49, 55, 65, 76, 97]

Vous devez d'abord Si vous savez faire du tri par insertion, si vous ne savez pas comment le faire, vous ne pourrez certainement pas le comprendre.

Le tri par insertion consiste à insérer et trier les nombres dans les trois cases jaunes de l'image ci-dessus. Par exemple : 13, 55, 38, 76

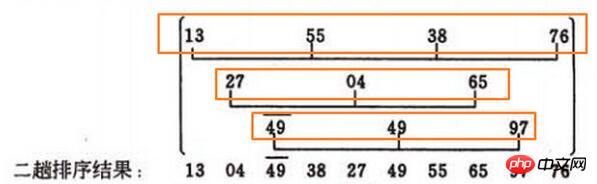Regardez directement 55, 55<13, sans bouger. Regardez ensuite 38, 38<55, puis 55 est reculé et les données deviennent [13, 55, 55, 76]. Comparez ensuite 13<38, puis 38 remplace 55 et devient [13, 38, 55, 76] . Le reste est le même, omis.

Il y a un problème ici, par exemple, la deuxième case jaune

[27, 4, 65], 4<27, puis 27 recule, puis 4 remplace la première, et la donnée devient [ 4, 27, 65],

Mais comment l'ordinateur sait-il que 4 est le premier ??

Mon approche consiste à d'abord trouver le premier de [27, 4, 65] ] L'indice d'un nombre. Dans cet exemple, l'indice de 27 est 1. Lorsque l'indice du nombre à insérer est supérieur au premier indice 1, il peut être déplacé vers l'arrière

Le numéro précédent ne peut pas être déplacé vers l'arrière , l'une est. S'il y a des données devant et qu'elles sont inférieures au nombre à insérer, vous ne pouvez les insérer qu'après. Un autre, très important, lorsque le nombre à insérer est plus petit que tous les nombres précédents, le nombre à insérer doit être placé en premier. A ce moment, l'indice du nombre à insérer = l'indice du premier nombre. (Ce passage n'est peut-être pas très compréhensible pour les débutants...) Afin de retrouver l'indice du premier nombre, la première chose à laquelle j'ai pensé a été d'utiliser une boucle, jusqu'au début :

Lors du débogage, j'ai trouvé que l'utilisation de boucles est une perte de temps, surtout lorsque l'incrément d=1 afin d'insérer le dernier numéro. dans la liste directement, il faut boucler et soustraire. 1. Jusqu'à l'indice du premier nombre. Plus tard, j'ai appris intelligemment et j'ai utilisé la méthode suivante :

while True: # 找到第一个的下标，在增量为dk中，第一个的下标index必然 0<=index<dk
 index = index - dk
 if 0<=index and index <dk:
 break

. Complexité temporelle :

La complexité temporelle du tri Hill est fonction de la séquence d'incréments prise, et elle est difficile à analyser avec précision. Certaines publications soulignent que lorsque la séquence incrémentielle est d[k]=2^(t-k+1), la complexité temporelle du tri Hill est O(n^1.5), où t est le tri Nombre de voyages.

Stabilité : Instable

Effet de tri des collines :

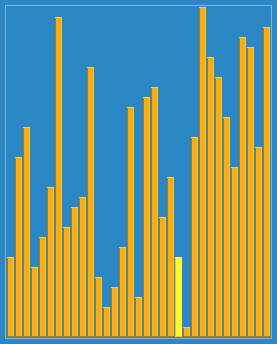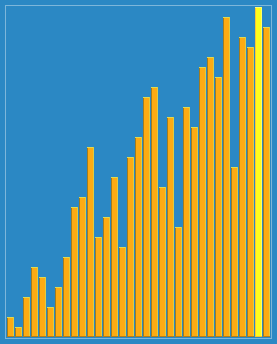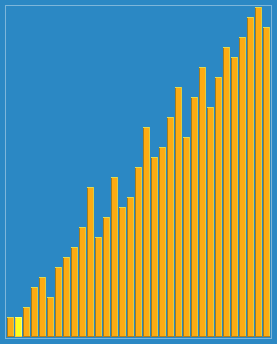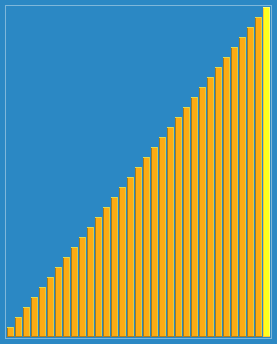
Référence : La programmation est mise en œuvre par moi-même. Il est recommandé de déboguer et d'examiner le processus en cours

Huit algorithmes de tri majeurs en C++

Expérimentez visuellement et intuitivement plusieurs algorithmes de tri couramment utilisés

Sept série d'algorithmes de tri classiques en C# (Partie 2)

1 L'apprentissage non systématique est également une perte de temps 2. Soyez une personne technique qui peut apprécier la beauté, comprendre l'art et être bonne en art

.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!