Maison >développement back-end >Tutoriel Python >Explication détaillée de l'utilisation de la méthode des moindres carrés en Python
Explication détaillée de l'utilisation de la méthode des moindres carrés en Python
- 高洛峰original
- 2017-03-27 15:15:5311356parcourir
La raison pour laquelle je dis « utiliser » plutôt que « implémenter » est que les bibliothèques de classes associées à Python nous ont déjà aidé à implémenter des algorithmes spécifiques, et nous avons seulement besoin d'apprendre à les utiliser. Avec la maîtrise et l'accumulation progressives de la technologie, lorsque les algorithmes de la bibliothèque de classes ne peuvent plus répondre à nos propres besoins, nous pouvons également essayer d'implémenter divers algorithmes à notre manière.
Revenons au sujet, qu'est-ce que la « méthode des moindres carrés » ?
Définition : La méthode des moindres carrés (également connue sous le nom de méthode des moindres carrés) est une technique d'optimisation mathématique qui trouve la meilleure correspondance de fonction des données en minimisant la somme des carrés des erreurs.
Fonction : La méthode des moindres carrés peut être utilisée pour obtenir facilement des données inconnues et minimiser la somme des erreurs carrées entre les données obtenues et les données réelles.
Principe : Déterminer la position de la droite avec la "somme minimale des carrés des résidus" (en statistique mathématique, le résidu fait référence à la différence entre la valeur réelle observée et la valeur estimée)
Idée de base : pour le modèle de régression linéaire univariée, en supposant que n ensembles de valeurs d'observation (X1, Y1), (X2, Y2), ..., (Xn, Yn) sont obtenus à partir de la population. points dans le plan, d'innombrables courbes peuvent être utilisées pour l'ajustement. La régression linéaire nécessite que la fonction de régression de l'échantillon s'adapte au mieux à cet ensemble de valeurs. En d'autres termes, cette ligne droite doit être aussi centrée que possible dans les données de l'échantillon. Par conséquent, le critère de sélection de la meilleure courbe d'ajustement peut être déterminé comme suit : minimiser l'erreur d'ajustement totale (c'est-à-dire l'erreur résiduelle totale).
Le code d'implémentation est le suivant, et le code a été commenté en détail :
##最小二乘法
import numpy as np ##科学计算库
import scipy as sp ##在numpy基础上实现的部分算法库
import matplotlib.pyplot as plt ##绘图库
from scipy.optimize import leastsq ##引入最小二乘法算法
'''
设置样本数据,真实数据需要在这里处理
'''
##样本数据(Xi,Yi),需要转换成数组(列表)形式
Xi=np.array([6.19,2.51,7.29,7.01,5.7,2.66,3.98,2.5,9.1,4.2])
Yi=np.array([5.25,2.83,6.41,6.71,5.1,4.23,5.05,1.98,10.5,6.3])
'''
设定拟合函数和偏差函数
函数的形状确定过程:
1.先画样本图像
2.根据样本图像大致形状确定函数形式(直线、抛物线、正弦余弦等)
'''
##需要拟合的函数func :指定函数的形状
def func(p,x):
k,b=p
return k*x+b
##偏差函数:x,y都是列表:这里的x,y更上面的Xi,Yi中是一一对应的
def error(p,x,y):
return func(p,x)-y
'''
主要部分:附带部分说明
1.leastsq函数的返回值tuple,第一个元素是求解结果,第二个是求解的代价值(个人理解)
2.官网的原话(第二个值):Value of the cost function at the solution
3.实例:Para=>(array([ 0.61349535, 1.79409255]), 3)
4.返回值元组中第一个值的数量跟需要求解的参数的数量一致
'''
#k,b的初始值,可以任意设定,经过几次试验,发现p0的值会影响cost的值:Para[1]
p0=[1,20]
#把error函数中除了p0以外的参数打包到args中(使用要求)
Para=leastsq(error,p0,args=(Xi,Yi))
#读取结果
k,b=Para[0]
print("k=",k,"b=",b)
print("cost:"+str(Para[1]))
print("求解的拟合直线为:")
print("y="+str(round(k,2))+"x+"+str(round(b,2)))
'''
绘图,看拟合效果.
matplotlib默认不支持中文,label设置中文的话需要另行设置
如果报错,改成英文就可以
'''
#画样本点
plt.figure(figsize=(8,6)) ##指定图像比例: 8:6
plt.scatter(Xi,Yi,color="green",label="样本数据",linewidth=2)
#画拟合直线
x=np.linspace(0,12,100) ##在0-15直接画100个连续点
y=k*x+b ##函数式
plt.plot(x,y,color="red",label="拟合直线",linewidth=2)
plt.legend() #绘制图例
plt.show()Le résultat est le suivant :
Résultat de sortie :
k= 0.900458420439 b= 0.831055638877
coût : 1
La droite ajustée est :
y=0.9x+0.83
Résultat du dessin :
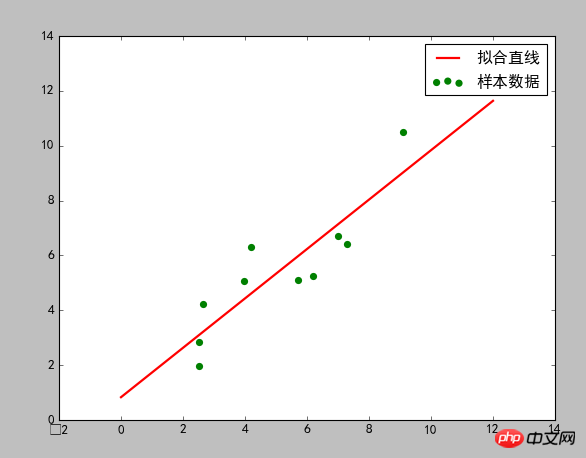
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

