Maison >Java >javaDidacticiel >Analyse approfondie de l'implémentation Java des arbres rouge-noir (photo)
Analyse approfondie de l'implémentation Java des arbres rouge-noir (photo)
- 黄舟original
- 2017-03-20 10:37:361751parcourir
L'arbre rouge-noir est un type d'arbre de recherche binaire équilibré. Afin de comprendre en profondeur les arbres rouge-noir, nous devons commencer par des arbres de recherche binaires.
Analyse approfondie de limplémentation Java des arbres rouge-noir (photo)
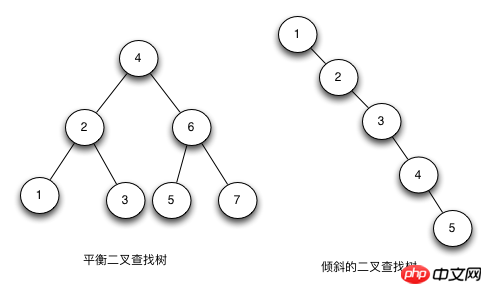
Binary Search Tree (Analyse approfondie de limplémentation Java des arbres rouge-noir (photo) en abrégé) est un arbre binaire. La valeur de son nœud enfant gauche est inférieure à la valeur du nœud parent et à la valeur du nœud droit. est plus grand que la valeur du nœud parent. Sa hauteur détermine son efficacité de recherche.
Dans des circonstances idéales, la complexité temporelle de l'ajout, de la suppression et de la modification d'un arbre de recherche binaire est O(logN) (où N est le nombre de nœuds), et dans le pire des cas, elle est O(N) . On dit qu’un arbre de recherche binaire est équilibré lorsque sa hauteur est logN 1.
Opération de recherche Analyse approfondie de limplémentation Java des arbres rouge-noir (photo)
T key = a search key
Node root = point to the root of a Analyse approfondie de limplémentation Java des arbres rouge-noir (photo)
while(true){
if(root==null){
break;
}
if(root.value.equals(key)){
return root;
}
else if(key.compareTo(root.value)<0){
root = root.left;
}
else{
root = root.right;
}
}
return null;Comme le montre le programme, lorsque Analyse approfondie de limplémentation Java des arbres rouge-noir (photo) recherche, il compare d'abord avec le nœud actuel :
Si égal, renvoie le nœud actuel
S'il est inférieur au nœud actuel, continuez à rechercher le nœud gauche du nœud actuel ;
S'il est supérieur au nœud actuel, continuez à rechercher le nœud droit du nœud actuel.
Jusqu'à ce que le pointeur de nœud actuel soit vide ou que le nœud correspondant soit trouvé, la recherche du programme se termine.
Opération d'insertion de Analyse approfondie de limplémentation Java des arbres rouge-noir (photo)
Node node = create a new node with specify value
Node root = point the root node of a Analyse approfondie de limplémentation Java des arbres rouge-noir (photo)
Node parent = null;
//find the parent node to append the new node
while(true){
if(root==null)break;
parent = root;
if(node.value.compareTo(root.value)<=0){
root = root.left;
}else{
root = root.right;
}
}
if(parent!=null){
if(node.value.compareTo(parent.value)<=0){//append to left
parent.left = node;
}else{//append to right
parent.right = node;
}
}L'opération d'insertion trouve d'abord le nœud parent du nœud à insérer via une boucle. La logique de recherche du nœud parent est la même. plus petit que la taille à gauche, un grand à droite. Après avoir trouvé le nœud parent, comparez le nœud parent, le plus petit est inséré dans le nœud gauche du nœud parent et le plus grand est inséré dans le nœud droit du nœud parent.
Opération de suppression de Analyse approfondie de limplémentation Java des arbres rouge-noir (photo)
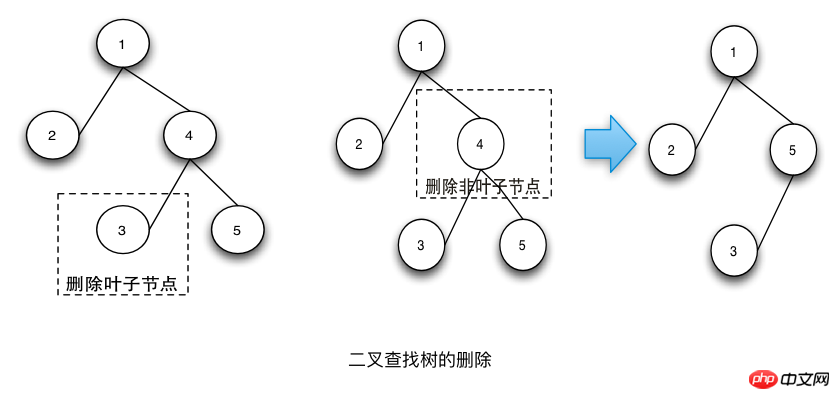
Les étapes de l'opération de suppression sont les suivantes :
Trouver le nœud à supprimer.
Si le nœud à supprimer est un nœud feuille, supprimez-le directement.
Si le nœud à supprimer n'est pas un nœud feuille, recherchez d'abord le nœud successeur du parcours dans l'ordre du nœud à supprimer, remplacez la valeur du nœud à supprimer supprimé avec la valeur du nœud successeur, puis Supprimer les nœuds successeurs.
Problèmes avec Analyse approfondie de limplémentation Java des arbres rouge-noir (photo)
Le principal problème avec Analyse approfondie de limplémentation Java des arbres rouge-noir (photo) est que les nombres feront basculer l'arbre lorsqu'il est inséré. L'ordre entraînera une hauteur de l'arbre différente, et la hauteur de l'arbre affecte directement l'efficacité de la recherche de l'arbre. La hauteur idéale est logN. Dans le pire des cas, tous les nœuds sont sur une ligne diagonale et la hauteur d'un tel arbre est N.
RBTree
Basé sur les problèmes existants de Analyse approfondie de limplémentation Java des arbres rouge-noir (photo), un nouvel arbre - Balanced Binary Search Tree (Balanced Analyse approfondie de limplémentation Java des arbres rouge-noir (photo)) a été créé. Lors de l'insertion et de la suppression, l'arbre équilibré maintiendra la hauteur à logN grâce aux opérations de rotation. Deux arbres équilibrés représentatifs sont les arbres AVL et les arbres rouge-noir. En raison de la mise en œuvre compliquée et des mauvaises performances d'insertion et de suppression de l'arborescence AVL, son application dans l'environnement réel n'est pas aussi bonne que l'arborescence rouge-noir.
Red-Black Tree (ci-après dénommé RBTree) possède un large éventail d'applications pratiques, telles que le planificateur tout à fait équitable du noyau Linux, des minuteries de haute précision, des systèmes de fichiers ext3, etc., dans divers langages Bibliothèques de fonctions telles que TreeMap et TreeSet de Java, map C STL, multimap, multiset, etc.
RBTree est également l'une des structures de données persistantes les plus couramment utilisées dans les langages fonctionnels et joue également un rôle important dans la géométrie computationnelle. Il convient de mentionner que les performances de l'implémentation de HashMap dans Java 8 ont été améliorées en remplaçant les listes chaînées par RBTree.
Définition de RBTree
La définition de RBTree est la suivante :
Tout nœud a une couleur, noire ou rouge
Le nœud racine est noir
Il ne peut pas y avoir deux nœuds rouges consécutifs entre les nœuds parent et enfant
N'importe quel nœud vers le bas Pour parcourir les nœuds feuilles de ses descendants, le nombre de nœuds noirs passés doit être égal
Les nœuds vides sont considérés comme noirs
Structure des données Il s'exprime comme suit :
class Node<T>{
public T value;
public Node<T> parent;
public boolean isRed;
public Node<T> left;
public Node<T> right;
}RBTree est toujours un arbre Analyse approfondie de limplémentation Java des arbres rouge-noir (photo) en théorie, mais il maintiendra l'équilibre de l'arbre lors de l'insertion et de la suppression d'opérations Analyse approfondie de limplémentation Java des arbres rouge-noir (photo), c'est-à-dire en garantissant que la hauteur de l'arbre est [logN,logN 1 ] (Théoriquement, dans les cas extrêmes, la hauteur de RBTree peut atteindre 2*logN, mais en pratique c'est difficile à rencontrer). De cette façon, la complexité temporelle de recherche de RBTree reste toujours à O(logN) et est proche du Analyse approfondie de limplémentation Java des arbres rouge-noir (photo) idéal. La complexité temporelle des opérations de suppression et d'insertion de RBTree est également O(logN). L'opération de recherche de RBTree est l'opération de recherche de Analyse approfondie de limplémentation Java des arbres rouge-noir (photo).
Opération de rotation de RBTree
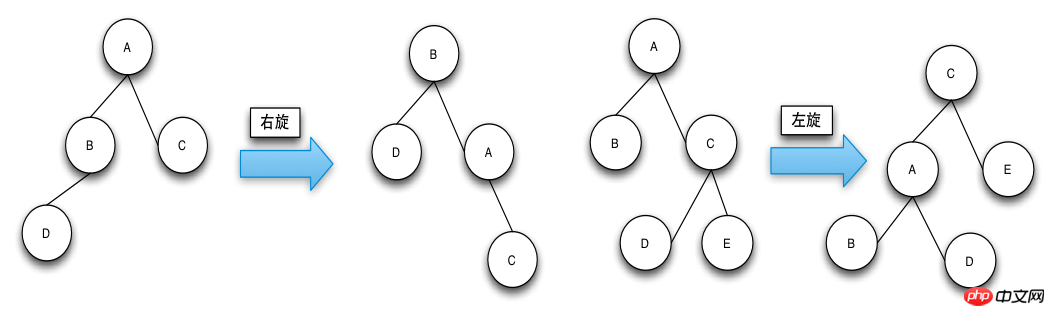
Le but de l'opération de rotation (Rotate) est de rendre la couleur du nœud conforme à la définition et d'équilibrer la hauteur de RBTree.
La rotation est divisée en rotation à gauche (rotation à gauche) et rotation à droite (rotation à droite). La façon de distinguer la rotation à gauche et la rotation à droite est la suivante : le nœud à faire pivoter monte à partir du à gauche vers le nœud parent, ce qui correspond à une rotation à droite, et le nœud à faire pivoter se déplace de la droite vers le nœud parent, c'est un virage à gauche.
Opération de recherche RBTree
L'opération de recherche RBTree est la même que l'opération de recherche Analyse approfondie de limplémentation Java des arbres rouge-noir (photo). Veuillez vous référer au code d'opération de recherche de Analyse approfondie de limplémentation Java des arbres rouge-noir (photo).
Opération d'insertion de RBTree
La méthode d'insertion de RBTree est la même que celle de Analyse approfondie de limplémentation Java des arbres rouge-noir (photo) Cependant, après l'insertion, l'arbre peut être déséquilibré. Dans ce cas, l'arbre doit être pivoté et coloré. fix (appelé ici correctif d'insertion) afin qu'il soit conforme à la définition de RBTree.
Le nœud nouvellement inséré est rouge. Si l'opération de réparation par insertion rencontre un nœud parent dont la couleur est noire, l'opération de réparation se termine. En d’autres termes, l’opération de réparation ne doit être insérée que lorsque le nœud parent est un nœud rouge.
L'opération de réparation par insertion est divisée selon les trois situations suivantes, et les nœuds parents des nœuds nouvellement insérés sont tous rouges :
Le nœud oncle est également rouge.
Le nœud oncle est vide et le nœud grand-parent, le nœud parent et le nouveau nœud sont sur une ligne diagonale.
Le nœud oncle est vide et le nœud grand-parent, le nœud parent et le nouveau nœud ne sont pas sur une barre oblique.
Opération d'insertion-cas 1
L'opération du cas 1 consiste à permuter les couleurs du nœud parent, du nœud oncle et du nœud grand-parent, ce qui est conforme à la définition de Arbre RBT. C'est-à-dire qu'un degré élevé d'équilibre est maintenu et que la couleur après réparation est également conforme aux troisième et quatrième éléments définis par RBTree. Dans la figure ci-dessous, le nœud A devient un nouveau nœud une fois l'opération terminée. Si le nœud parent du nœud A n'est pas noir, poursuivez l'opération de réparation.
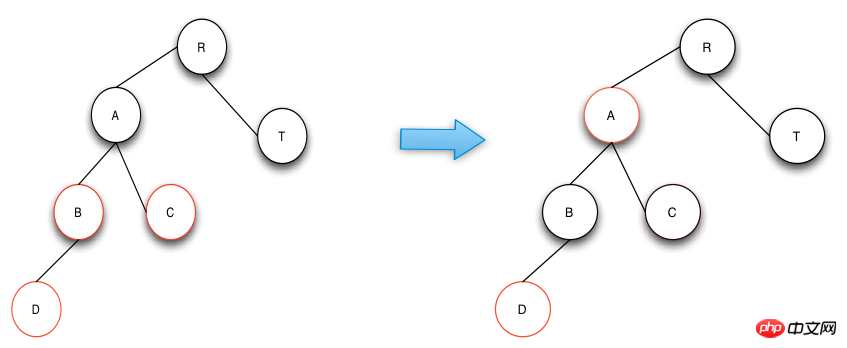
Opération d'insertion-cas 2
L'opération du cas 2 consiste à faire pivoter vers la droite le nœud B et à échanger des couleurs avec le nœud parent A. Grâce à cette opération de réparation, la hauteur et la couleur du RBTree sont conformes à la définition de l'arbre rouge-noir. Si les nœuds B et C sont tous deux des nœuds droits, modifiez simplement l'opération en rotation à gauche.
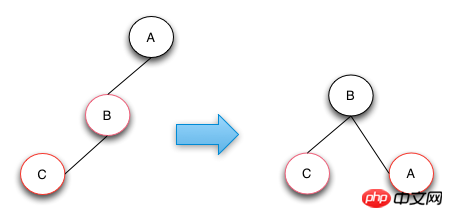
Opération d'insertion-cas 3
L'opération du cas 3 consiste à faire pivoter le nœud C vers la gauche, le convertissant ainsi du cas 3 au cas 2, et puis pour Effectuer simplement le traitement de l'opération dans le cas 2. L'opération du cas 2 effectue une opération de virage à droite et un échange de couleurs pour atteindre l'objectif. Si la structure de l'arborescence est la structure miroir de la figure ci-dessous, il vous suffit de changer la rotation à gauche correspondante en rotation à droite et la rotation à droite en rotation à gauche.
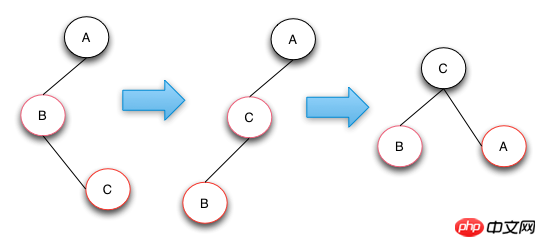
Résumé de l'opération d'insertion
L'opération de réparation après insertion est une opération de retour en arrière vers le nœud racine une fois que les nœuds impliqués sont conformes au rouge-. arbre noir Définition, l'opération de réparation est terminée. La raison du retour en arrière vers le haut est que l'opération du cas 1 changera la couleur du nœud parent, du nœud oncle et du nœud grand-père, ce qui peut entraîner un déséquilibre du nœud grand-père (définition 3 de l'arbre rouge-noir). À ce stade, il est nécessaire d'ajuster le nœud grand-père comme point de départ (retour en arrière vers le haut).
Si le nœud grand-père rencontre toujours son problème de couleur grand-père après ajustement, l'opération continuera à revenir en arrière jusqu'à ce que le nœud racine soit toujours noir. Dans le processus de traçage ascendant, des ajustements sont effectués pour les trois situations insérées. Jusqu’à ce que la définition d’un arbre rouge-noir soit remplie. Jusqu'à ce que tous les nœuds impliqués répondent à la définition d'un arbre rouge-noir, l'opération de réparation se termine.
Si l'opération correspondante dans les 3 situations ci-dessus se trouve sur le sous-arbre de droite, effectuez simplement l'opération miroir correspondante.
Opération de suppression de RBTree
La première chose que vous devez faire pour l'opération de suppression est également l'opération de suppression de Analyse approfondie de limplémentation Java des arbres rouge-noir (photo). L'opération de suppression supprimera le nœud correspondant. S'il s'agit d'un nœud feuille, il. sera supprimé directement. S'il s'agit d'un nœud non-feuille, il sera supprimé. Remplacez la position du nœud à supprimer par le nœud successeur correspondant du parcours dans l'ordre. Après la suppression, vous devez effectuer une opération de suppression et de réparation pour rendre l'arbre conforme à la définition d'un arbre rouge-noir, et la hauteur de l'arbre rouge-noir qui répond à la définition est équilibrée.
L'opération de suppression et de réparation est terminée lorsque le nœud supprimé est un nœud rouge ou atteint le nœud racine.
L'opération de suppression et de réparation sert uniquement à supprimer les nœuds noirs. Lorsque les nœuds noirs sont supprimés, l'arborescence entière ne sera pas conforme à la quatrième définition de RBTree. Ce qu'il faut faire, c'est seconder les nœuds noirs des nœuds frères et sœurs. Si les nœuds frères n'ont pas de nœuds noirs à emprunter, nous ne pouvons que remonter et soustraire un du nombre de nœuds noirs à chaque niveau pour obtenir le tout. arbre conforme à la définition du nœud rouge.
L'idée générale de l'opération de suppression est d'emprunter des nœuds noirs aux nœuds frères pour maintenir un équilibre local dans l'arbre. Si l'équilibre local est atteint, cela dépend si l'arbre global est équilibré. s'il est déséquilibré, il sera ajusté à la hausse rétrospectivement.
L'opération de suppression et de réparation est divisée en quatre situations (après suppression du nœud noir) :
Le nœud frère du nœud à supprimer est un nœud rouge.
Les nœuds frères du nœud à supprimer sont des nœuds noirs, et les nœuds enfants des nœuds frères sont tous noirs.
Le nœud frère du nœud à ajuster est un nœud noir, et le nœud enfant gauche du nœud frère est rouge et le nœud droit est noir (le nœud frère est sur le à droite). Si le nœud frère est à gauche, le nœud enfant droit du nœud frère est rouge et le nœud gauche est noir.
待调整的节点的兄弟节点是黑色的节点,且右子节点是是红色的(兄弟节点在右边),如果兄弟节点在左边,则就是对应的就是左节点是红色的。
删除操作-case 1
由于兄弟节点是红色节点的时候,无法借调黑节点,所以需要将兄弟节点提升到父节点,由于兄弟节点是红色的,根据RBTree的定义,兄弟节点的子节点是黑色的,就可以从它的子节点借调了。
case 1这样转换之后就会变成后面的case 2,case 3,或者case 4进行处理了。上升操作需要对C做一个左旋操作,如果是镜像结构的树只需要做对应的右旋操作即可。
之所以要做case 1操作是因为兄弟节点是红色的,无法借到一个黑节点来填补删除的黑节点。
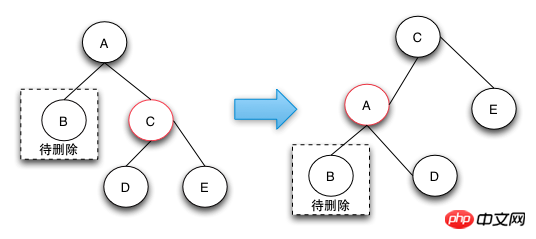
删除操作-case 2
case 2的删除操作是由于兄弟节点可以消除一个黑色节点,因为兄弟节点和兄弟节点的子节点都是黑色的,所以可以将兄弟节点变红,这样就可以保证树的局部的颜色符合定义了。这个时候需要将父节点A变成新的节点,继续向上调整,直到整颗树的颜色符合RBTree的定义为止。
case 2这种情况下之所以要将兄弟节点变红,是因为如果把兄弟节点借调过来,会导致兄弟的结构不符合RBTree的定义,这样的情况下只能是将兄弟节点也变成红色来达到颜色的平衡。当将兄弟节点也变红之后,达到了局部的平衡了,但是对于祖父节点来说是不符合定义4的。这样就需要回溯到父节点,接着进行修复操作。
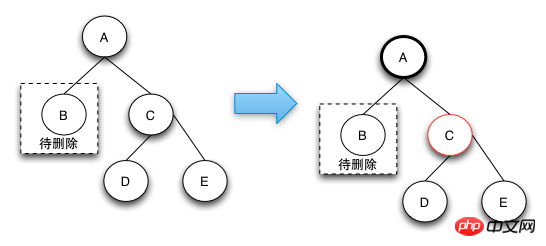
删除操作-case 3
case 3的删除操作是一个中间步骤,它的目的是将左边的红色节点借调过来,这样就可以转换成case 4状态了,在case 4状态下可以将D,E节点都阶段过来,通过将两个节点变成黑色来保证红黑树的整体平衡。
之所以说case-3是一个中间状态,是因为根据红黑树的定义来说,下图并不是平衡的,他是通过case 2操作完后向上回溯出现的状态。之所以会出现case 3和后面的case 4的情况,是因为可以通过借用侄子节点的红色,变成黑色来符合红黑树定义4.
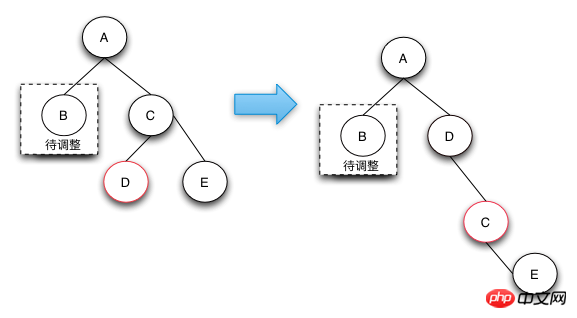
删除操作-case 4
Case 4的操作是真正的节点借调操作,通过将兄弟节点以及兄弟节点的右节点借调过来,并将兄弟节点的右子节点变成红色来达到借调两个黑节点的目的,这样的话,整棵树还是符合RBTree的定义的。
Case 4这种情况的发生只有在待删除的节点的兄弟节点为黑,且子节点不全部为黑,才有可能借调到两个节点来做黑节点使用,从而保持整棵树都符合红黑树的定义。
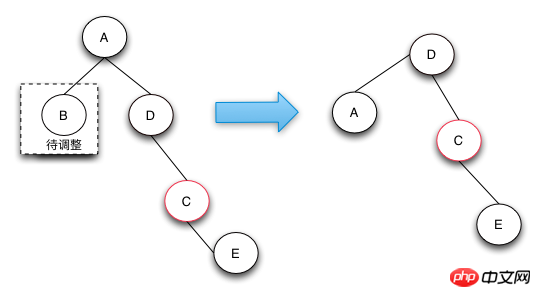
删除操作的总结
红黑树的删除操作是最复杂的操作,复杂的地方就在于当删除了黑色节点的时候,如何从兄弟节点去借调节点,以保证树的颜色符合定义。由于红色的兄弟节点是没法借调出黑节点的,这样只能通过选择操作让他上升到父节点,而由于它是红节点,所以它的子节点就是黑的,可以借调。
对于兄弟节点是黑色节点的可以分成3种情况来处理,当所以的兄弟节点的子节点都是黑色节点时,可以直接将兄弟节点变红,这样局部的红黑树颜色是符合定义的。但是整颗树不一定是符合红黑树定义的,需要往上追溯继续调整。
对于兄弟节点的子节点为左红右黑或者 (全部为红,右红左黑)这两种情况,可以先将前面的情况通过选择转换为后一种情况,在后一种情况下,因为兄弟节点为黑,兄弟节点的右节点为红,可以借调出两个节点出来做黑节点,这样就可以保证删除了黑节点,整棵树还是符合红黑树的定义的,因为黑色节点的个数没有改变。
红黑树的删除操作是遇到删除的节点为红色,或者追溯调整到了root节点,这时删除的修复操作完毕。
RBTree的Java实现
public class RBTreeNode<T extends Comparable<T>> {
private T value;//node value
private RBTreeNode<T> left;//left child pointer
private RBTreeNode<T> right;//right child pointer
private RBTreeNode<T> parent;//parent pointer
private boolean red;//color is red or not red
public RBTreeNode(){}
public RBTreeNode(T value){this.value=value;}
public RBTreeNode(T value,boolean isRed){this.value=value;this.red = isRed;}
public T getValue() {
return value;
}
void setValue(T value) {
this.value = value;
}
RBTreeNode<T> getLeft() {
return left;
}
void setLeft(RBTreeNode<T> left) {
this.left = left;
}
RBTreeNode<T> getRight() {
return right;
}
void setRight(RBTreeNode<T> right) {
this.right = right;
}
RBTreeNode<T> getParent() {
return parent;
}
void setParent(RBTreeNode<T> parent) {
this.parent = parent;
}
boolean isRed() {
return red;
}
boolean isBlack(){
return !red;
}
/**
* is leaf node
**/
boolean isLeaf(){
return left==null && right==null;
}
void setRed(boolean red) {
this.red = red;
}
void makeRed(){
red=true;
}
void makeBlack(){
red=false;
}
@Override
public String toString(){
return value.toString();
}
}
public class RBTree<T extends Comparable<T>> {
private final RBTreeNode<T> root;
//node number
private java.util.concurrent.atomic.AtomicLong size =
new java.util.concurrent.atomic.AtomicLong(0);
//in overwrite mode,all node's value can not has same value
//in non-overwrite mode,node can have same value, suggest don't use non-overwrite mode.
private volatile boolean overrideMode=true;
public RBTree(){
this.root = new RBTreeNode<T>();
}
public RBTree(boolean overrideMode){
this();
this.overrideMode=overrideMode;
}
public boolean isOverrideMode() {
return overrideMode;
}
public void setOverrideMode(boolean overrideMode) {
this.overrideMode = overrideMode;
}
/**
* number of tree number
* @return
*/
public long getSize() {
return size.get();
}
/**
* get the root node
* @return
*/
private RBTreeNode<T> getRoot(){
return root.getLeft();
}
/**
* add value to a new node,if this value exist in this tree,
* if value exist,it will return the exist value.otherwise return null
* if override mode is true,if value exist in the tree,
* it will override the old value in the tree
*
* @param value
* @return
*/
public T addNode(T value){
RBTreeNode<T> t = new RBTreeNode<T>(value);
return addNode(t);
}
/**
* find the value by give value(include key,key used for search,
* other field is not used,@see compare method).if this value not exist return null
* @param value
* @return
*/
public T find(T value){
RBTreeNode<T> dataRoot = getRoot();
while(dataRoot!=null){
int cmp = dataRoot.getValue().compareTo(value);
if(cmp<0){
dataRoot = dataRoot.getRight();
}else if(cmp>0){
dataRoot = dataRoot.getLeft();
}else{
return dataRoot.getValue();
}
}
return null;
}
/**
* remove the node by give value,if this value not exists in tree return null
* @param value include search key
* @return the value contain in the removed node
*/
public T remove(T value){
RBTreeNode<T> dataRoot = getRoot();
RBTreeNode<T> parent = root;
while(dataRoot!=null){
int cmp = dataRoot.getValue().compareTo(value);
if(cmp<0){
parent = dataRoot;
dataRoot = dataRoot.getRight();
}else if(cmp>0){
parent = dataRoot;
dataRoot = dataRoot.getLeft();
}else{
if(dataRoot.getRight()!=null){
RBTreeNode<T> min = removeMin(dataRoot.getRight());
//x used for fix color balance
RBTreeNode<T> x = min.getRight()==null ? min.getParent() : min.getRight();
boolean isParent = min.getRight()==null;
min.setLeft(dataRoot.getLeft());
setParent(dataRoot.getLeft(),min);
if(parent.getLeft()==dataRoot){
parent.setLeft(min);
}else{
parent.setRight(min);
}
setParent(min,parent);
boolean curMinIsBlack = min.isBlack();
//inherit dataRoot's color
min.setRed(dataRoot.isRed());
if(min!=dataRoot.getRight()){
min.setRight(dataRoot.getRight());
setParent(dataRoot.getRight(),min);
}
//remove a black node,need fix color
if(curMinIsBlack){
if(min!=dataRoot.getRight()){
fixRemove(x,isParent);
}else if(min.getRight()!=null){
fixRemove(min.getRight(),false);
}else{
fixRemove(min,true);
}
}
}else{
setParent(dataRoot.getLeft(),parent);
if(parent.getLeft()==dataRoot){
parent.setLeft(dataRoot.getLeft());
}else{
parent.setRight(dataRoot.getLeft());
}
//current node is black and tree is not empty
if(dataRoot.isBlack() && !(root.getLeft()==null)){
RBTreeNode<T> x = dataRoot.getLeft()==null
? parent :dataRoot.getLeft();
boolean isParent = dataRoot.getLeft()==null;
fixRemove(x,isParent);
}
}
setParent(dataRoot,null);
dataRoot.setLeft(null);
dataRoot.setRight(null);
if(getRoot()!=null){
getRoot().setRed(false);
getRoot().setParent(null);
}
size.decrementAndGet();
return dataRoot.getValue();
}
}
return null;
}
/**
* fix remove action
* @param node
* @param isParent
*/
private void fixRemove(RBTreeNode<T> node,boolean isParent){
RBTreeNode<T> cur = isParent ? null : node;
boolean isRed = isParent ? false : node.isRed();
RBTreeNode<T> parent = isParent ? node : node.getParent();
while(!isRed && !isRoot(cur)){
RBTreeNode<T> sibling = getSibling(cur,parent);
//sibling is not null,due to before remove tree color is balance
//if cur is a left node
boolean isLeft = parent.getRight()==sibling;
if(sibling.isRed() && !isLeft){//case 1
//cur in right
parent.makeRed();
sibling.makeBlack();
rotateRight(parent);
}else if(sibling.isRed() && isLeft){
//cur in left
parent.makeRed();
sibling.makeBlack();
rotateLeft(parent);
}else if(isBlack(sibling.getLeft()) && isBlack(sibling.getRight())){//case 2
sibling.makeRed();
cur = parent;
isRed = cur.isRed();
parent=parent.getParent();
}else if(isLeft && !isBlack(sibling.getLeft())
&& isBlack(sibling.getRight())){//case 3
sibling.makeRed();
sibling.getLeft().makeBlack();
rotateRight(sibling);
}else if(!isLeft && !isBlack(sibling.getRight())
&& isBlack(sibling.getLeft()) ){
sibling.makeRed();
sibling.getRight().makeBlack();
rotateLeft(sibling);
}else if(isLeft && !isBlack(sibling.getRight())){//case 4
sibling.setRed(parent.isRed());
parent.makeBlack();
sibling.getRight().makeBlack();
rotateLeft(parent);
cur=getRoot();
}else if(!isLeft && !isBlack(sibling.getLeft())){
sibling.setRed(parent.isRed());
parent.makeBlack();
sibling.getLeft().makeBlack();
rotateRight(parent);
cur=getRoot();
}
}
if(isRed){
cur.makeBlack();
}
if(getRoot()!=null){
getRoot().setRed(false);
getRoot().setParent(null);
}
}
//get sibling node
private RBTreeNode<T> getSibling(RBTreeNode<T> node,RBTreeNode<T> parent){
parent = node==null ? parent : node.getParent();
if(node==null){
return parent.getLeft()==null ? parent.getRight() : parent.getLeft();
}
if(node==parent.getLeft()){
return parent.getRight();
}else{
return parent.getLeft();
}
}
private boolean isBlack(RBTreeNode<T> node){
return node==null || node.isBlack();
}
private boolean isRoot(RBTreeNode<T> node){
return root.getLeft() == node && node.getParent()==null;
}
/**
* find the successor node
* @param node current node's right node
* @return
*/
private RBTreeNode<T> removeMin(RBTreeNode<T> node){
//find the min node
RBTreeNode<T> parent = node;
while(node!=null && node.getLeft()!=null){
parent = node;
node = node.getLeft();
}
//remove min node
if(parent==node){
return node;
}
parent.setLeft(node.getRight());
setParent(node.getRight(),parent);
//don't remove right pointer,it is used for fixed color balance
//node.setRight(null);
return node;
}
private T addNode(RBTreeNode<T> node){
node.setLeft(null);
node.setRight(null);
node.setRed(true);
setParent(node,null);
if(root.getLeft()==null){
root.setLeft(node);
//root node is black
node.setRed(false);
size.incrementAndGet();
}else{
RBTreeNode<T> x = findParentNode(node);
int cmp = x.getValue().compareTo(node.getValue());
if(this.overrideMode && cmp==0){
T v = x.getValue();
x.setValue(node.getValue());
return v;
}else if(cmp==0){
//value exists,ignore this node
return x.getValue();
}
setParent(node,x);
if(cmp>0){
x.setLeft(node);
}else{
x.setRight(node);
}
fixInsert(node);
size.incrementAndGet();
}
return null;
}
/**
* find the parent node to hold node x,if parent value equals x.value return parent.
* @param x
* @return
*/
private RBTreeNode<T> findParentNode(RBTreeNode<T> x){
RBTreeNode<T> dataRoot = getRoot();
RBTreeNode<T> child = dataRoot;
while(child!=null){
int cmp = child.getValue().compareTo(x.getValue());
if(cmp==0){
return child;
}
if(cmp>0){
dataRoot = child;
child = child.getLeft();
}else if(cmp<0){
dataRoot = child;
child = child.getRight();
}
}
return dataRoot;
}
/**
* red black tree insert fix.
* @param x
*/
private void fixInsert(RBTreeNode<T> x){
RBTreeNode<T> parent = x.getParent();
while(parent!=null && parent.isRed()){
RBTreeNode<T> uncle = getUncle(x);
if(uncle==null){//need to rotate
RBTreeNode<T> ancestor = parent.getParent();
//ancestor is not null due to before before add,tree color is balance
if(parent == ancestor.getLeft()){
boolean isRight = x == parent.getRight();
if(isRight){
rotateLeft(parent);
}
rotateRight(ancestor);
if(isRight){
x.setRed(false);
parent=null;//end loop
}else{
parent.setRed(false);
}
ancestor.setRed(true);
}else{
boolean isLeft = x == parent.getLeft();
if(isLeft){
rotateRight(parent);
}
rotateLeft(ancestor);
if(isLeft){
x.setRed(false);
parent=null;//end loop
}else{
parent.setRed(false);
}
ancestor.setRed(true);
}
}else{//uncle is red
parent.setRed(false);
uncle.setRed(false);
parent.getParent().setRed(true);
x=parent.getParent();
parent = x.getParent();
}
}
getRoot().makeBlack();
getRoot().setParent(null);
}
/**
* get uncle node
* @param node
* @return
*/
private RBTreeNode<T> getUncle(RBTreeNode<T> node){
RBTreeNode<T> parent = node.getParent();
RBTreeNode<T> ancestor = parent.getParent();
if(ancestor==null){
return null;
}
if(parent == ancestor.getLeft()){
return ancestor.getRight();
}else{
return ancestor.getLeft();
}
}
private void rotateLeft(RBTreeNode<T> node){
RBTreeNode<T> right = node.getRight();
if(right==null){
throw new java.lang.IllegalStateException("right node is null");
}
RBTreeNode<T> parent = node.getParent();
node.setRight(right.getLeft());
setParent(right.getLeft(),node);
right.setLeft(node);
setParent(node,right);
if(parent==null){//node pointer to root
//right raise to root node
root.setLeft(right);
setParent(right,null);
}else{
if(parent.getLeft()==node){
parent.setLeft(right);
}else{
parent.setRight(right);
}
//right.setParent(parent);
setParent(right,parent);
}
}
private void rotateRight(RBTreeNode<T> node){
RBTreeNode<T> left = node.getLeft();
if(left==null){
throw new java.lang.IllegalStateException("left node is null");
}
RBTreeNode<T> parent = node.getParent();
node.setLeft(left.getRight());
setParent(left.getRight(),node);
left.setRight(node);
setParent(node,left);
if(parent==null){
root.setLeft(left);
setParent(left,null);
}else{
if(parent.getLeft()==node){
parent.setLeft(left);
}else{
parent.setRight(left);
}
setParent(left,parent);
}
}
private void setParent(RBTreeNode<T> node,RBTreeNode<T> parent){
if(node!=null){
node.setParent(parent);
if(parent==root){
node.setParent(null);
}
}
}
/**
* debug method,it used print the given node and its children nodes,
* every layer output in one line
* @param root
*/
public void printTree(RBTreeNode<T> root){
java.util.LinkedList<RBTreeNode<T>> queue =new java.util.LinkedList<RBTreeNode<T>>();
java.util.LinkedList<RBTreeNode<T>> queue2 =new java.util.LinkedList<RBTreeNode<T>>();
if(root==null){
return ;
}
queue.add(root);
boolean firstQueue = true;
while(!queue.isEmpty() || !queue2.isEmpty()){
java.util.LinkedList<RBTreeNode<T>> q = firstQueue ? queue : queue2;
RBTreeNode<T> n = q.poll();
if(n!=null){
String pos = n.getParent()==null ? "" : ( n == n.getParent().getLeft()
? " LE" : " RI");
String pstr = n.getParent()==null ? "" : n.getParent().toString();
String cstr = n.isRed()?"R":"B";
cstr = n.getParent()==null ? cstr : cstr+" ";
System.out.print(n+"("+(cstr)+pstr+(pos)+")"+"\t");
if(n.getLeft()!=null){
(firstQueue ? queue2 : queue).add(n.getLeft());
}
if(n.getRight()!=null){
(firstQueue ? queue2 : queue).add(n.getRight());
}
}else{
System.out.println();
firstQueue = !firstQueue;
}
}
}
public static void main(String[] args) {
RBTree<String> bst = new RBTree<String>();
bst.addNode("d");
bst.addNode("d");
bst.addNode("c");
bst.addNode("c");
bst.addNode("b");
bst.addNode("f");
bst.addNode("a");
bst.addNode("e");
bst.addNode("g");
bst.addNode("h");
bst.remove("c");
bst.printTree(bst.getRoot());
}
}代码调试的时候,printTree输出格式如下:
d(B) b(B d LE) g(R d RI) a(R b LE) e(B g LE) h(B g RI) f(R e RI)
括号左边表示元素的内容。括号内的第一个元素表示颜色,B表示black,R表示red;第二个元素表示父元素的值;第三个元素表示左右,LE表示在父元素的左边。RI表示在父元素的右边。
第一个元素d是root节点,由于它没有父节点,所以括号内只有一个元素。
总结
作为平衡二叉查找树里面众多的实现之一,红黑树无疑是最简洁、实现最为简单的。红黑树通过引入颜色的概念,通过颜色这个约束条件的使用来保持树的高度平衡。作为平衡二叉查找树,旋转是一个必不可少的操作。通过旋转可以降低树的高度,在红黑树里面还可以转换颜色。
红黑树里面的插入和删除的操作比较难理解,这时要注意记住一点:操作之前红黑树是平衡的,颜色是符合定义的。在操作的时候就需要向兄弟节点、父节点、侄子节点借调和互换颜色,要达到这个目的,就需要不断的进行旋转。所以红黑树的插入删除操作需要不停的旋转,一旦借调了别的节点,删除和插入的节点就会达到局部的平衡(局部符合红黑树的定义),但是被借调的节点就不会平衡了,这时就需要以被借调的节点为起点继续进行调整,直到整棵树都是平衡的。在整个修复的过程中,插入具体的分为3种情况,删除分为4种情况。
整个红黑树的查找,插入和删除都是O(logN)的,原因就是整个红黑树的高度是logN,查找从根到叶,走过的路径是树的高度,删除和插入操作是从叶到根的,所以经过的路径都是logN。
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Comment injecter des dépendances dans des objets auto-instanciés au printemps ?
- Où devriez-vous placer vos JFrames ?
- Attentes implicites ou explicites dans Selenium-WebDriver : laquelle devriez-vous choisir ?
- Comment ajouter dynamiquement des fichiers au chemin de classe Java lors de l'exécution ?
- Débogage d'API : meilleures pratiques pour récupérer des données de test à partir d'une base de données

