Comment implémenter le tas binaire en Python

Le tas binaire est un type spécial de tas. Le tas binaire est un arbre binaire complet (arbre binaire) ou un arbre binaire approximativement complet (arbre binaire). Il existe deux types de tas binaires : max-heap et min-heap. Max tas : la valeur clé du nœud parent est toujours supérieure ou égale à la valeur clé de tout nœud enfant ; min tas : la valeur clé du nœud parent est toujours inférieure ou égale à la valeur clé de tout nœud enfant.

Implémentation du tas binaire de la file d'attente prioritaire

Dans le chapitre précédent, nous avons appris la structure de données du "premier entré, premier sorti" (FIFO) : file d'attente (Queue). Il existe une variante de file d'attente appelée « file d'attente prioritaire » (Priority Queue). L'opération de retrait de la file d'attente (Dequeue) de la file d'attente prioritaire est la même que celle de la file d'attente, et elle est retirée de la file d'attente de la tête de la file d'attente. Mais à l'intérieur de la file d'attente prioritaire, l'ordre des éléments est déterminé par "Priorité" : les éléments de haute priorité sont en début de file d'attente, tandis que les éléments de faible priorité sont à l'arrière. De cette façon, l'opération de mise en file d'attente (Enqueue) de la file d'attente prioritaire est plus compliquée et les éléments doivent être mis en file d'attente autant que possible en fonction de la priorité. Nous découvrirons que les files d’attente prioritaires constituent une structure de données utile pour les algorithmes graphiques dans la section suivante.

On pense naturellement à utiliser des algorithmes de tri et des files d'attente pour mettre en place des files d'attente prioritaires. Cependant, la complexité temporelle de l'insertion d'un élément dans la liste est O(n), et la complexité temporelle du tri de la liste est O(nlogn). Nous pouvons utiliser d'autres méthodes pour réduire la complexité temporelle. Une manière classique d'implémenter une file d'attente prioritaire consiste à utiliser un tas binaire (Binary Heap). Le tas binaire peut maintenir la complexité de la mise en file d'attente et du retrait de la file d'attente prioritaire à O(logn).

La chose intéressante à propos du tas binaire est que sa structure logique est comme un arbre binaire, mais il est implémenté avec des listes non imbriquées. Il existe deux types de tas binaires : celui avec la plus petite valeur de clé toujours placé en tête de la file d'attente est appelé « tas minimum (min heap) » ; à l'inverse, celui avec la plus grande valeur de clé toujours placé en tête ; de la file d'attente est appelé "tas maximum (max heap) )". Dans cette section, nous utilisons min-heap.

Opérations du tas binaire

Les opérations de base du tas binaire sont définies comme suit :

1. BinaryHeap() : Créer un objet tas binaire vide

2. insert(k) : Ajouter de nouveaux éléments au tas

3. findMin() : Renvoie le plus petit élément du tas item, l'élément min reste dans le tas

4. delMin() : Renvoie l'élément min dans le tas, tout en le retirant du tas

5. isEmpty() : Renvoie si le tas est vide

6. size() : Renvoie le nombre de nœuds dans le tas

7. buildHeap(list) : À partir d'un conteneur Créez un nouveau tas à partir de la liste des nœuds

Le code ci-dessous est un exemple de tas binaire. Vous pouvez voir que quel que soit l'ordre dans lequel nous ajoutons des éléments au tas, le plus petit élément est supprimé à chaque fois. Nous mettrons en œuvre ce processus ensuite.

from pythonds.trees.binheap import BinHeap

bh = BinHeap()
bh.insert(5)
bh.insert(7)
bh.insert(3)
bh.insert(11)

print(bh.delMin())

print(bh.delMin())

print(bh.delMin())

print(bh.delMin())

Afin de mieux implémenter le tas, nous utilisons un arbre binaire. Il faut toujours maintenir « l'équilibre » de l'arbre binaire, et il faut toujours garder le fonctionnement sur l'échelle logarithmique. Un arbre binaire équilibré a le même nombre de nœuds enfants dans les sous-arbres gauche et droit du nœud racine. Dans la mise en œuvre du tas, nous utilisons la structure d'un « arbre binaire complet » pour atteindre approximativement « l'équilibre ». Un arbre binaire complet signifie que chaque arbre de nœuds interne atteint sa valeur maximale, sauf que le dernier niveau ne peut manquer que de plusieurs nœuds à droite. La figure 1 montre un arbre binaire complet.

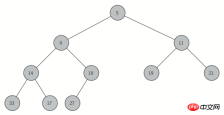
Figure 1 : Arbre binaire complet

Fait intéressant, nous pouvons réaliser un arbre complet avec une seule liste. Nous n'avons pas besoin d'utiliser des nœuds, des références ou des listes imbriquées. Car pour un arbre binaire complet, si l'index du nœud dans la liste est p, alors l'index de son nœud enfant gauche est 2p et le nœud droit est 2p 1. Lorsque nous voulons trouver le nœud parent d'un nœud, nous pouvons directement utiliser la division entière de Python. Si un nœud est indexé n dans la liste, alors le nœud parent est indexé n//2 La figure 2 montre un arbre binaire complet et une représentation en liste de l'arbre. Notez la relation 2p et 2p 1 entre le nœud parent et le nœud enfant. La représentation en liste d'un arbre complet combine les propriétés d'un arbre binaire complet, nous permettant de parcourir efficacement un arbre complet à l'aide de méthodes mathématiques simples. Cela nous permet également d'implémenter efficacement des tas binaires.

Propriétés de l'ordre du tas

La façon dont nous stockons les éléments dans le tas dépend de l'ordre du tas. Ce qu'on appelle l'ordre du tas signifie que pour tout nœud x dans le tas, la valeur clé de son nœud parent p est inférieure ou égale à la valeur clé de x. La figure 2 montre un arbre binaire complet avec des propriétés d'ordre de tas.

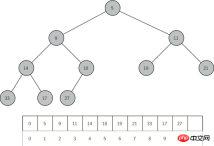
Figure 2 : Arbre complet et sa représentation de liste

Implémentation de l'opération de tas binaire

接下来我们来构造二叉堆。因为可以采用一个列表保存堆的数据，构造函数只需要初始化一个列表和一个currentSize来表示堆当前的大小。Listing 1 所示的是构造二叉堆的 python 代码。注意到二叉堆的heaplist并没有用到，但为了后面代码可以方便地使用整除，我们仍然保留它。

Listing 1

class BinHeap:
  def init(self):
    self.heapList = [0]
    self.currentSize = 0

我们接下来要实现的是insert方法。首先，为了满足“完全二叉树”的性质，新键值应该添加到列表的末尾。然而新键值简单地添加在列表末尾，显然无法满足堆次序。但我们可以通过比较父节点和新加入的元素的方法来重新满足堆次序。如果新加入的元素比父节点要小，可以与父节点互换位置。图 3 所示的是一系列交换操作来使新加入元素“上浮”到正确的位置。

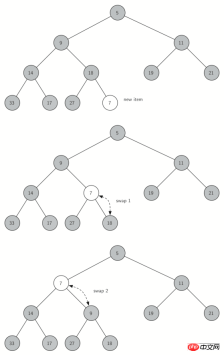
图 3：新节点“上浮”到其正确位置

当我们让一个元素“上浮”时，我们要保证新节点与父节点以及其他兄弟节点之间的堆次序。当然，如果新节点非常小，我们仍然需要将它交换到其他层。事实上，我们需要不断交换，直到到达树的顶端。Listing 2 所示的是“上浮”方法，它把一个新节点“上浮”到其正确位置来满足堆次序。这里很好地体现了我们之前在headlist中没有用到的元素 0 的重要性。这样只需要做简单的整除，将当前节点的下标除以 2，我们就能计算出任何节点的父节点。

在Listing 3 中，我们已经可以写出insert方法的代码。insert里面很大一部分工作是由percUp函数完成的。当树添加新节点时，调用percUp就可以将新节点放到正确的位置上。

Listing 2

def percUp(self,i):
  while i // 2 > 0:
   if self.heapList[i] < self.heapList[i // 2]:
     tmp = self.heapList[i // 2]
     self.heapList[i // 2] = self.heapList[i]
     self.heapList[i] = tmp
   i = i // 2

Listing 3

def insert(self,k):
  self.heapList.append(k)
  self.currentSize = self.currentSize + 1
  self.percUp(self.currentSize)

我们已经写好了insert方法，那再来看看delMin方法。堆次序要求根节点是树中最小的元素，因此很容易找到最小项。比较困难的是移走根节点的元素后如何保持堆结构和堆次序，我们可以分两步走。首先，用最后一个节点来代替根节点。移走最后一个节点保持了堆结构的性质。这么简单的替换，还是会破坏堆次序。那么第二步，将新节点“下沉”来恢复堆次序。图 4 所示的是一系列交换操作来使新节点“下沉”到正确的位置。

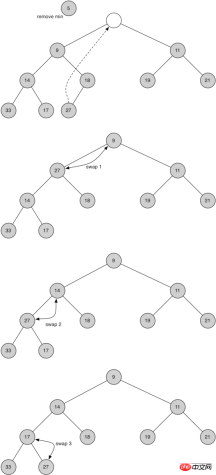
图 4：替换后的根节点下沉

为了保持堆次序，我们需将新的根节点沿着一条路径“下沉”，直到比两个子节点都小。在选择下沉路径时，如果新根节点比子节点大，那么选择较小的子节点与之交换。Listing 4 所示的是新节点下沉所需的percDown和minChild方法的代码。

Listing 4

def percDown(self,i):
  while (i * 2) <= self.currentSize:
    mc = self.minChild(i)
    if self.heapList[i] > self.heapList[mc]:
      tmp = self.heapList[i]
      self.heapList[i] = self.heapList[mc]
      self.heapList[mc] = tmp
    i = mc

def minChild(self,i):
  if i * 2 + 1 > self.currentSize:
    return i * 2
  else:
    if self.heapList[i*2] < self.heapList[i*2+1]:
      return i * 2
    else:
      return i * 2 + 1

Listing 5 所示的是delMin操作的代码。可以看到比较麻烦的地方由一个辅助函数来处理，即percDown。

Listing 5

def delMin(self):
  retval = self.heapList[1]
  self.heapList[1] = self.heapList[self.currentSize]
  self.currentSize = self.currentSize - 1
  self.heapList.pop()
  self.percDown(1)
  return retval

关于二叉堆的最后一部分便是找到从无序列表生成一个“堆”的方法。我们首先想到的是，将无序列表中的每个元素依次插入到堆中。对于一个排好序的列表，我们可以用二分搜索找到合适的位置，然后在下一个位置插入这个键值到堆中，时间复杂度为O(logn)。另外插入一个元素到列表中需要将列表的一些其他元素移动，为新节点腾出位置，时间复杂度为O(n)。因此用insert方法的总开销是O(nlogn)。其实我们能直接将整个列表生成堆，将总开销控制在O(n)。Listing 6 所示的是生成堆的操作。

Listing 6

def buildHeap(self,alist):
  i = len(alist) // 2
  self.currentSize = len(alist)
  self.heapList = [0] + alist[:]
  while (i > 0):
    self.percDown(i)
    i = i - 1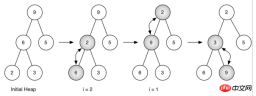

图 5：将列表[ 9, 6, 5, 2, 3]生成一个二叉堆

图 5 所示的是利用buildHeap方法将最开始的树[ 9, 6, 5, 2, 3]中的节点移动到正确的位置时所做的交换操作。尽管我们从树中间开始，然后回溯到根节点，但percDown方法保证了最大子节点总是“下沉”。因为堆是完全二叉树，任何在中间的节点都是叶节点，因此没有子节点。注意，当i=1时，我们从根节点开始下沉，这就需要进行大量的交换操作。可以看到，图 5 最右边的两颗树，首先 9 从根节点的位置移走，移到下一层级之后，percDown进一步检查它此时的子节点，保证它下降到不能再下降为止，即下降到正确的位置。然后进行第二次交换，9 和 3 的交换。由于 9 已经移到了树最底层的层级，便无法进一步交换了。比较一下列表表示法和图 5 所示的树表示法进行的一系列交换还是很有帮助的。

i = 2 [0, 9, 5, 6, 2, 3]
i = 1 [0, 9, 2, 6, 5, 3]
i = 0 [0, 2, 3, 6, 5, 9]

下列所示的代码是完全二叉堆的实现。

def insert(self,k):
   self.heapList.append(k)
   self.currentSize = self.currentSize + 1
   self.percUp(self.currentSize)

  def percDown(self,i):
   while (i * 2) <= self.currentSize:
     mc = self.minChild(i)
     if self.heapList[i] > self.heapList[mc]:
       tmp = self.heapList[i]
       self.heapList[i] = self.heapList[mc]
       self.heapList[mc] = tmp
     i = mc

  def minChild(self,i):
   if i * 2 + 1 > self.currentSize:
     return i * 2
   else:
     if self.heapList[i*2] < self.heapList[i*2+1]:
       return i * 2
     else:
       return i * 2 + 1

  def delMin(self):
   retval = self.heapList[1]
   self.heapList[1] = self.heapList[self.currentSize]
   self.currentSize = self.currentSize - 1

能在O(n)的开销下能生成二叉堆看起来有点不可思议，其证明超出了本书的范围。但是，要理解用O(n)的开销能生成堆的关键是因为logn因子基于树的高度。而对于buildHeap里的许多操作，树的高度比logn要小。

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!