Examiner la "récursivité" à partir de l'utilisation de la mémoire de la classification Infinitus

Dans la classification infinie de PHP, de nombreuses méthodes utilisées sont récursives, mais notre compréhension de la récursivité est encore vague. Ensuite, nous aurons une compréhension approfondie des avantages et des inconvénients de la récursivité afin que chacun puisse la comprendre. de celui-ci.

Qu'est-ce que la récursivité ?

Définition

Récursion (anglais : Récursion), également traduit par récursivité, en mathématiques et en informatique, fait référence à la fonction Méthodes qui utilisent la fonction elle-même dans la définition.

L'analyse étymologique de l'anglais Recursion est simplement "re- (again)" "curs- (venir, arriver)", ce qui signifie récurrence, réapparition à nouveau. La traduction chinoise correspondante « récursion » exprime deux significations : « récursion » + « retour ». Ces deux significations sont l’essence de la pensée récursive. De ce point de vue, la traduction chinoise est plus expressive.

J'ai vu cette analogie encore et encore sur Internet :

Supposons que vous soyez dans une salle de cinéma et que vous vouliez savoir dans quelle rangée vous êtes assis , mais la personne devant vous Il y en a tellement que vous êtes trop paresseux pour compter, alors vous demandez à la personne au premier rang "Dans quelle rangée êtes-vous assis ?", de sorte qu'après la personne devant (nom de code A ) vous répond, vous saurez dans quelle ligne vous vous trouvez - à condition d'en ajouter un à la réponse de A pour déterminer votre ligne. De façon inattendue, A est plus paresseux que vous et il ne veut pas compter, alors il demande également à la personne en face de lui, B : « Dans quelle rangée es-tu assis ? », afin que A puisse savoir dans quelle rangée il se trouve. en suivant les mêmes étapes que vous. Alors B fait la même chose. Jusqu'à ce que le groupe de personnes pose des questions sur la première rangée, la personne au premier rang dit à la personne qui a posé la question "Je suis au premier rang". Finalement, chacun sait dans quelle rangée il se trouve. La différence entre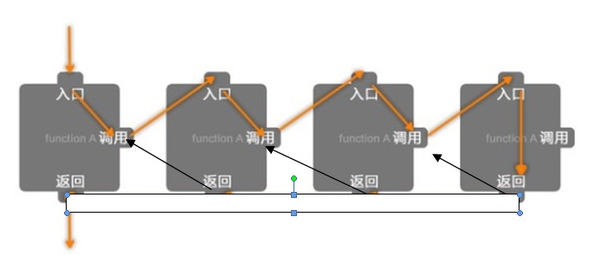

et une boucle

Regardez simplement la définition d'après le wiki ci-dessus, cela semble être très similaire à ce que l'on appelle communément une boucle infinie. Quelle est la différence entre eux ?

La récursion est un mouvement dans le calme, un aller et un retour.
Le cycle est le même mouvement et le même calme, et il n'y a pas de retour.

Par exemple, on vous donne une clé. Vous vous placez devant la porte et demandez combien de portes vous pouvez ouvrir avec cette clé.

Récursion : Vous ouvrez la porte devant vous et voyez une autre porte dans la maison (cette porte peut être de la même taille que la porte ouverte devant (silencieuse), ou elle peut être plus petite (en mouvement)) , vous vous approchez, vous constatez que la clé dans votre main peut toujours l'ouvrir. Vous poussez la porte et constatez qu'il y a une autre porte à l'intérieur. . . , après quelques fois, vous ouvrez une porte devant vous et constatez qu'il n'y a qu'une seule pièce et aucune porte. Vous commencez à revenir de la même manière, et chaque fois que vous retournez dans une pièce, vous la comptez une fois. Lorsque vous atteignez l'entrée, vous pouvez répondre combien de portes vous avez ouvertes avec cette clé.

Boucle : Vous ouvrez la porte devant vous et voyez une autre porte dans la maison, (cette porte peut être de la même taille que la porte ouverte devant (silencieuse), ou elle peut être plus petite (en mouvement) ), Vous vous approchez et constatez que la clé dans votre main peut toujours l'ouvrir. Vous poussez la porte pour l'ouvrir et constatez qu'il y a une autre porte à l'intérieur (si la porte précédente est la même, cette porte est la même. Si la seconde. la porte est plus petite que la première porte, , cette porte est également plus petite que la deuxième porte (le mouvement est le même, soit pas de changement, soit même changement)), vous continuez à ouvrir cette porte. . . , continue comme ça. La personne à l’entrée n’attend jamais que vous reveniez pour lui donner la réponse.

Pensée récursive

La récursion signifie aller (passer) et revenir (revenir).

Plus précisément, pourquoi pouvez-vous « y aller » ?
Le problème qui nécessite une récursion doit être capable d'utiliser la même idée de résolution de problème pour répondre à des questions similaires mais légèrement différentes (la clé dans l'exemple ci-dessus peut ouvrir la serrure de la porte arrière).

Pourquoi puis-je « revenir » ?
Cela nécessite que dans le processus de ces problèmes passant constamment du grand au petit, du proche au lointain, il y ait un point final, un point critique, une ligne de base, et lorsque vous atteignez ce point, vous n'avez plus besoin de allez dans des endroits plus petits ou plus éloignés. Descendez jusqu'au point de départ, puis partez de ce point et revenez au point d'origine.

L'idée de base de la récursivité est de transformer des problèmes à grande échelle en sous-problèmes similaires à petite échelle à résoudre. Lors de l'implémentation d'une fonction, comme la méthode de résolution de gros problèmes et la méthode de résolution de petits problèmes sont souvent la même méthode, la fonction s'appelle elle-même. De plus, la fonction qui résout le problème doit avoir une condition finale évidente, afin qu’une récursion infinie ne se produise pas.

Quand devez-vous utiliser la récursivité ?

Lorsque la définition de certains problèmes elle-même est récursive, il est plus approprié d'utiliser la récursion pour le résoudre.

Les étudiants en informatique sont les plus familiers avec la définition de « arbre » [4,5]. Il existe également quelques définitions, comme factorielle, séquence de Fibonacci [6], etc. L'utilisation de la récursivité pour résoudre ces problèmes résout souvent certains problèmes apparemment « effrayants » en quelques lignes de code seulement. Bien entendu, la question des performances de la récursivité est une autre question. L'allocation de pile et les coûts d'appel de fonction doivent être pris en compte dans des pratiques d'ingénierie spécifiques. Mais si nous discutons maintenant uniquement des pensées récursives, autant les mettre de côté et apprécier la beauté de la récursivité.

---

La récursion simplifie notre façon de penser lors de la résolution de certains problèmes, et le code est plus raffiné et plus facile à lire. Alors, puisque la récursion présente de nombreux avantages, devrions-nous utiliser la récursivité pour résoudre tous les problèmes ? La récursivité n’a-t-elle aucun inconvénient ? Aujourd'hui, nous allons discuter des inconvénients de la récursivité. Lorsqu'il s'agit de récursivité, nous devons faire face à son problème d'efficacité.

Pourquoi la récursivité est-elle inefficace ?

Prenons la séquence de Fibonacci comme exemple. Dans de nombreux manuels ou articles mentionnant la récursivité ou la complexité informatique, le programme de calcul de la séquence de Fibonacci est utilisé comme exemple classique. Si on vous demande maintenant d'écrire une fonction qui calcule le nième nombre de la séquence de Fibonacci en C# le plus rapidement possible (indépendamment des exceptions telles que des paramètres inférieurs à 1 ou un débordement de résultat), je ne sais pas si votre programme correspondra au code suivant Similaire :

public static ulong Fib(ulong n)
{
    return (n == 1 || n == 2) ? 1 : Fib(n - 1) + Fib(n - 2);
}

Ce code doit être considéré comme court et concis (une seule ligne de code d'exécution), intuitif et clair, et très cohérent avec l'esthétique du code de nombreux programmeurs. écrire un tel code pendant les entretiens. Peut-être que je me sentirai toujours secrètement heureux. Mais si vous utilisez ce code pour essayer de calculer Fib(1000), je pense que vous ne serez plus content. Sa durée d'exécution risque de vous rendre fou.

Il semble qu'un beau code ne soit peut-être pas utile si l'efficacité du programme ne peut être acceptée, alors tout le beau code sera vain. Si vous analysez brièvement le flux d'exécution du programme, vous trouverez le problème en prenant le calcul de Fibonacci(5) comme exemple :

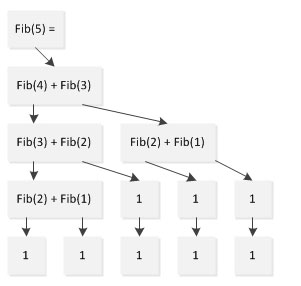
Comme le montre le. Dans la figure ci-dessus, lors du calcul de Fib Dans le processus (5), Fib(1) a été calculé deux fois, Fib(2) a été calculé trois fois et Fib(3) a été calculé deux fois. La tâche qui ne nécessitait à l'origine que 5 calculs a été calculée. 9 fois. Ce problème deviendra de plus en plus important à mesure que l’échelle augmente, de sorte que Fib(1000) ne pourra plus être calculé dans un délai acceptable.

Ce que nous utilisions à cette époque était simplement d'utiliser la définition pour trouver fib(n), c'est-à-dire d'utiliser la formule fib(n) = fib(n-1) fib(n-2). Il est facile de penser à cette idée, mais après une analyse minutieuse, nous constatons que lorsque fib(n-1) est appelé, fib(n-2) est également appelé, ce qui signifie que fib(n-2) est appelé deux fois. de la même manière, f(n-3) est également appelé deux fois lorsque f(n-2) est appelé, et ces appels redondants sont totalement inutiles. On peut calculer que la complexité de cet algorithme est exponentielle.

Algorithme récursif de Fibonacci amélioré

Existe-t-il donc un meilleur algorithme récursif pour calculer la séquence de Fibonacci ? Bien sûr, il y en a. Jetons un coup d'œil aux premiers nombres de Fibonacci :

11, 1, 2, 3, 5, 8, 13, 21, 34, 55…

Avez-vous remarqué, si nous le faisions ? supprimez l'élément précédent, la séquence résultante satisfait toujours f(n) = f(n-1) – f(n-2), (n>2), et la séquence que nous obtenons commence par 1, 2 . Il est facile de constater que le n-1ème élément de cette séquence est le nème élément de la séquence d’origine. Et si, savez-vous comment nous devrions concevoir l’algorithme ? Nous pouvons écrire une telle fonction, qui accepte trois paramètres, les deux premiers sont les deux premiers éléments de la séquence et le troisième est le numéro de la séquence que nous voulons trouver en commençant par les deux premiers paramètres.

1int fib_i(int a, int b, int n);

Dans la fonction, nous vérifions d'abord la valeur de n Si n est 3, il nous suffit de renvoyer a b. est une situation simple. Si n>3, alors nous appelons f(b, a b, n-1), afin de réduire la taille du problème (de la recherche du nième élément à la recherche du n-1ème élément). D'accord, le code final est le suivant :

int fib_i(int a, int b , int n)
{
    if(n == 3)
        return a+b;
    else
        return fib_i(b, a+b, n-1);
}

Pourquoi y a-t-il une surcharge de mémoire importante ?

Le principe de la récursion est le suivant : stockez d'abord la valeur de la variable à calculer sur la pile, puis bouclez en séquence jusqu'à ce que la condition de fin de récursion soit remplie, puis prenez la valeur de la variable à calculer à partir de la pile et calculez le résultat final. .
Une analogie : Calculez 10 ! =
Pour la récursivité, le processus est : 10 ! =10 * 9 !
9 !=9 * 8 !
……
2 ! =2*1 !
1 ! =1
Lors du calcul, il stocke les expressions en mémoire une par une jusqu'à ce que la condition de récursion satisfasse 1 ! =1, puis récupérez l'expression qui vient d'être enregistrée dans la mémoire pour obtenir le résultat final. Dans ce cas, davantage de ressources système seront dépensées.

Et le système définira la profondeur de récursion maximale. Si elle est supérieure à cette profondeur, une erreur sera signalée et quittée. Lors de l'appel récursif d'une fonction, les paramètres, les valeurs de retour, etc. de la fonction seront continuellement poussés sur la pile. Les appels de fonction utiliseront constamment la pile, rapporteront et restaureront la scène, de sorte que la surcharge de mémoire deviendra de plus en plus importante. La solution est la récursion de queue. Cependant, PHP n'a aucun effet d'optimisation sur la récursion de queue, donc cette solution n'a pas d'importance pratique.