Maison >développement back-end >tutoriel php >Programmation dynamique d'apprentissage d'algorithmes PHP (2)
Programmation dynamique d'apprentissage d'algorithmes PHP (2)
- 黄舟original
- 2017-02-06 09:56:592235parcourir
J'ai brièvement présenté le concept et les étapes de solution de la programmation dynamique auparavant, mais au cours de mon étude, j'ai senti que le champ d'application de la programmation dynamique était trop flexible. Ici, je vais choisir quelques questions courantes et m'entraîner davantage.
1. Sous-séquence commune la plus longue (liée à la chaîne)
Étant donné deux chaînes, trouvez la sous-séquence commune (LCS) la plus longue et renvoyez la longueur de LCS. Par exemple :
Par exemple : étant donné "ABCD" et "EDCA", le LCS est "A" (ou D ou C), renvoie 1
étant donné "ABCD" et "EACB", le LCS est " ; AC" renvoie 2.
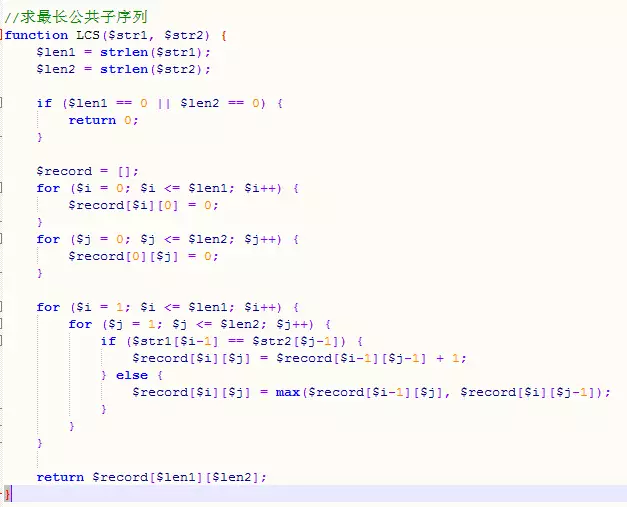
Idée : Chaîne a de longueur m et chaîne b de longueur n, leur plus longue sous-séquence commune la plus longue[m][n] peut être passée par a et n-1 de longueur m-1 La longueur b est déduite : lorsque a[m] est égal à b[n], le plus long[m][n] = le plus long[m-1][n-1] 1; lorsque a[m] n'est pas égal à b[n ], le plus long [m][n]=max(le plus long[m-1][n], le plus long[m][n-1]). Lorsque la chaîne a ou b est une chaîne vide, la sous-séquence commune la plus longue entre elle et l'autre chaîne doit être 0. La solution à la dernière question est la plus longue[strlen(a)][strlen(b)].
Code :
2. Modifier la distance (liée à la chaîne)
Étant donné deux mots mot1 et mot2, calculez mot1 pour obtenir le nombre minimum d'opérations pour mot2.
Vous disposez de trois méthodes de fonctionnement au total : insérer un caractère, supprimer un caractère et remplacer un caractère.
Par exemple : étant donné work1="mart" et work2="karma", renvoie 3.
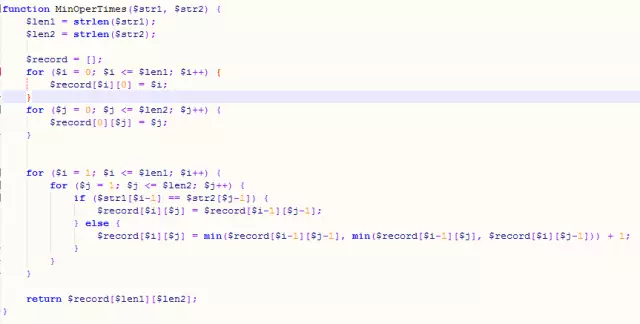
Idée : Pour une chaîne a de longueur m et une chaîne b de longueur n (m et n sont tous deux supérieurs à 0), si a[m] n'est pas égal à b[n], alors a devient b Le nombre minimum d'opérations = min(a[m-1] devient le nombre minimum d'opérations de b[n] 1, a[m] devient le nombre minimum d'opérations de b[n-1] 1, a[m -1] devient est le nombre minimum d'opérations pour b[n-1]); si a[m] est égal à b[n], alors le nombre minimum d'opérations pour que a[m] devienne b[n] = a[m-1] devient b[ n-1] nombre minimum d'opérations.
Code :
3. Problème de sac à dos
Étant donné le volume A[i] et sa valeur V[i] de n articles, Ils mettent dans un sac à dos de taille m, quelle est la valeur totale maximale qu'on peut y mettre ?
Par exemple : pour le volume de l'article [2, 3, 5, 7] et la valeur correspondante [1, 5, 2, 4], en supposant que la taille du sac à dos est de 10, la valeur maximale pouvant être chargée est de 9.
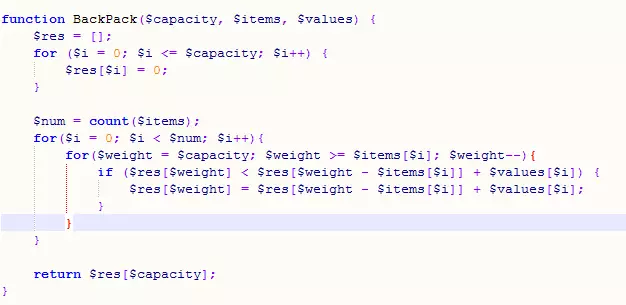
Idée : Lorsque l'espace est v, pour tout élément i, si i peut être mis dedans (v est supérieur ou égal au poids[i]), alors la valeur f(v) de l'espace v à ce moment est égal aux valeurs f(v -weight[i])[i], donc en parcourant tous les éléments, vous pouvez trouver la valeur maximale qui peut être obtenue lorsque l'espace est v.
Code :
4. Problème d'intervalle (question d'entretien Google)
Il y a n pièces alignées dans une ligne, chaque pièce a une valeur différente. valeur. Les deux concurrents prennent à tour de rôle une pièce de chaque côté jusqu'à ce qu'il ne reste plus de pièce. La valeur totale des pièces obtenues est calculée et celle avec la valeur la plus élevée gagne. Veuillez décider si le premier joueur perd ou gagne ?
Par exemple : étant donné le tableau [3,2,2], renvoie vrai ; étant donné le tableau [1,20,15], renvoie faux.
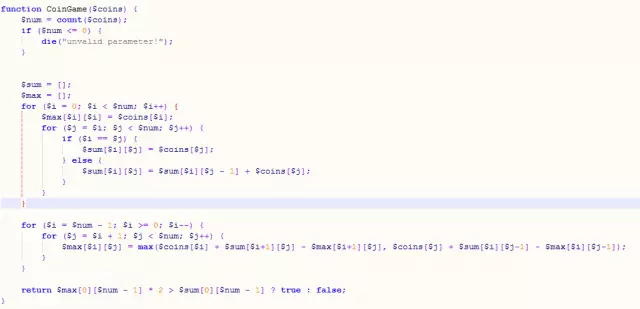
Idée : Pour un intervalle fermé donné (i à j, j est supérieur ou égal à i), le joueur A n'a que deux façons de prendre la pièce, par la gauche ou par la droite. Si vous le prenez par la gauche, la valeur nominale maximale que A peut obtenir = la valeur nominale totale de la plage restante de la valeur nominale de la pièce que vous obtenez - la valeur nominale maximale que le joueur B peut obtenir dans la plage restante ; la situation où A le prend par la droite est différente de la situation où A le prend par la gauche est similaire. À partir de là, nous pouvons obtenir l’équation de transition d’état. Grâce à deux boucles, nous pouvons obtenir la valeur nominale totale de n'importe quel intervalle de i à j dans la séquence de longueur n, ainsi que la valeur maximale obtenue par le premier joueur lorsque j=i (c'est-à-dire la valeur nominale du i -ème pièce).
Code :
Ce qui précède est le contenu de l'algorithme PHP d'apprentissage de la programmation dynamique (2). Pour plus de contenu connexe, veuillez faire attention au site Web PHP chinois (www). .php.cn ) !
Articles Liés
Voir plus- Comment utiliser cURL pour implémenter les requêtes Get et Post en PHP
- Comment utiliser cURL pour implémenter les requêtes Get et Post en PHP
- Comment utiliser cURL pour implémenter les requêtes Get et Post en PHP
- Comment utiliser cURL pour implémenter les requêtes Get et Post en PHP
- Tous les symboles d'expression dans les expressions régulières (résumé)

